Guida alla Conversione da Numero Decimale a Frazione
Convertire un numero decimale in una frazione è un’operazione semplice e veloce da eseguire. Se hai bisogno di capire come fare, segui attentamente le istruzioni riportate in questo articolo. In caso contrario, se stai cercando di convertire una frazione in un numero decimale, consulta l’apposito articolo. Ricorda che, anche se i due metodi potrebbero sembrare difficili inizialmente, con un po’ di pratica diventeranno sempre più semplici da eseguire. In questo modo, sarai in grado di eseguire la conversione da decimale a frazione in modo preciso e veloce, senza incontrare alcuna difficoltà.

Come Convertire un Numero Decimale Finito in Frazione
Passo 1: Prendere nota del numero decimale da convertire
Prima di iniziare la conversione di un numero decimale finito in frazione, è necessario identificare il numero da convertire. Ad esempio, se si deve convertire il numero decimale 0,325, prendere nota di tale valore.
Passo 2: Convertire il numero decimale in una frazione
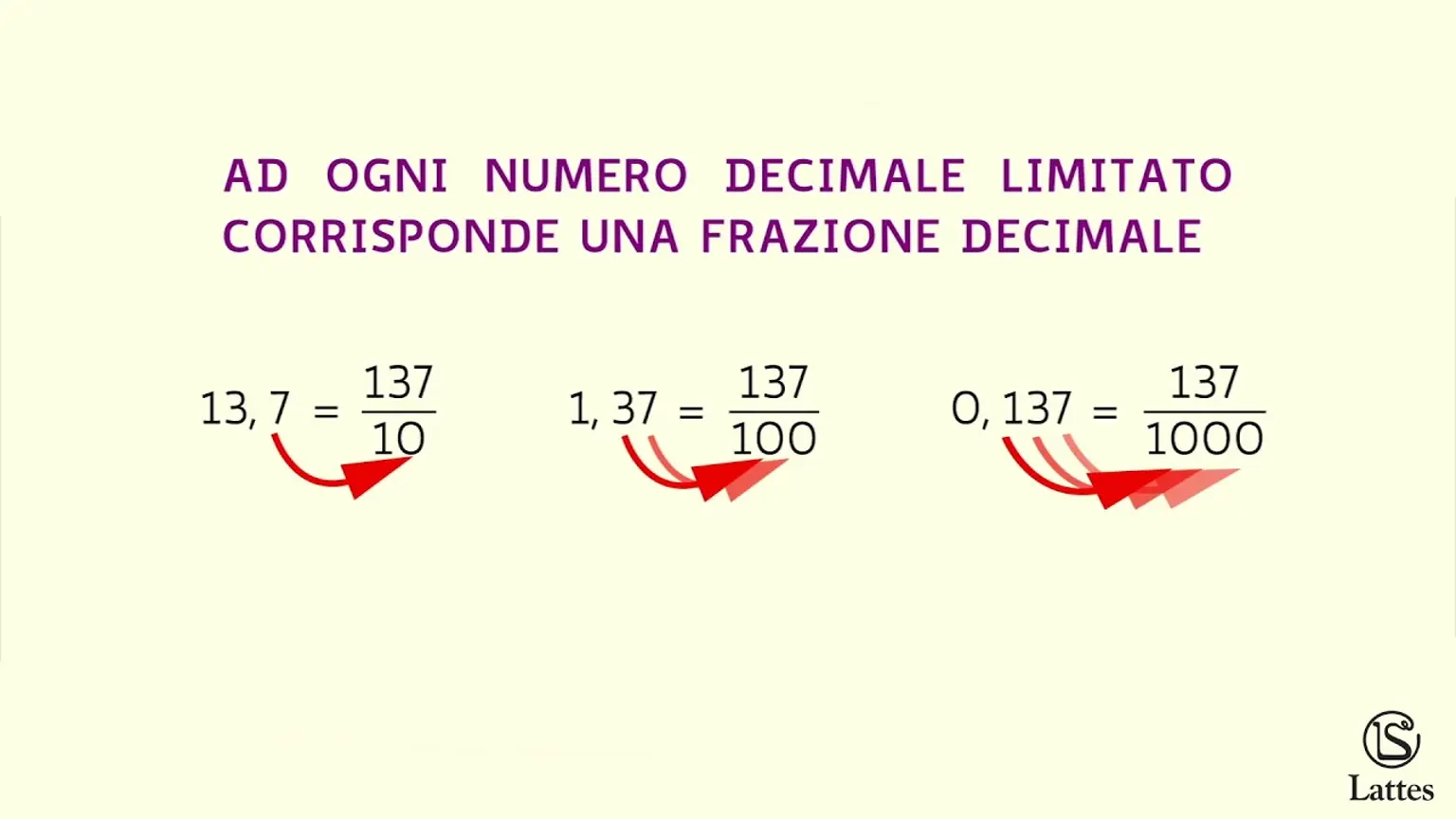
Per convertire il numero decimale in una frazione, è necessario contare le cifre presenti dopo il separatore decimale e utilizzarle come numeratore della frazione. Nel caso del numero decimale 0,325, esso è composto da tre cifre decimali. Pertanto, il numeratore della frazione sarà 325, mentre il denominatore sarà 1.000. Questo significa che il numero decimale 0,325 può essere rappresentato come la frazione 325/1.000.
Forma letterale
In alternativa, è possibile esprimere il risultato finale in forma letterale. Nel nostro esempio, il numero decimale 0,325 corrisponde a “325 millesimi”. Anche così, si sta indicando una frazione, dato che 0,325 è uguale a 325/1.000.

Passo 3: Individuare il massimo comune multiplo del numeratore e del denominatore della frazione
Per semplificare il risultato finale, è necessario individuare il massimo comune multiplo del numeratore e del denominatore della frazione. Nel caso della frazione 325/1.000, il massimo comune multiplo è 25, dato che è il divisore più grande che produce come risultato un valore intero. Questo significa che è possibile semplificare la frazione dividendo numeratore e denominatore per 25.
Da numero decimale a frazione – YouTube
Approccio alternativo
In alternativa, è possibile semplificare la frazione adottando un approccio più pratico e andando per tentativi. Ad esempio, se la frazione è composta da due numeri pari, si possono continuare a dividerli entrambi per 2 finché non si ottiene come risultato un numero dispari o finché non si è più in grado di semplificare ulteriormente la frazione. Se la frazione è composta da numeri dispari, si può provare a dividerli per 3. Se la frazione è composta da numeri che terminano con 0 o 5, è possibile dividerli per il numero 5.
Passo 4: Semplificare la frazione
Una volta individuato il massimo comune multiplo, è possibile semplificare la frazione dividendo numeratore e denominatore per tale valore. Nel nostro esempio, il numeratore 325 diviso per il massimo comune multiplo 25 produce come risultato 13, mentre il denominatore 1.000 diviso per 25 produce come risultato 40. Pertanto, il risultato finale della conversione del numero decimale 0,325 in frazione è 13/40. In altre parole, è possibile affermare che 0,325 è ugule a 13/40.
Riassunto
Per convertire un numero decimale finito in frazione, è necessario seguire i seguenti passaggi:
Prendere nota del numero decimale da convertire.
Convertire il numero decimale in una frazione, utilizzando le cifre dopo il separatore decimale come numeratore e 1.000 come denominatore.
Individuare il massimo comune multiplo del numeratore e del denominatore della frazione, in modo da semplificare il risultato finale.
Semplificare la frazione dividendo numeratore e denominatore per il massimo comune multiplo.
Seguendo questi passaggi, sarà possibile convertire qualsiasi numero decimale finito in frazione, semplificando il risultato finale per ottenere una rappresentazione più agevole e intuitiva del numero stesso.
Come Convertire un Numero Decimale Periodico in Frazione
Passo 1: Prendere nota del numero da convertire
Per convertire un numero decimale periodico in frazione, è necessario prendere nota del numero da convertire. Un numero decimale periodico è composto da una sequenza di cifre decimali che si ripete all’infinito. Ad esempio, il numero 2,345454545 è un numero decimale periodico.
Passo 2: Moltiplicare per la potenza di dieci
Per convertire il numero decimale periodico in frazione, è necessario moltiplicare il numero per la potenza di dieci necessaria per spostare a sinistra del separatore decimale tutte le cifre decimali che non si ripetono. Nell’esempio precedente, è sufficiente usare una sola potenza di 10 ottenendo come risultato “10x = 23,45454545…”, dato che l’unica cifra decimale che non si ripete è il 3.
Passo 3: Moltiplicare per un’altra potenza di dieci
Successivamente, moltiplicare entrambi i membri dell’equazione per un’altra potenza di dieci per spostare più cifre dalla parte decimale alla parte intera del numero da convertire. In questo caso, ipotizziamo di moltiplicare il numero decimale di partenza per 1.000 ottenendo la seguente equazione “1.000x = 2.345,45454545…”.

Passo 4: Incolonnare le equazioni
Incolonnare le due equazioni ottenute in modo che i membri di sinistra e di destra siano allineati fra loro. In questo modo, è possibile eseguire la sottrazione dei rispettivi valori. Nell’esempio precedente, posiziona la seconda equazione sopra alla prima, cioè 1.000x = 2.345,45454545 sopra a 10x = 23,45454545.
Passo 5: Eseguire i calcoli
Eseguire i calcoli. Sottrarre il valore 10x da 1.000x ottenendo come risultato 990x, quindi sottrarre il numero 23,45454545 da 2.345,45454545 per ottenere come valore 2.322. L’equazione finale è la seguente 990x = 2.322.
Passo 6: Risolvere l’equazione
Risolvi l’equazione in base alla variabile “x”. Dividi entrambi i membri per il numero 990 ottenendo come risultato x = 2.322/990.
Passo 7: Semplificare la frazione
Semplifica la frazione che hai ottenuto. Individua il massimo comune divisore del numeratore e del denominatore della frazione che hai ottenuto come risultato. Dividi il numeratore e il denominatore per uno qualsiasi dei fattori comuni. Nel nostro esempio, il massimo comune divisore di 2.322 e 990 è 18, quindi dividendo 990 e 2.322 per 18 otterrai 990/18 = 129 e 2.322/18 = 55. A questo punto, il risultato finale della conversione è la frazione 129/55, che può essere semplificata ulteriormente dividendo sia il numeratore che il denominatore per il loro massimo comune divisore, ovvero 3. La frazione semplificata sarà quindi 43/18.
Riassunto
Per convertire un numero decimale periodico in frazione, è necessario seguire i seguenti passaggi:
- Prendere nota del numero da convertire.
- Moltiplicare il numero da convertire per la potenza di dieci necessaria per spostare a sinistra del separatore decimale tutte le cifre decimali che non si ripetono.
- Moltiplicare entrambi i membri dell’equazione per un’altra potenza di dieci per spostare più cifre dalla parte decimale alla parte intera del numero da convertire.
- Incolonnare le due equazioni ottenute in modo che i membri di sinistra e di destra siano allineati fra loro.
- Eseguire la sottrazione dei rispettivi valori.
- Risolvere l’equazione in base alla variabile “x”.
- Semplificare la frazione che hai ottenuto.
Seguendo questi passaggi, sarà possibile convertire qualsiasi numero decimale periodico in frazione, semplificando il risultato finale per ottenere una rappresentazione più agevole e intuitiva del numero stesso.
Consigli per la Conversione di Numeri Decimali in Frazioni
Praticare il Metodo
Come per molte altre cose, la pratica rende perfetti anche per la conversione di numeri decimali in frazioni. Una volta acquisita familiarità con il metodo, risolvere questo tipo di problemi matematici richiederà solo pochi secondi, a meno che non sia necessario semplificare il risultato finale.
Prepararsi con il Necessario
Se stai affrontando questo tipo di conversione per la prima volta, è consigliabile avere a portata di mano un foglio di carta su cui prendere appunti e registrare i risultati intermedi, insieme ad una gomma per cancellare eventuali errori di calcolo.
Controllare i Risultati
Controllare sempre che il risultato finale sia corretto. Ad esempio, l’equazione “2 5/8 = 2,375” sembra corretta, mentre se come risultato finale ottenessi “32/1.000 = 0,50”, sarebbe evidente che hai commesso degli errori di calcolo.
Avvertenze
Semplificare la Frazione
Semplificare sempre la frazione finale usando i valori corretti. Non è sufficiente dividere il numeratore e il denominatore per il primo valore che ti viene in mente. È necessario individuare il massimo comune divisore e utilizzarlo per semplificare la frazione in modo corretto.
In sintesi, per convertire numeri decimali in frazioni, è importante esercitarsi, prepararsi con il necessario, controllare i risultati e semplificare la frazione finale in modo corretto per ottenere una rappresentazione più chiara e intuitiva del numero.
Stai guardando: Guida alla Conversione da Numero Decimale a Frazione