CIRCONFERENZA

La circonferenza nel piano cartesiano è un insieme di punti che si trovano alla stessa distanza da un punto fisso chiamato centro della circonferenza. La sua equazione generale è data da (x-xC)2+(y-yC)2=r2, dove xC e yC sono le coordinate del centro e r è il raggio della circonferenza. È importante notare che una circonferenza è una conica non degenere.

In questa lezione, ci concentreremo sulle formule per la circonferenza nel piano cartesiano, senza trattare formule per il cerchio o la circonferenza come l’area e il perimetro, che sono state già trattate in un’altra lezione di Geometria piana. Esploreremo le possibili forme dell’equazione della circonferenza, le formule per calcolare le coordinate del centro e il raggio della circonferenza, e altre formule utili.
Circonferenza nel piano cartesiano
Definizione di circonferenza
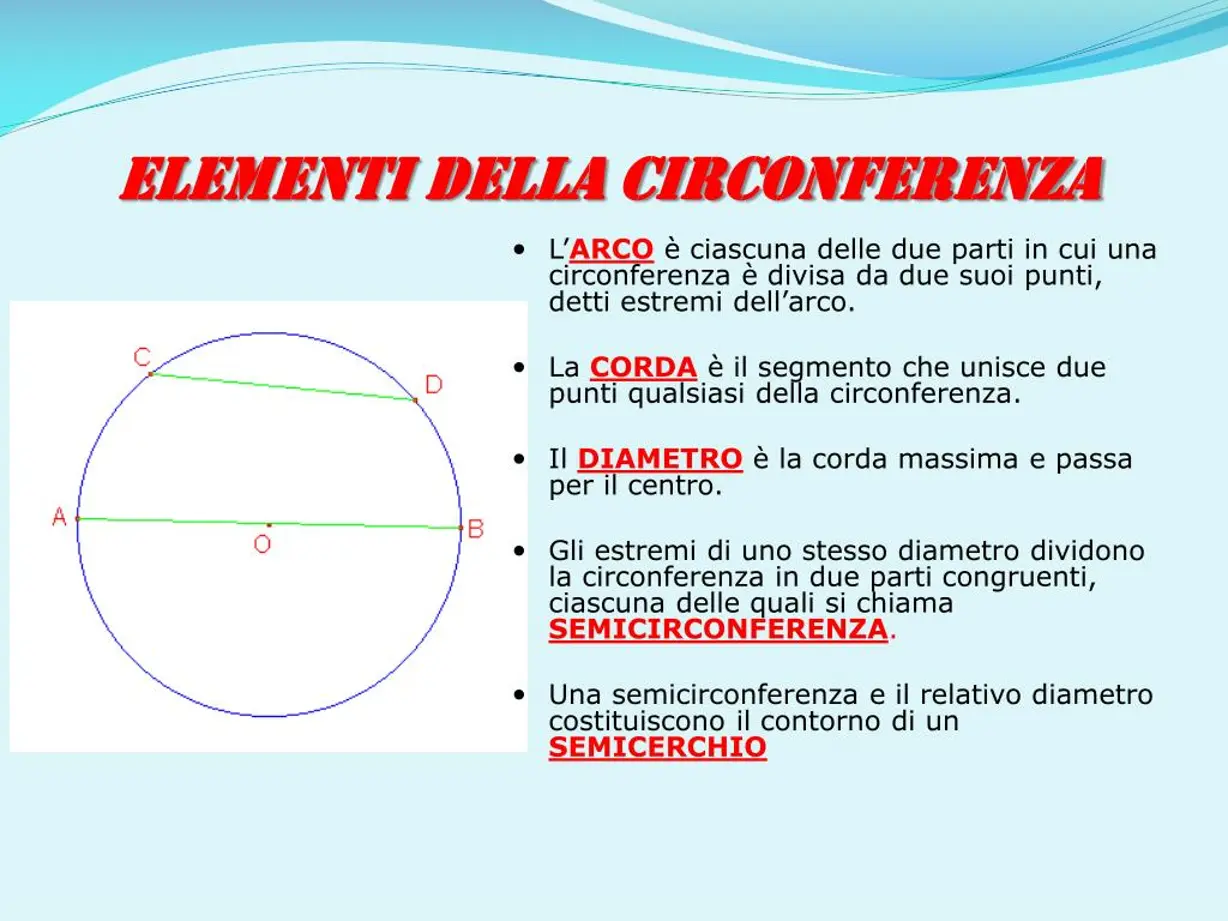
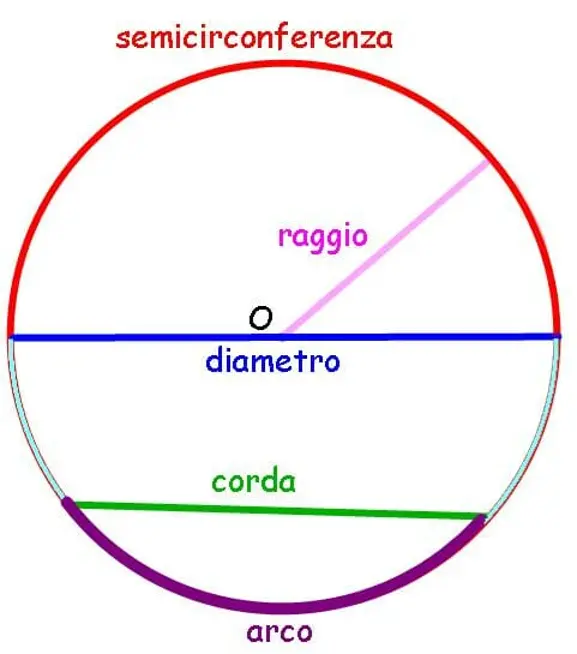
In geometria, la circonferenza è il luogo geometrico dei punti P del piano equidistanti da un punto C, chiamato centro della circonferenza. Il raggio di una circonferenza è la distanza di qualsiasi punto della circonferenza dal centro, solitamente indicata con r, quindi ogni punto della circonferenza soddisfa la condizione CP = r.
Definizione di cerchio
Il cerchio è la regione dei punti del piano interni alla circonferenza. In altre parole, il cerchio è il luogo geometrico dei punti che distano meno del raggio r dal centro della circonferenza.
È possibile rappresentare una circonferenza sul piano cartesiano mediante un sistema di coordinate cartesiane. La formula generale dell’equazione di una circonferenza di centro (a, b) e raggio r è:
(x – a)² + (y – b)² = r²
dove x e y rappresentano le coordinate del punto P sulla circonferenza. Questa equazione può essere utilizzata per determinare l’equazione di una circonferenza a partire dal suo centro e dal suo raggio.
Formule della circonferenza
Circonferenza : equazione e rappresentazione nel piano cartesiano – YouTube
Equazione della circonferenza noti centro e raggio
In geometria analitica, le formule per la circonferenza nel piano cartesiano ampliano quelle già note dallo studio della geometria euclidea. È possibile esprimere l’equazione della circonferenza conoscendo le coordinate del centro della circonferenza (xC, yC) e il raggio r, nella forma:
(x – xC)² + (y – yC)² = r²
Questa equazione rappresenta un’equazione di secondo grado in due incognite x e y, dove un punto (x, y) appartiene alla circonferenza se e solo se le sue coordinate cartesiane soddisfano l’equazione della circonferenza.
Nel caso in cui la circonferenza abbia centro nell’origine degli assi O = (0,0) e raggio r, l’equazione della circonferenza si riduce a:
x² + y² = r²
Equazione canonica della circonferenza
L’equazione canonica della circonferenza è un’equazione quadratica in due incognite x e y che viene espressa in forma implicita, con secondo membro uguale a zero. L’equazione si presenta come:
x² + y² + αx + βy + γ = 0
dove il primo membro è un polinomio di secondo grado nelle incognite x e y e coefficienti numerici α, β, γ. Questa equazione è utile per determinare le proprietà della circonferenza, come il raggio, il centro e l’intersezione con altre circonferenze.
Relazioni e formule di passaggio tra le equazioni della circonferenza
In geometria analitica, ci sono due forme di equazioni per la circonferenza: l’equazione noti centro e raggio e l’equazione canonica. È possibile passare da una forma all’altra utilizzando relazioni e formule di passaggio.
Relazioni tra le due equazioni
Per passare dall’equazione noti centro e raggio all’equazione canonica, si può utilizzare la regola per il quadrato del binomio. Dopo aver sviluppato il quadrato del binomio nella prima forma, confrontiamo i coefficienti con la seconda forma. In questo modo, si possono ricavare le relazioni tra i coefficienti:
α = -2xC, β = -2yC, γ = xC² + yC² – r²
D’altra parte, partendo dall’equazione della circonferenza nella forma canonica, è possibile calcolare le coordinate del centro della circonferenza e la misura del raggio usando le seguenti formule:
C = (-(α)/(2), -(β)/(2)) ; r = √((α²)/(4) + (β²)/(4) – γ)
Metodo del completamento dei quadrati
Un’alternativa per passare dall’equazione canonica all’equazione noti centro e raggio consiste nell’applicare il metodo del completamento dei quadrati. Questo metodo richiede di completare i quadrati delle incognite x e y e di ottenere l’equazione nella forma noti centro e raggio.
Raggio conoscendo il centro e un punto della circonferenza
Il raggio di una circonferenza può essere calcolato con facilità se conosciamo le coordinate del centro C = (xC, yC) e un punto P = (xP, yP) appartenente alla circonferenza. In tal caso, la misura del raggio è data dalla formula:
r = √((xP – xC)² + (yP – yC)²)
Cerchio nel piano cartesiano
Un cerchio può essere descritto nel piano cartesiano attraverso l’equazione della circonferenza che lo delimita. Se disponiamo dell’equazione della circonferenza, possiamo individuare tutti e soli i punti interni o esterni alla circonferenza. Ad esempio, per individuare la regione dei punti interni alla circonferenza data dall’equazione:
(x – xC)² + (y – yC)² = r²
possiamo scrivere la disequazione:
(x – xC)² + (y – yC)² < r²
Se invece l’equazione è in forma canonica:
x² + y² + αx + βy + γ = 0
la disequazione diventa:
x² + y² + αx + βy + γ < 0
Per individuare la regione dei punti esterni alla circonferenza, occorre scrivere una delle seguenti disequazioni:
(x – xC)² + (y – yC)² > r² ; x² + y² + αx + βy + γ > 0
Circonferenza passante per tre punti non allineati
Esistono due modi per individuare univocamente una circonferenza nel piano cartesiano. Il primo prevede di conoscere le coordinate del centro e la misura del raggio; il secondo si basa sul noto teorema della Geometria Euclidea, il quale afferma che per tre punti non allineati passa una ed una sola circonferenza.
Pertanto, conoscendo le coordinate di tre punti non allineati, ovvero tali da non giacere su una stessa retta, è possibile trovare l’unica circonferenza che li contiene.
Posizioni tra circonferenza e retta
Esistono diverse posizioni tra una circonferenza e una retta nel piano cartesiano. È possibile analizzare tali posizioni dal punto di vista geometrico ed analitico. Per ulteriori informazioni, consultare il formulario dedicato alle posizioni tra circonferenza e retta.
Fonte del contenuto: youmath.it
Circonferenze e rette nel piano cartesiano
Definizione di circonferenza e cerchio
Si definisce circonferenza il luogo geometrico dei punti P del piano equidistanti da un punto C, detto centro della circonferenza. La distanza di un qualsiasi punto della circonferenza dal centro è detta raggio e viene solitamente indicata con r, cosicché tutti i punti della circonferenza soddisfano la condizione CP = r. Data una circonferenza, si definisce cerchio la regione dei punti del piano interni alla circonferenza.
Formule della circonferenza
Le formule per la circonferenza nel piano cartesiano ampliano le formule per cerchio e circonferenza già note dallo studio della Geometria Euclidea. L’equazione della circonferenza noti centro e raggio è (x-x_C)^2+(y-y_C)^2 = r^2, mentre l’equazione canonica della circonferenza è x^2+y^2+α x+β y+γ = 0.
Relazioni e formule di passaggio tra le equazioni della circonferenza
Le relazioni tra l’equazione della circonferenza noti centro e raggio e l’equazione canonica della circonferenza si ricavano usando la regola per il quadrato del binomio e confrontando i coefficienti. È possibile calcolare le coordinate del centro della circonferenza e la misura del raggio partendo dall’equazione della circonferenza nella forma canonica usando le formule. Inoltre, se disponiamo delle coordinate del centro e di un punto P appartenente alla circonferenza, possiamo calcolare la misura del raggio usando la formula per la distanza tra due punti.
Posizioni tra circonferenza e retta
La posizione di una retta rispetto ad una circonferenza può essere analizzata nel dettaglio dal punto di vista geometrico ed analitico. In particolare, se vogliamo calcolare l’equazione della retta tangente ad una circonferenza in un suo punto, possiamo usare la formula di sdoppiamento. L’asse centrale di due circonferenze è la retta passante per i loro centri, mentre l’asse radicale di due circonferenze secanti è la retta passante per i due punti di intersezione delle due circonferenze e perpendicolare all’asse centrale. L’equazione dell’asse radicale può essere determinata usando la formula (α-α’)x+(β-β’)y+γ-γ’= 0. Nel caso limite di due circonferenze tangenti, l’asse radicale si riduce alla retta perpendicolare all’asse centrale e passante per il punto di tangenza, mentre per qualsiasi altra posizione tra le due circonferenze l’asse radicale non esiste.
Stai guardando: CIRCONFERENZA