CONVERTIRE I GRADI IN RADIANTI E VICEVERSA
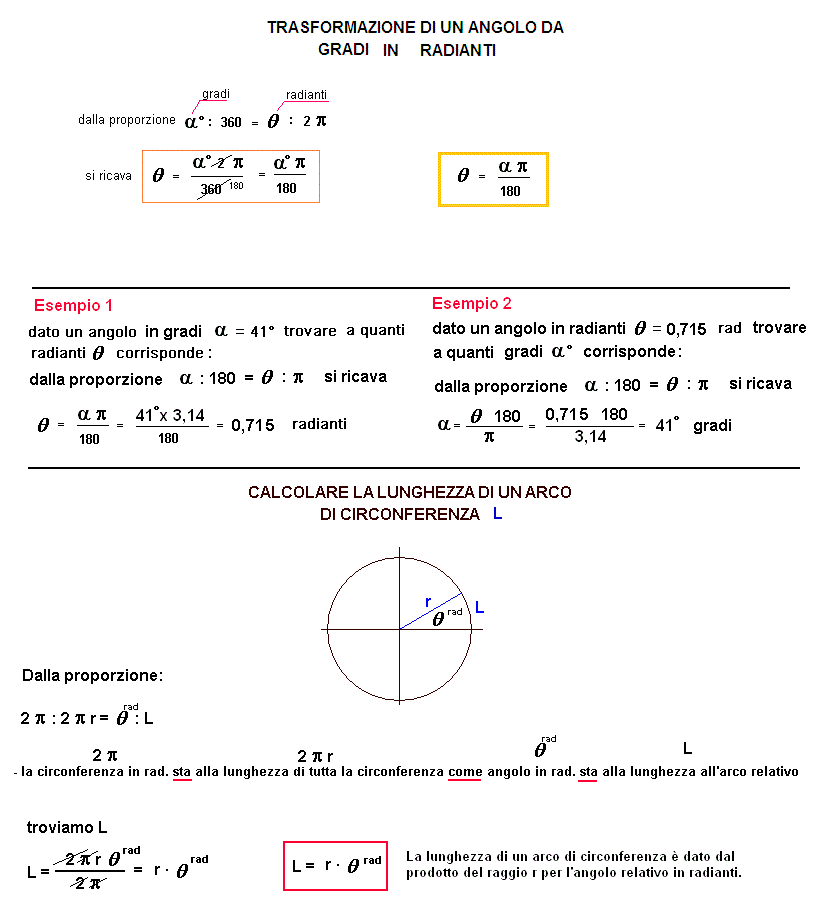
La conversione tra gradi e radianti è un processo matematico che permette di esprimere la misura di un angolo in una delle due unità di misura utilizzate. Poiché la comprensione della misura degli angoli è fondamentale per la trigonometria, dedicare del tempo a questo argomento propedeutico è essenziale.

Anche se la misura degli angoli viene introdotta alle scuole medie, è importante ricordare che tale conoscenza viene richiesta nuovamente nella trigonometria e, pertanto, non va sottovalutata. Grazie alle semplici operazioni algebriche che permettono la conversione tra gradi e radianti, è possibile effettuare calcoli e risolvere problemi trigonometrici con maggiore facilità.
Come passare dai gradi ai radianti, e viceversa
Nella goniometria, l’angolo è l’unità di misura principale, utilizzata per descrivere la rotazione di un oggetto intorno a un punto fisso. Esistono due tipi di misure di angolo: i gradi e i radianti, entrambi utilizzati sia nelle applicazioni pratiche che per le questioni teoriche.
Passaggio dai gradi ai radianti
Per passare dai gradi ai radianti, possiamo utilizzare la seguente formula:
Formula:
r^(rad) = (g°×π^(rad))/(180°)
dove g° rappresenta la misura di un angolo espressa in gradi e r^(rad) rappresenta la stessa misura espressa in radianti.
Per esempio, se abbiamo un angolo di 60° e vogliamo convertirlo in radianti, possiamo utilizzare la formula come segue:
r^(rad) = (60°×π^(rad))/(180°) = π^(rad)/3
Quindi, l’angolo di 60° corrisponde a π^(rad)/3 radianti.
È importante notare che la formula per la conversione dai gradi ai radianti prevede che la misura in gradi sia espressa sotto forma di numero decimale. Pertanto, per convertire le misure in gradi, primi e secondi, con primi e secondi non nulli, andranno espresse come misura decimale in gradi. In questo senso si può ricorrere alla formula:
Misura Degli Angoli in GRADI e RADIANTI: conversione da gradi a radianti e viceversa – YouTube
Formula:
misura decimale in gradi = gradi+(primi)/(60)+(secondi)/(3600)
che deriva direttamente dalla definizione di sistema sessagesimale: 60 secondi formano un primo, 60 primi formano un grado.
Passaggio dai radianti ai gradi
Per passare dai radianti ai gradi, possiamo utilizzare la seguente formula:
Formula:
g° = (r^(rad)×180°)/(π^(rad))
Quindi, se abbiamo un angolo di π^(rad)/3 radianti e vogliamo convertirlo in gradi, possiamo utilizzare la formula come segue:
g° = (π^(rad)/3×180°)/(π^(rad)) = 60°
Quindi, l’angolo di π^(rad)/3 radianti corrisponde a 60°.
È importante ricordare che la conversione tra gradi e radianti è una operazione fondamentale per la risoluzione degli esercizi in goniometria, quindi è necessario essere in grado di gestire e convertire queste misure con facilità.
Esempi di conversione dai gradi ai radianti e dai radianti ai gradi
Nella goniometria, spesso ci troveremo a dover convertire le misure di angolo da una unità di misura all’altra. Ecco di seguito due esempi di conversione dai gradi ai radianti e dai radianti ai gradi.
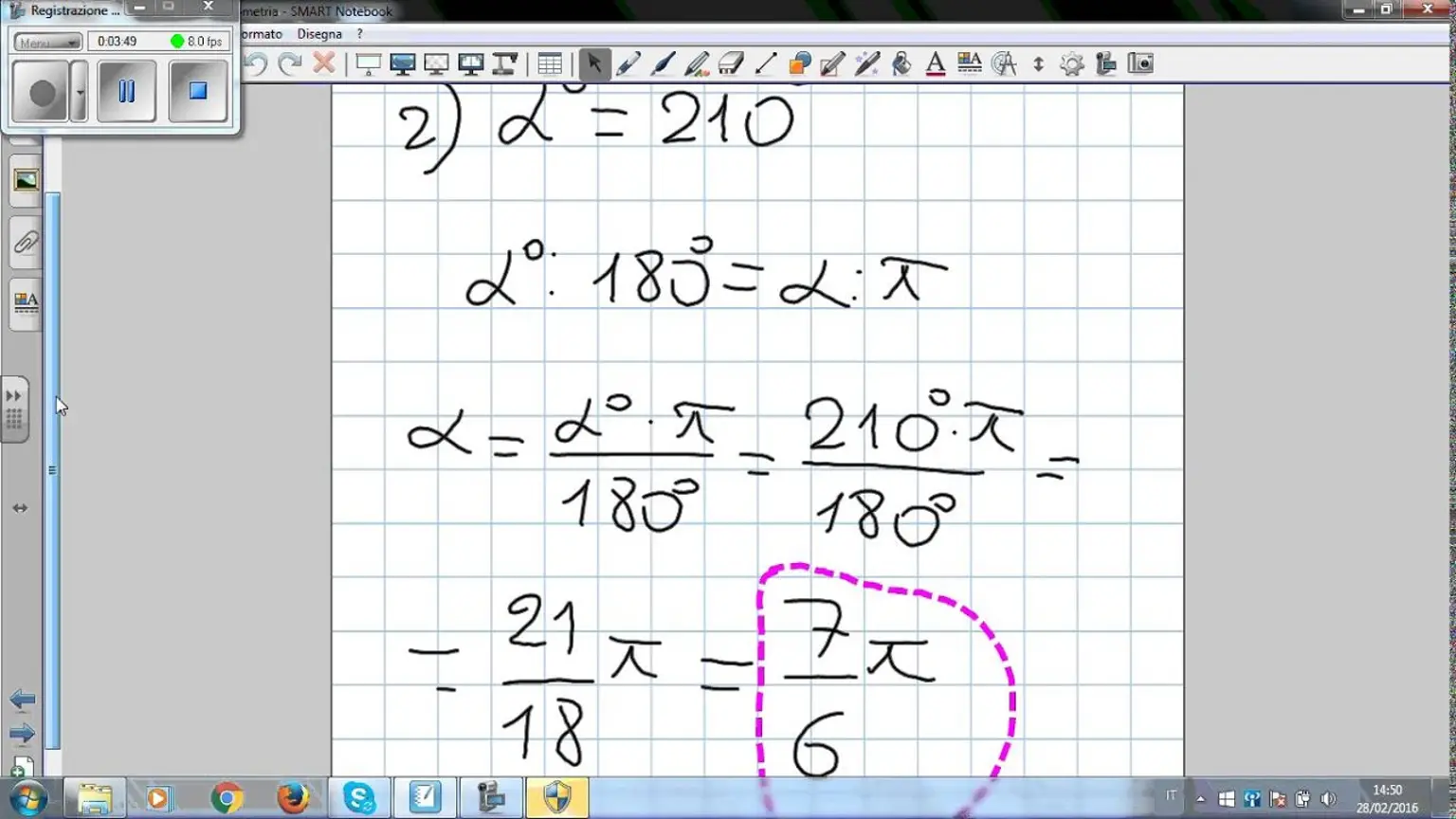
Esempio 1: conversione da radianti a gradi
Vogliamo esprimere 1 radiante in gradi.
Svolgimento:
Utilizziamo la formula:
Formula:
g° = (r^(rad)×180°)/(π^(rad))
Quindi, sostituendo i valori:
(1^(rad)×180°)/(π^(rad)) ≃ 57.2958°
A questo punto possiamo esprimere la misura in gradi che abbiamo ottenuto in forma normale (se non ricordate come procedere, date un’occhiata alla lezione sulla misura degli angoli in forma normale e su gradi, primi e secondi).
57.2958° → 57° , 17′ , 44.8”
Esempio 2: conversione da gradi a radianti
Supponiamo ora di voler esprimere in radianti la misura 30° , 15′ , 30”.
Svolgimento:
Per prima cosa scriviamo la misura in gradi in forma di numero decimale:
Formula:
misura decimale in gradi = gradi+(primi)/(60)+(secondi)/(3600)
30° , 15′ , 30”= 30°+((15)/(60))°+((30)/(3600))° = 30.2583°
Dopodiché utilizziamo la relazione:
Formula:
r^(rad) = (g°×π^(rad))/(180°)
Sostituendo i valori:
(30.2583°×π^(rad))/(180°) = 0.528107 rad
Quindi, la misura di 30° , 15′ , 30” corrisponde a 0.528107 radianti.
È importante ricordare che la conversione tra gradi e radianti è una operazione fondamentale per la risoluzione degli esercizi in goniometria, quindi è necessario essere in grado di gestire e convertire queste misure con facilità.
Stai guardando: CONVERTIRE I GRADI IN RADIANTI E VICEVERSA