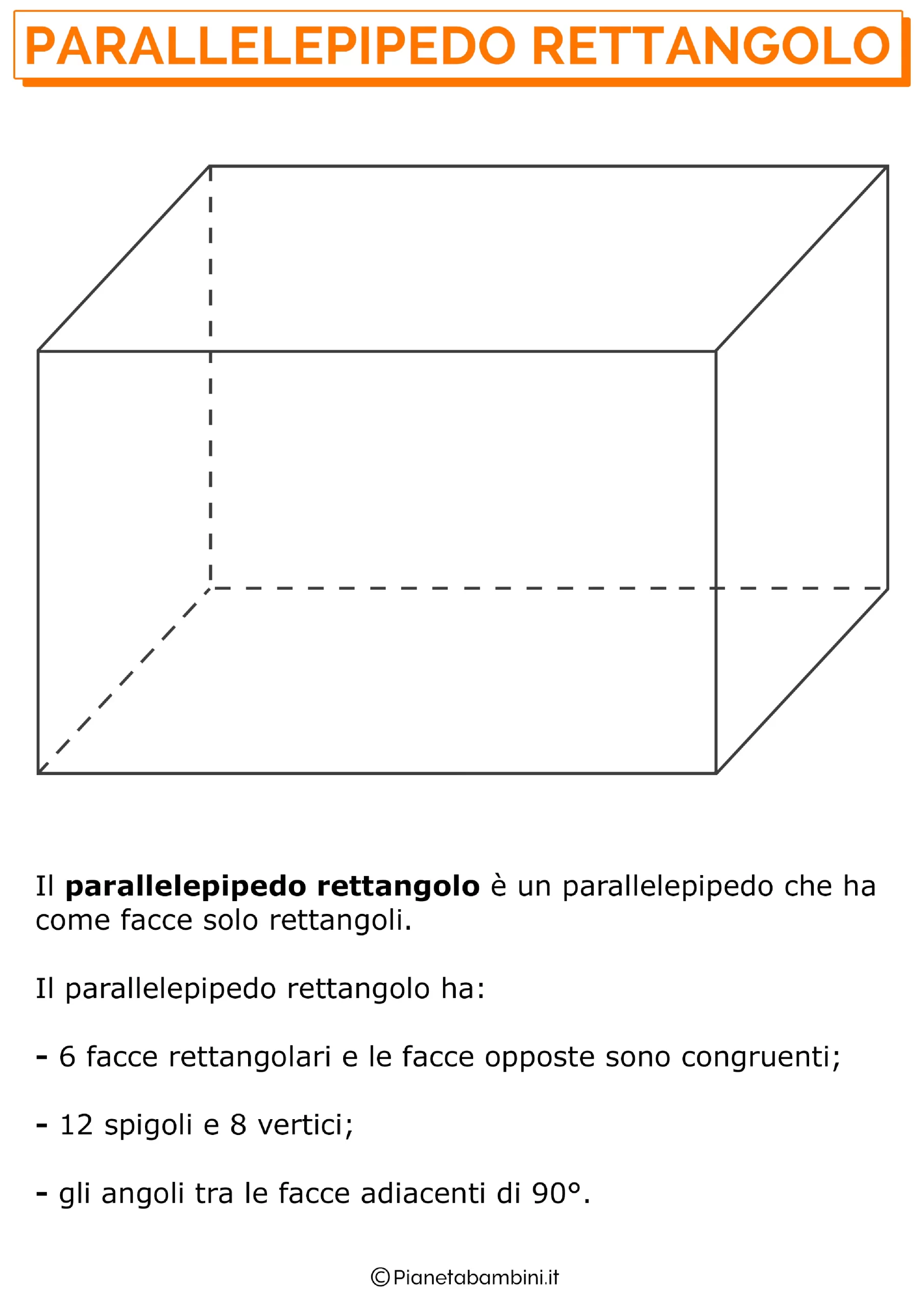
PARALLELEPIPEDO RETTANGOLO
un parallelepipedo rettangolo ha tutte le proprietà del parallelepipedo retto, ma le sue basi sono rettangoli anziché parallelogrammi. Inoltre, il parallelepipedo rettangolo è caratterizzato da proprietà specifiche, come la diagonale principale, che è la linea che unisce i vertici opposti di un rettangolo e ha una lunghezza data dalla radice quadrata della somma dei quadrati delle lunghezze dei lati del rettangolo. Altro concetto importante è quello di volume del parallelepipedo, che si calcola moltiplicando l’area di una base per l’altezza del solido.

In questo formulario, verranno inoltre presentati esempi di calcolo dell’area e del volume del parallelepipedo rettangolo, nonché di altre proprietà, come la superficie laterale e quella totale. In definitiva, lo studio dettagliato della famiglia dei parallelepipedi, in particolare del parallelepipedo rettangolo, rappresenta una conoscenza fondamentale per affrontare problemi e esercizi di geometria in ambito scolastico e universitario.
Il parallelepipedo: definizione e classificazione
Definizione di parallelepipedo
Un parallelepipedo è un poliedro con due basi date da due parallelogrammi congruenti e paralleli, e con quattro facce laterali parallelogrammi.
Equivalentemente, un parallelepipedo può essere definito come un prisma avente due parallelogrammi come basi. È importante sottolineare che un parallelepipedo è sempre un poliedro convesso e può essere classificato in due tipologie: parallelepipedo obliquo e parallelepipedo retto.
Definizione di parallelepipedo obliquo
Un parallelepipedo obliquo è un parallelepipedo in cui gli spigoli della superficie laterale non sono paralleli all’altezza. In altre parole, le facce laterali di un parallelepipedo obliquo sono parallelogrammi, ma non possono essere tutte rettangoli.
Equivalentemente, un parallelepipedo obliquo può essere definito come un prisma obliquo avente due parallelogrammi come basi.
Definizione di parallelepipedo retto
Un parallelepipedo retto è un parallelepipedo avente come facce laterali dei rettangoli, per cui gli spigoli della superficie laterale sono tutti paralleli tra loro, paralleli all’altezza e perpendicolari alle basi.
Equivalentemente, un parallelepipedo retto può essere definito come un prisma retto avente due parallelogrammi come basi.
Il parallelepipedo rettangolo – YouTube
Definizione di parallelepipedo rettangolo
Un parallelepipedo rettangolo è un parallelepipedo retto in cui le basi sono date da due rettangoli.
Equivalentemente, un parallelepipedo rettangolo può essere definito come un prisma retto avente due rettangoli come basi, un esaedro avente come facce dei rettangoli, o un poliedro che ha come facce sei rettangoli.
Classificazione dei parallelepipedi
Per una migliore comprensione, è possibile utilizzare un diagramma di Venn per classificare i parallelepipedi in base alle loro caratteristiche geometriche.
Formule del parallelepipedo rettangolo
Introduzione
Le formule del parallelepipedo sono una particolarizzazione delle formule del prisma. In questo articolo, ci limiteremo a descrivere le formule del parallelepipedo rettangolo, poiché in questo caso le formule sono particolarmente semplici da ricavare.
Volume
Il volume del parallelepipedo rettangolo può essere calcolato utilizzando la formula:
V = abh
oppure utilizzando la formula generale del prisma:
V = S_b · h
dove S_b è l’area della superficie di base del parallelepipedo rettangolo.
Superficie
La superficie totale del parallelepipedo rettangolo è data dalla somma dell’area della superficie laterale e del doppio dell’area della superficie di base:
S_(tot) = 2(ab + ah + bh)
La superficie laterale del parallelepipedo rettangolo può essere calcolata utilizzando la formula:
S_(lat) = 2(ah + bh)
oppure utilizzando la formula generale:
S_(lat) = 2p · h
dove p è il perimetro di base del parallelepipedo rettangolo.
L’area della superficie di base del parallelepipedo rettangolo è data dall’area del rettangolo di base:
S_b = ab
Altezza
L’altezza del parallelepipedo rettangolo può essere calcolata utilizzando la formula:
h = (V)/(S_b)
oppure utilizzando la formula:
h = (S_(lat))/(2p)
Perimetro di base
Il perimetro di base del parallelepipedo rettangolo può essere calcolato utilizzando la formula:
2p = 2a + 2b
oppure utilizzando la formula:
2p = (S_(lat))/(h)
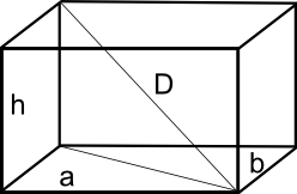
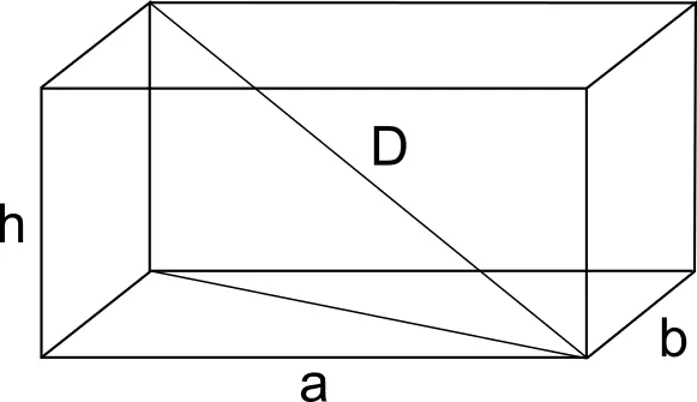
Diagonale
La diagonale del parallelepipedo rettangolo può essere calcolata utilizzando il teorema di Pitagora. Si ha infatti:
D = √(d^2 + h^2) ; D = √(a^2 + b^2 + h^2)
Proprietà del parallelepipedo rettangolo
Introduzione
Il parallelepipedo rettangolo è un solido geometrico molto importante, che presenta diverse proprietà interessanti. In questo articolo, elencheremo le principali proprietà del parallelepipedo rettangolo.
Proprietà principali
Ecco le proprietà principali del parallelepipedo rettangolo:
- Le facce del parallelepipedo rettangolo sono rettangoli.
- Le facce opposte del parallelepipedo rettangolo sono congruenti.
- Le facce del parallelepipedo rettangolo giacciono su piani a due a due paralleli.
- Il parallelepipedo rettangolo ha 6 facce, 8 vertici e 12 spigoli.
- In un parallelepipedo rettangolo ci sono 16 diagonali, di cui 4 diagonali interne e 12 diagonali di superficie.
- Tutti gli angoli diedri interni del parallelepipedo rettangolo hanno un’ampiezza di 90°.
- Il cubo, che è un particolare tipo di parallelepipedo rettangolo, è l’unico solido platonico che rientra nella famiglia dei parallelepipedi e dei prismi.
Conclusioni
Il parallelepipedo rettangolo è un solido geometrico con diverse proprietà interessanti, tra cui le facce rettangolari, le diagonali e gli angoli diedri di ampiezza 90°. Il cubo, invece, è un particolare tipo di parallelepipedo rettangolo, che presenta ulteriori proprietà di simmetria e regolarità.
Fonte: https://www.matematichiamo.it/geometria/parallelepipedo-rettangolo/
Stai guardando: PARALLELEPIPEDO RETTANGOLO