DIVISIONI A DUE CIFRE

La divisione a due cifre è un tipo di divisione eseguita in colonna in cui il divisore è un numero composto da due cifre. La difficoltà dell’algoritmo di calcolo e la mancanza di pratica con le tabelline sono i principali fattori che portano gli studenti a provare disprezzo per questa operazione e, di conseguenza, per la Matematica in generale. Di solito, la matofobia, ovvero la paura della Matematica, si manifesta proprio durante l’apprendimento delle divisioni, quando gli studenti incontrano difficoltà nel comprendere e risolvere i problemi.

Come calcolare le divisioni a due cifre in colonna
Il procedimento per eseguire le divisioni in colonna risulta di per sé complicato per gli alunni, perché richiede diversi passaggi intermedi. Il caso delle divisioni a due cifre in colonna risulta ulteriormente complicato. Nel caso lo riteneste necessario, è consigliabile guidare i bambini in un ripasso ad hoc, per poi dedicarvi con profitto alla spiegazione del caso di divisori a due cifre.
Il metodo per le divisioni a due cifre
Alla scuola primaria il metodo per le divisioni a due cifre viene accompagnato da un esempio-guida. Tuttavia, almeno nelle prime fasi dell’apprendimento, i bambini si pongono delle domande che permettono loro di giungere al completamento dell’operazione. È importante incoraggiarli in tale direzione seguendoli nei vari passaggi e, nel caso vi fossero errori, intervenire prontamente correggendo le imprecisioni sul nascere, senza essere troppo severi ovviamente.
Procedimento
Proponiamoci di calcolare il quoziente e il resto della divisione 2692:69 e procediamo passaggio per passaggio.
Passaggio 1
Si incolonnano il dividendo ed il divisore in colonna, in un’apposita tabella. Dunque, la tabella relativa alla divisione che vogliamo calcolare sarà:
| 2 | 6 | 9 | 2 | ||
| : | 6 | 9 |
Divisioni a due cifre in colonna. – YouTube
Passaggio 2
Si abbassano le cifre del dividendo sufficienti a formare un numero maggiore o al più uguale al divisore. Nell’esempio si abbassano esattamente tre cifre. In questo passo, le domande che i bambini si pongono sono:
- “Posso abbassare solo la prima cifra?” La risposta è no, perché 2 è minore del divisore.
- “Posso abbassare le prime due cifre del dividendo?” Ancora non va bene, perché 26 è minore di 69.
- “Abbasso tre cifre del dividendo?” Il numero ottenuto è 269 ed è maggiore del divisore, dunque va bene.
| 2 | 6 | 9 | 2 |
Divisione a mano: metodo della prova di divisione
La divisione è un’operazione matematica fondamentale che consiste nel trovare quante volte un numero, detto divisore, è contenuto in un altro numero, detto dividendo. Esistono diversi metodi per eseguire la divisione, tra cui il metodo della prova di divisione.
Passo 1: cifre abbassate
Per applicare il metodo della prova di divisione, si inizia con l’abbassare le cifre del dividendo a partire da sinistra, finché non se ne ha abbastanza per formare un numero maggiore o uguale alla cifra delle decine del divisore. Ad esempio, consideriamo la divisione 269 ÷ 6. La cifra delle decine del divisore è 6, quindi il numero da considerare è 26.
Passo 2: candidato quoziente parziale
Si calcola quante volte la decina del dividendo sta nel numero ottenuto nel passo 1, utilizzando la tabellina del divisore. Il risultato sarà il candidato quoziente parziale. Ad esempio, nel nostro caso, la tabellina del 6 ci dice che 6 x 4 = 24, per cui 4 è il candidato quoziente parziale.
Passo 3: moltiplicazione e confronto
Si moltiplica il candidato quoziente parziale per il divisore e si confronta il prodotto ottenuto con le cifre abbassate del dividendo. Si possono verificare due casi:
- Se il prodotto ottenuto è minore o uguale al numero abbassato, allora lo si posiziona sotto quest’ultimo.
- Se il prodotto è maggiore del numero abbassato, allora il candidato quoziente parziale non va bene. In tal caso si considera il precedente del candidato quoziente parziale e si moltiplica per il divisore. Se il prodotto ottenuto è minore delle cifre abbassate, si riporta al di sotto di esse, altrimenti si ripete nuovamente il passaggio.
Nel nostro esempio, il candidato quoziente parziale è 4, che moltiplicato per il divisore dà come risultato 69 x 4 = 276, che è maggiore delle cifre abbassate del dividendo (269). Quindi, il candidato quoziente parziale non va bene e si considera il precedente, ossia 3. Moltiplicando 3 per 69 si ottiene 69 x 3 = 207, che è minore delle cifre abbassate del dividendo (269), quindi lo si posiziona sotto di esse.
Continuando il processo, si ottiene:
| 4 | 3 | |
| 6 | 2 | 0 |
Divisione a due cifre: come eseguirla
Passo 1: Sottrazione in colonna
Per eseguire la divisione a due cifre, è necessario eseguire la sottrazione in colonna tra le cifre abbassate e il prodotto, in modo da ottenere il resto parziale. Ad esempio, se si vuole dividere 2692 per 69, si deve eseguire la sottrazione 269 – 207, che dà per risultato 62.
Passo 2: Divisione del numero ottenuto
Dopo aver ottenuto il resto parziale, si deve abbassare la cifra del dividendo e affiancarla al resto parziale. Successivamente, si deve dividere il numero ottenuto per il divisore, ripetendo i passi 3 e 4 fino alla fine della divisione.
Nell’esempio di cui sopra, il resto parziale è 622 che diviso per 69 restituisce 9. Il 9 viene quindi moltiplicato per il divisore, trascritto sotto il resto parziale e infine sottratto. Si ottiene così un nuovo resto parziale, che può essere utilizzato per il successivo ciclo della divisione.
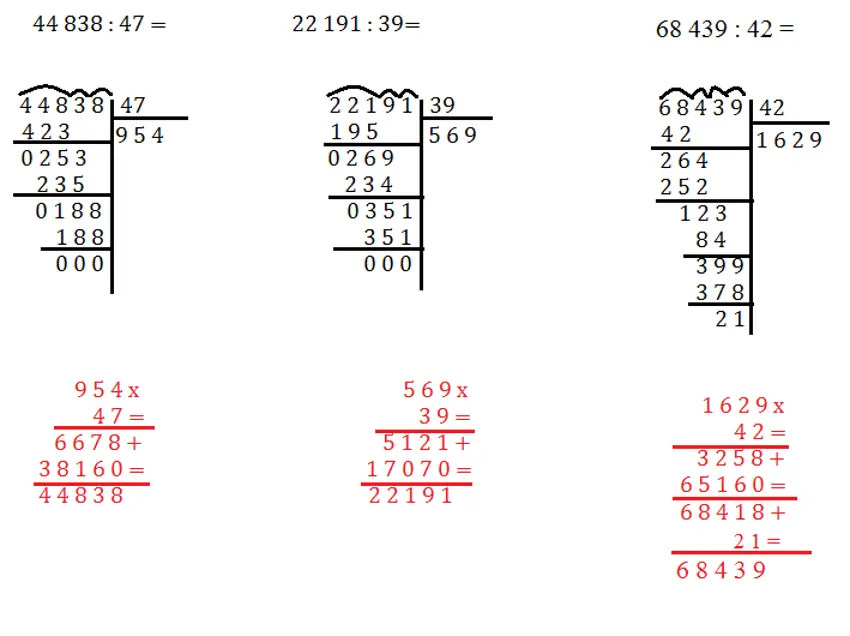
Passo 3: Prova della divisione
Dopo aver svolto la divisione, è possibile eseguire la prova della divisione per verificare se il risultato è corretto. La prova prevede di moltiplicare il quoziente per il divisore e aggiungere l’eventuale resto. Se il risultato finale coincide con il dividendo, allora la divisione è stata eseguita correttamente.
Nell’esempio proposto, il quoziente della divisione è 39 e il resto è 1, quindi il risultato finale è 2692. La prova della divisione prevede quindi di moltiplicare 39 per 69 e aggiungere 1, ottenendo così 2688 + 4 = 2692, che coincide con il dividendo.
Fonte: youmath.it
Stai guardando: DIVISIONI A DUE CIFRE