MEDIA PONDERATA: COS’È, A COSA SERVE E COME SI CALCOLA
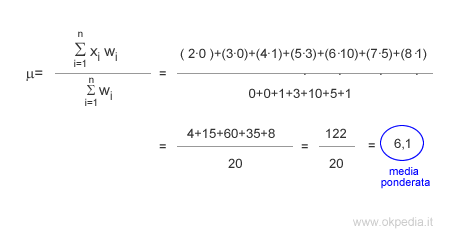
La media ponderata, nota anche come media pesata o media aritmetica ponderata, è utilizzata per calcolare il valore medio di un insieme di numeri tenendo conto dell’importanza di ciascuno di essi, espressa in termini di peso. Pertanto, per determinare la media ponderata, è necessario conoscere sia i numeri che i rispettivi pesi associati. In sintesi, la media ponderata è una variante della media aritmetica che tiene conto dell’influenza del peso di ogni numero sul calcolo del valore medio.
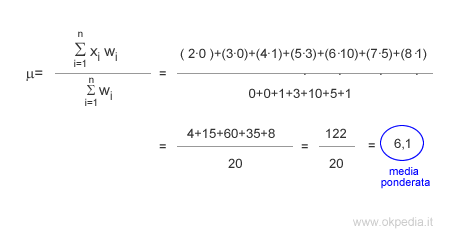
Come calcolare la media ponderata
La media ponderata è una misura statistica utilizzata per calcolare il valore medio di un insieme di dati numerici, tenendo conto del peso di ciascun valore.
Formula della media ponderata
Per calcolare la media ponderata di n valori numerici x_1, x_2, …, x_n e dei rispettivi pesi p_1, p_2, …, p_n, si utilizza la seguente formula:
Media Ponderata = (x_1·p_1+x_2·p_2+…+x_n·p_n)/(p_1+p_2+···+p_n)
In alternativa, si può utilizzare la seguente formula più compatta, che prevede l’utilizzo del simbolo di sommatoria:
Media ponderata = (Σi=1n(x_i·p_i))/(Σi=1np_i)
Significato della media ponderata
La media ponderata è utilizzata per calcolare un valore medio in cui ciascun valore numerico di partenza ha una propria importanza specificata dal relativo peso. Questo significa che i valori con pesi maggiori hanno una maggiore influenza sul valore medio finale.

Media aritmetica, media ponderata, moda – YouTube
Esempi di calcolo della media ponderata
La media ponderata è una misura statistica utile per calcolare il valore medio di un insieme di dati numerici, tenendo conto del peso di ciascun valore. Ecco due esempi pratici di come calcolare la media ponderata:
Esempio 1
Consideriamo i numeri {6, 12, 8, 5, 7} con rispettivi pesi {5, 3, 4, 11, 1}. Per calcolare la media ponderata dobbiamo innanzitutto determinare la somma tra i prodotti di ciascun numero per il corrispondente peso:
6·5+12·3+8·4+5·11+7·1 = 30+36+32+55+7 = 160
La somma dei pesi è invece:
5+3+4+11+1 = 24
Applicando la formula della media ponderata, otteniamo:
Media Ponderata = 160/24 = 6,6
Il risultato è un numero periodico.
Esempio 2
Un altro esempio di utilizzo della media ponderata è il calcolo del voto di laurea. In questo caso, i valori numerici di partenza sono i voti d’esame e i relativi pesi sono i Crediti Formativi Universitari (CFU), che definiscono l’importanza di ciascun esame rispetto al relativo corso di laurea.
Relazione tra media ponderata e media aritmetica
Per comprendere appieno cos’è la media ponderata e qual è la differenza algebrica e statistica rispetto alla media aritmetica (detta semplicemente media), basta ricordarne la definizione e confrontarla con la formula che abbiamo scritto poco sopra.

Media aritmetica
Se consideriamo i seguenti n valori numerici x_1, x_2, …, x_n, la loro media aritmetica è data dalla loro somma divisa per il numero di valori:
Media aritmetica = (x_1+x_2+…+x_n)/(n)
Da qui si capisce che la media aritmetica è una media pesata in cui il peso di ciascun numero è pari a 1.
Media ponderata
La media ponderata, invece, tiene conto del peso di ciascun valore numerico. Supponiamo di avere n valori numerici x_1, x_2, …, x_n e i rispettivi pesi p_1, p_2, …, p_n. La formula della media ponderata è la seguente:
Media Ponderata = (x_1·p_1+x_2·p_2+…+x_n·p_n)/(p_1+p_2+···+p_n)
Relazione tra media ponderata e media aritmetica
Se tutti i pesi dei valori numerici sono uguali a 1, la media ponderata coincide con la media aritmetica. Infatti, sostituendo p_i = 1 per ogni i, si ottiene:
Media ponderata = (x_1+x_2+…+x_n)/(n) = Media aritmetica
Questo significa che la media aritmetica è un caso particolare della media ponderata, in cui tutti i valori hanno lo stesso peso.
Fonte: https://www.matematicamente.it/statistica/media-ponderata/
Stai guardando: MEDIA PONDERATA: COS’È, A COSA SERVE E COME SI CALCOLA