SCOMPOSIZIONI
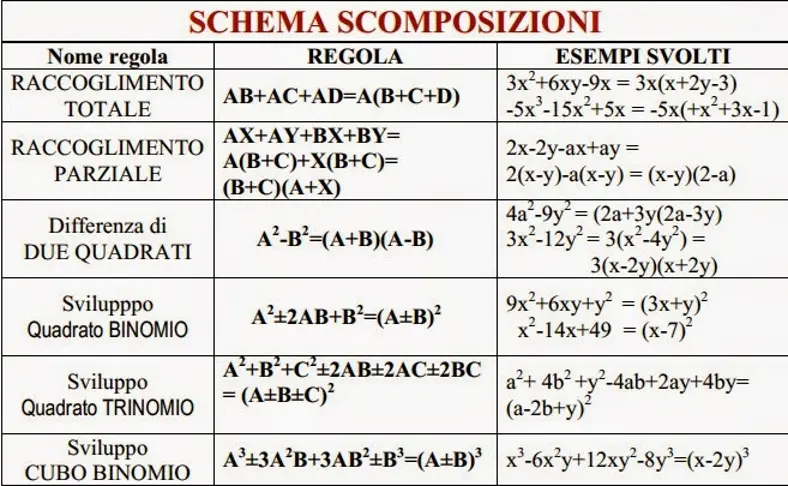
La scomposizione di un polinomio consiste nella scrittura del polinomio come prodotto di polinomi di grado inferiore. Esistono diversi metodi per eseguire la scomposizione, tra cui il raccoglimento, l’applicazione delle regole dei prodotti notevoli o la regola di Ruffini.

Tuttavia, la scelta del metodo da utilizzare dipende dal numero di termini del polinomio e dalla sua forma, e non tutti i polinomi possono essere scomposti. Pertanto, è importante valutare attentamente il polinomio da scomporre prima di procedere con un metodo specifico.
Come scomporre un polinomio
Verifica il fattore comune
Quando si vuole scomporre un polinomio, la prima cosa da fare è verificare se si può effettuare un raccoglimento a fattore comune. Questo significa controllare se c’è un fattore (numerico o letterale) comune a tutti i termini del polinomio. Se si può effettuare il raccoglimento a fattore comune, procedi con il raccoglimento totale.
Tabella di riepilogo per le scomposizioni
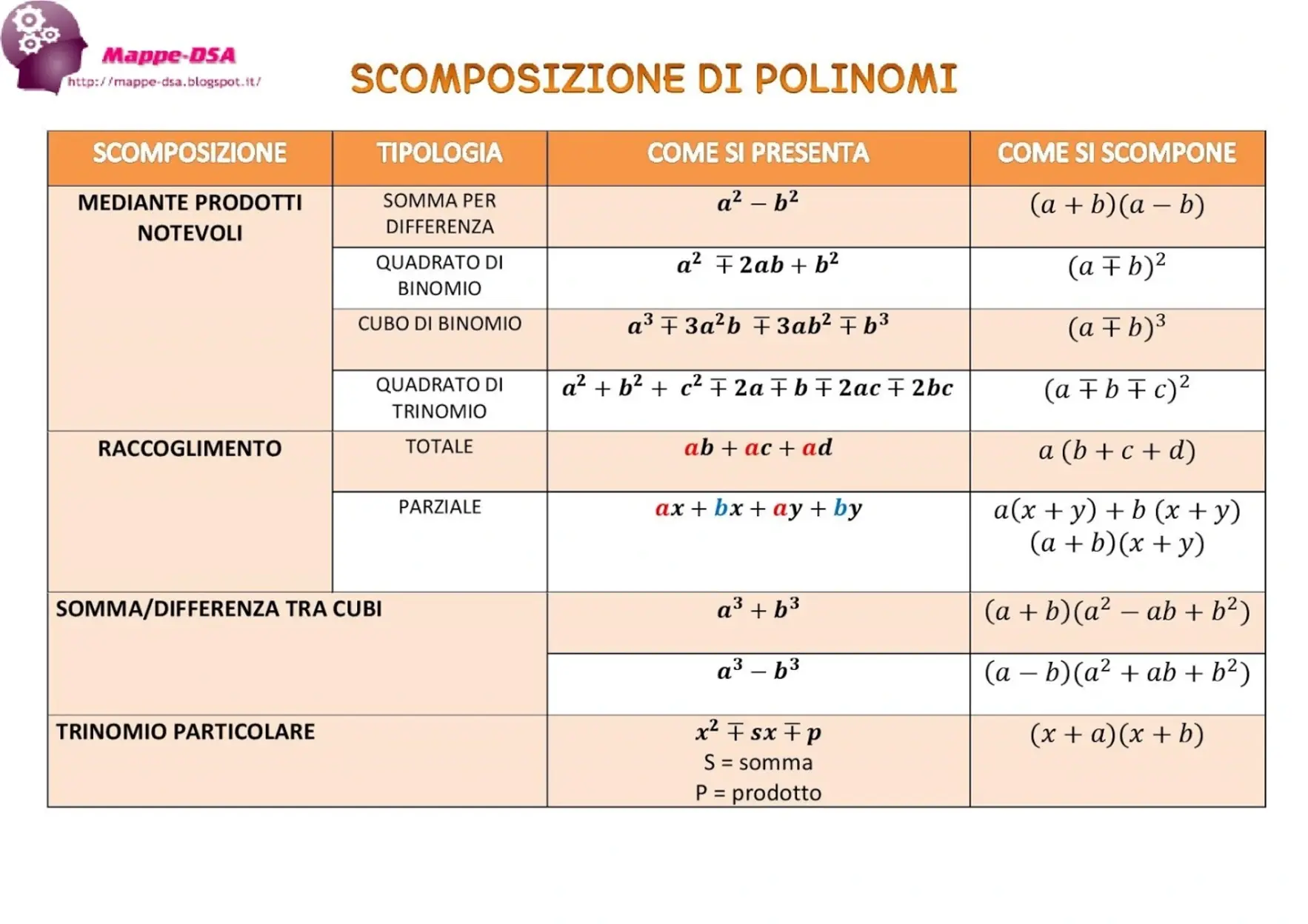
Se il raccoglimento totale non è possibile, utilizza la tabella di riepilogo sulle scomposizioni. Ecco un elenco dei vari tipi di scomposizioni al variare del numero dei termini del polinomio da scomporre:
2 termini
- Differenza di quadrati: a^2-b^2 = (a+b)(a-b)
- Differenza di cubi: a^3-b^3 = (a-b)(a^2+ab+b^2)
- Somma di cubi: a^3+b^3 = (a+b)(a^2-ab+b^2)
- Somma di quadrati: non è scomponibile in R
3 termini
- Quadrato di un binomio: a^2±2ab+b^2 = (a±b)^2
- Trinomio notevole
- Regola di Ruffini
Scomposizione di Polinomi : Introduzione – YouTube
4 termini
- Cubo di binomio: a^3+3a^2b+3ab^2+b^3 = (a+b)^3
- Raccoglimento parziale
- Regola di Ruffini
5 termini
- Regola di Ruffini
6 termini
- Quadrato di un trinomio: a^2+b^2+c^2+2ab+2ac+2bc = (a+b+c)^2
- Raccoglimento parziale
- Regola di Ruffini
7 o più termini
- Raccoglimento parziale (se i termini del polinomio sono in numero pari)
- Regola di Ruffini
Esempi sulla scomposizione di un polinomio
Esempio 1
Consideriamo il polinomio 2x^3+8x^2+8x. Il fattore comune a tutti i termini è 2x, quindi procediamo con un raccoglimento totale:
2x^3+8x^2+8x = 2x(x^2+4x+4)
Il polinomio tra parentesi è lo sviluppo di un quadrato di binomio, quindi la scomposizione completa è:
2x^3+8x^2+8x = 2x(x^2+4x+4) = 2x(x+2)^2
Esempio 2
Prendiamo in considerazione il polinomio 2ab+3a+10b+15. Non essendoci fattori comuni a tutti i termini, non possiamo effettuare un raccoglimento totale. Poiché il polinomio ha quattro termini, possiamo provare a scomporlo con un raccoglimento parziale:
Raccogliamo il fattore a nei primi due termini e il fattore 5 negli ultimi due:
2ab+3a+10b+15 = a(2b+3)+5(2b+3)
Osservando che abbiamo ottenuto una coppia di parentesi tonde con gli stessi elementi, possiamo completare il raccoglimento e la scomposizione:
2ab+3a+10b+15 = a(2b+3)+5(2b+3) = (2b+3)(a+5)

Esempio 3
Consideriamo il polinomio 3a^3-24. Possiamo effettuare un raccoglimento totale del fattore 3:
3a^3-24 = 3(a^3-8)
Il polinomio tra parentesi è una differenza di cubi, quindi la scomposizione completa è:
3a^3-24 = 3(a^3-8) = 3(a-2)(a^2+2a+4)
Fonte: Skuola.net
Stai guardando: SCOMPOSIZIONI