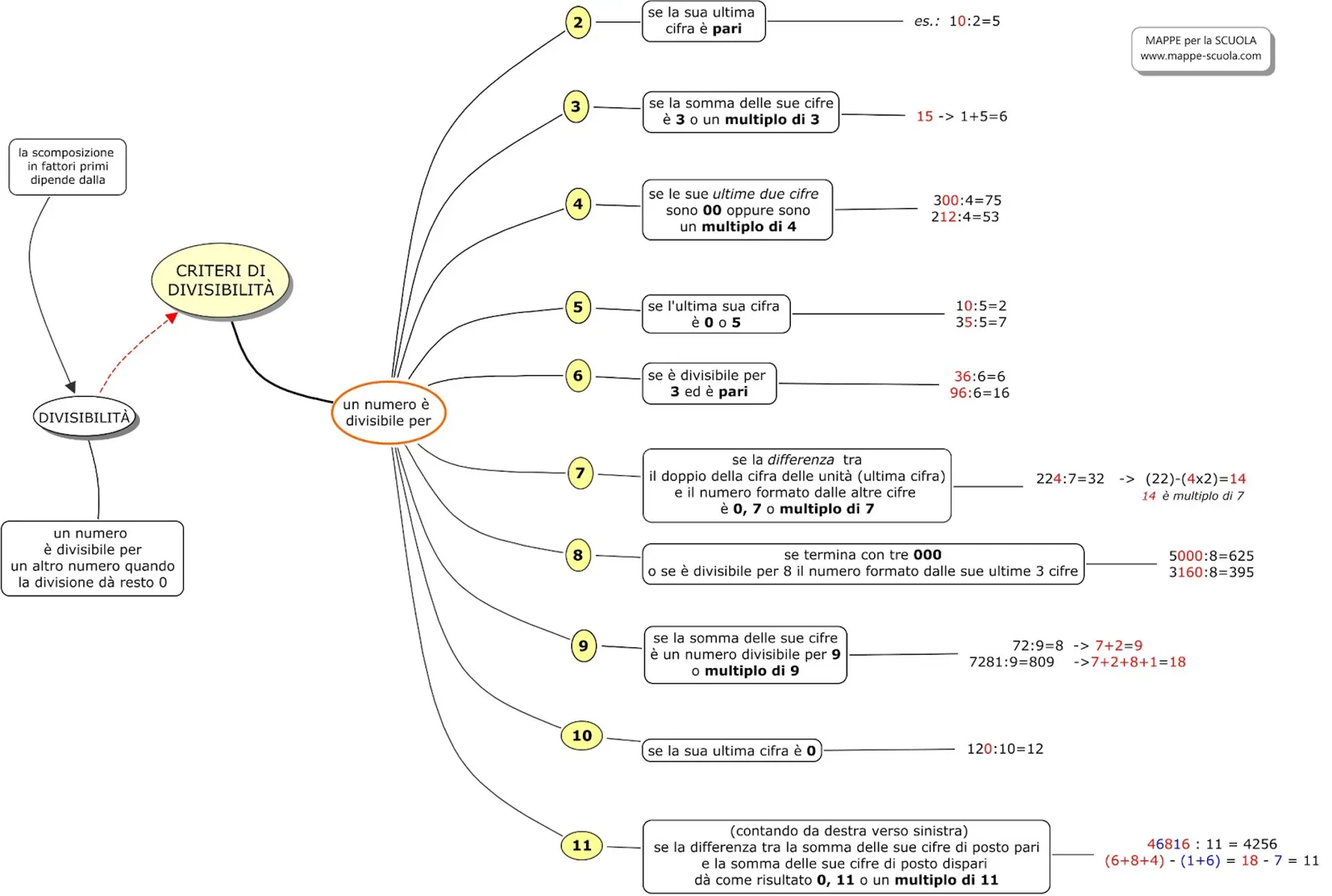
CRITERI DI DIVISIBILITÀ

I criteri di divisibilità sono regole che consentono di determinare in anticipo se un numero è divisibile per un altro numero specifico senza eseguire la divisione. Questi criteri sono applicabili ai numeri naturali più comuni, come ad esempio 2, 3, 5, 7 e 11. In questa lezione approfondiremo tutti i possibili criteri di divisibilità, ma è importante sottolineare che non è necessario conoscerli tutti a memoria. È sufficiente ricordare quelli più famosi o quelli che vengono utilizzati con maggiore frequenza.

Criteri di Divisibilità
Criterio di Divisibilità per 2
Il criterio di divisibilità per 2 stabilisce che un numero è divisibile per 2 se è pari, ovvero se la sua cifra delle unità è 0, 2, 4, 6 o 8.
Ad esempio, 72, 140, 1876, 7865432036 sono tutti divisibili per 2.
Criterio di Divisibilità per 3
Il criterio di divisibilità per 3 afferma che un numero è divisibile per 3 se la somma delle sue cifre è un multiplo di 3.
Ad esempio, il numero 147 è divisibile per 3 in quanto 1+4+7=12, che è un multiplo di 3. Anche 36513 è divisibile per 3, poiché 3+6+5+1+3=18, che è anch’esso un multiplo di 3.
Criterio di Divisibilità per 5
Il criterio di divisibilità per 5 stabilisce che un numero è divisibile per 5 se la sua cifra delle unità è 0 oppure 5.
Ad esempio, 890, 1445 e 14975 sono tre numeri divisibili per 5.
Criteri di divisibilità – YouTube
Criterio di Divisibilità per 7
Il criterio di divisibilità per 7 afferma che un numero è divisibile per 7 se il valore assoluto della differenza fra il numero scritto senza la cifra delle unità e il doppio della cifra delle unità è uguale a 0, 7, o un suo multiplo.
Ad esempio, il numero 91 è divisibile per 7, in quanto il numero privato della cifra delle unità è 9, il doppio della cifra delle unità è 2 e 9-2=7. Allo stesso modo, 119 è divisibile per 7, poiché 11 (numero senza cifra unità) meno 18 (doppio cifra unità) è uguale a -7 (il cui valore assoluto è proprio 7).
Criteri di Divisibilità
Criterio di Divisibilità per 11
Il criterio di divisibilità per 11 stabilisce che un numero è divisibile per 11 se la differenza (in valore assoluto) tra la somma delle cifre di posto dispari e la somma delle cifre di posto pari è uguale a 0, 11, o un suo multiplo.
Ad esempio, il numero 297 è divisibile per 11 in quanto |(2+7)-9|=0, dove 2+7 rappresenta la somma delle cifre di posto dispari (2 e 7 sono le cifre di posto uno e tre), mentre 9 è la cifra di posto pari. Inoltre, il numero 2453 è divisibile per 11 poiché |(2+5)-(4+3)| = 0.
Caso particolare del criterio di divisibilità per 11: se un numero ha un numero pari di cifre e se le cifre vicine sono a due a due uguali, allora è divisibile per 11. Ad esempio, 55, 88, 1122, 889955, 77881144 sono tutti divisibili per 11.
Criterio di Divisibilità per 4
Il criterio di divisibilità per 4 stabilisce che un numero è divisibile per 4 se le sue ultime due cifre soddisfano le seguenti condizioni:
- La cifra delle decine è dispari e quella delle unità è 2 o 6
- La cifra delle decine è pari e quella delle unità è 0, 4 o 8.
Ad esempio, 136, 752, 14180, 82168 e 12652 sono tutti divisibili per 4.
Criterio di Divisibilità per 6
Il criterio di divisibilità per 6 stabilisce che un numero è divisibile per 6 se è divisibile sia per 2 che per 3.
Ad esempio, il numero 72 è divisibile per 6 in quanto è divisibile sia per 2 (essendo pari) che per 3 (7+2=9, che è multiplo di 3). Allo stesso modo, 378 e 2046 sono divisibili per 6.
Criteri di Divisibilità per alcuni numeri primi
Criterio di Divisibilità per 9
Un numero è divisibile per 9 se la somma delle sue cifre è 9 o un suo multiplo. Ad esempio, 54, 279 e 6876 sono divisibili per 9.
Criterio di Divisibilità per 10
Un numero è divisibile per 10 se la sua cifra delle unità è pari a zero.
Criterio di Divisibilità per 13
Un numero è divisibile per 13 se la somma tra il numero senza la cifra delle unità e quattro volte la cifra delle unità è 0, 13 oppure un suo multiplo. Ad esempio, 221 è divisibile per 13 poiché 22+4×1=26 che è un multiplo di 13. Allo stesso modo, 377 è divisibile per 13 poiché 37+4×7=65 che è un multiplo di 13. In caso il numero ottenuto dalla somma sia grande e non sia possibile verificare immediatamente se è o meno un multiplo di 13, si può applicare nuovamente lo stesso criterio ad esso.
Criterio di Divisibilità per 17
Un numero è divisibile per 17 se il valore assoluto della differenza tra il numero scritto senza la cifra delle unità e il quintuplo della cifra delle unità è uguale a 0, 17 o un suo multiplo. Ad esempio, 391 è divisibile per 17 poiché 39-5×1=34 che è un multiplo di 17.
Criterio di Divisibilità per 23
Un numero è divisibile per 23 se la somma tra il numero scritto senza la cifra delle unità e 7 volte la cifra delle unità è uguale a 0, 23 o un suo multiplo. Ad esempio, 598 e 1794 sono divisibili per 23.
Criterio di Divisibilità per 10^n
Un numero è divisibile per 10^n, con n ∈ N, n ≥ 1 se esso termina con n zeri.
Criterio di Divisibilità per numeri della forma n = pq
Un numero è divisibile per n = pq, dove p e q sono numeri primi, se esso è divisibile sia per p che per q. Ad esempio, un numero è divisibile per 26 = 2×13 se è divisibile sia per 2 che per 13.
Fonte: Wikipedia
Stai guardando: CRITERI DI DIVISIBILITÀ