TABELLA DEGLI SVILUPPI DI TAYLOR-MC LAURIN

La tabella degli sviluppi di Taylor-McLaurin, anche nota come tabella degli sviluppi fondamentali, è una lista di sviluppi in serie di Taylor per le funzioni elementari con centro in x0=0. Questa tabella è utile sia in ambito teorico che pratico, poiché fornisce in modo preciso gli sviluppi di queste funzioni e li considera come noti. Grazie a questa tabella, è possibile evitare di dover calcolare manualmente gli sviluppi di Taylor per le funzioni elementari ogni volta che se ne ha bisogno.

Sviluppi di Taylor-Mc Laurin di funzioni elementari
Con sviluppo di Taylor-McLaurin si intende uno sviluppo di Taylor con centro x0=0.
Sviluppo di Taylor-Mc Laurin della funzione esponenziale
L’espressione del sviluppo di Taylor-Mc Laurin della funzione esponenziale è:
ex = Σn=0∞(xn)/(n!) ∀ x∈ R
In forma estesa, si ha:
ex = 1 + x + (x2)/(2) + (x3)/(6) + (x4)/(24) + (x5)/(120) + ··· + (xn)/(n!) + o(xn) ∀ x∈R
Sviluppo di Taylor-Mc Laurin della funzione logaritmica
L’espressione del sviluppo di Taylor-Mc Laurin della funzione logaritmica è:
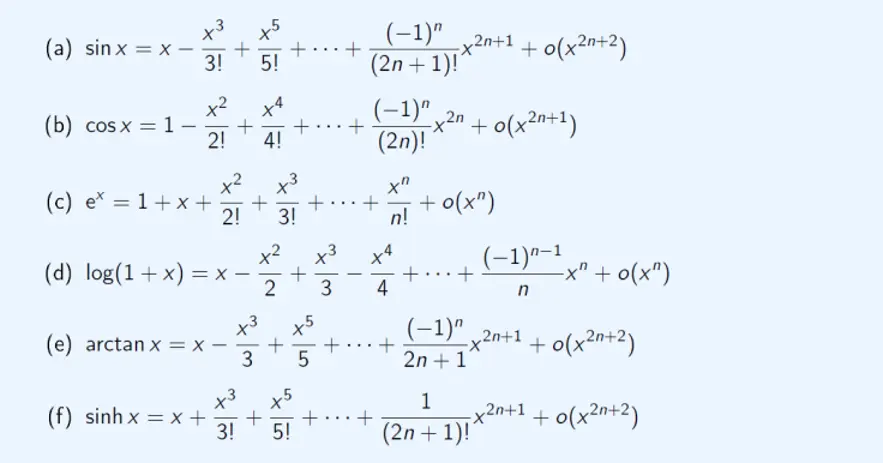
ln(1+x) = Σn=1+∞ (-1)n+1 (xn)/(n) per |x| < 1
In forma estesa, si ha:
ln(1+x) = x – (x2)/(2) + (x3)/(3) – (x4)/(4) + (x5)/(5) + ··· + ((-1)n+1)/(n) xn + o(xn) per |x| < 1
Sviluppi di Taylor McLaurin – YouTube
Sviluppo di Taylor-Mc Laurin del binomio
L’espressione del sviluppo di Taylor-Mc Laurin del binomio è:
(1+x)α = Σn=0∞ α choose n xn per |x| < 1
dove con:
α choose n = (α(α-1)(α-2)··· (α-n+1))/(n!)
Non si intende il coefficiente binomiale standard, bensì il coefficiente binomiale generalizzato.
Sviluppo di Taylor-McLaurin delle funzioni trigonometriche e inverse
Sviluppo di Taylor-McLaurin della tangente
L’espansione di Taylor della funzione tangente (tan) in corrispondenza dello zero è:
tan(x) = x + x3⁄3 + 2⁄15x5 + O(x6)
per |x| < π⁄2.
Sviluppo di Taylor-McLaurin della secante
L’espansione di Taylor della funzione secante (sec) in corrispondenza dello zero è:
sec(x) = 1 + x2⁄2 + 5⁄24x4 + 61⁄720x6 + 277⁄8064x8 + 50521⁄3628800x10 + O(x10)
per |x| < π⁄2.
Sviluppo di Taylor-McLaurin dell’arcoseno
L’espansione di Taylor della funzione arcoseno (arcsin) in corrispondenza dello zero è:
arcsin(x) = x + x3⁄6 + 3⁄40x5 + 5⁄112x7 + 35⁄1152x9 + O(x9)
per |x| < 1.
Sviluppo di Taylor-McLaurin dell’arcocoseno
L’espansione di Taylor della funzione arcocoseno (arccos) in corrispondenza dello zero è:
arccos(x) = π⁄2 – x – x3⁄6 – 3⁄40x5 – 5⁄112x7 – 35⁄1152x9 + O
Sviluppo di Taylor-Mc Laurin dell’arcotangente
L’arcotangente è la funzione inversa della tangente, definita per valori di x compresi tra -π/2 e π/2.
Il suo sviluppo di Taylor-McLaurin troncato al nono termine è il seguente:
arctan(x) = x – (x^3)/3 + (x^5)/5 – (x^7)/7 + (x^9)/9 + o(x^9) per |x| < 1
Il simbolo o(x^9) indica il resto del termine in ordine superiore e indica che il termine successivo è dell’ordine di x^9.
Sviluppo di Taylor-Mc Laurin delle funzioni iperboliche
Le funzioni iperboliche sono definite come:
- sinh(x) = (e^x – e^-x)/2
- cosh(x) = (e^x + e^-x)/2
- tanh(x) = sinh(x)/cosh(x)
- arsinh(x) = ln(x + sqrt(x^2 + 1))
- arcosh(x) = ln(x + sqrt(x^2 – 1))
- artanh(x) = 0.5 ln((1 + x)/(1 – x))
Loro sviluppo di Taylor-McLaurin troncato al nono termine sono i seguenti:
Sviluppo di Taylor-Mc Laurin del seno iperbolico
sinh(x) = x + (x^3)/6 + (x^5)/120 + (x^7)/5040 + (x^9)/362880 + o(x^9)
Sviluppo di Taylor-Mc Laurin del coseno iperbolico
cosh(x) = 1 + (x^2)/2 + (x^4)/24 + (x^6)/720 + (x^8)/40320 + o(x^9)
Sviluppo di Taylor-Mc Laurin dell’arcotangente iperbolica
arctanh(x) = x + (x^3)/3 + (x^5)/5 + (x^7)/7 + (x^9)/9 + o(x^9)
Sviluppo di Taylor-Mc Laurin dell’arcoseno iperbolico
arcsinh(x) = x – (x^3)/6 + (3)/40(x^5) – (5)/112(x^7) + (35)/1152(x^9) + o(x^9)
Le funzioni iperboliche hanno numerose applicazioni in matematica e in fisica, in particolare nella descrizione del moto armonico semplice e di altri fenomeni ondulatori.
Fonte: Wikipedia
Stai guardando: TABELLA DEGLI SVILUPPI DI TAYLOR-MC LAURIN