INTEGRALI PER PARTI
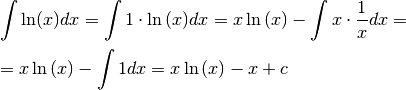
Il teorema di integrazione per parti è un risultato utile della teoria degli integrali secondo Riemann, che consente di calcolare integrali definiti e indefiniti quando l’integranda è un prodotto di funzioni, di cui una è facile da integrare come derivata. La regola che discende da questo teorema consente di calcolare agevolmente tali integrali. Tuttavia, l’utilizzo della regola richiede la comprensione delle proprietà delle funzioni coinvolte nel prodotto e della loro derivata. In tal modo, si può determinare se la regola è opportuna per risolvere il problema.
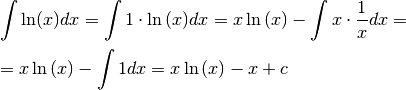
Formula di integrazione per parti
Integrazione per parti per integrali definiti
La formula di integrazione per parti è una tecnica utile per risolvere integrali di prodotti di funzioni. Esistono due varianti della tecnica: una per gli integrali definiti e una per gli integrali indefiniti.
Nel caso degli integrali definiti, supponiamo che f(x) e g(x) siano due funzioni continue e che le loro derivate siano pure continue su un intervallo [a,b]. Allora, la formula di integrazione per parti è la seguente:
∫ab f(x)g'(x)dx = f(b)g(b)-f(a)g(a)-∫ab f'(x)g(x)dx
Integrazione per parti per integrali indefiniti
Nel caso degli integrali indefiniti, la formula di integrazione per parti è la seguente:
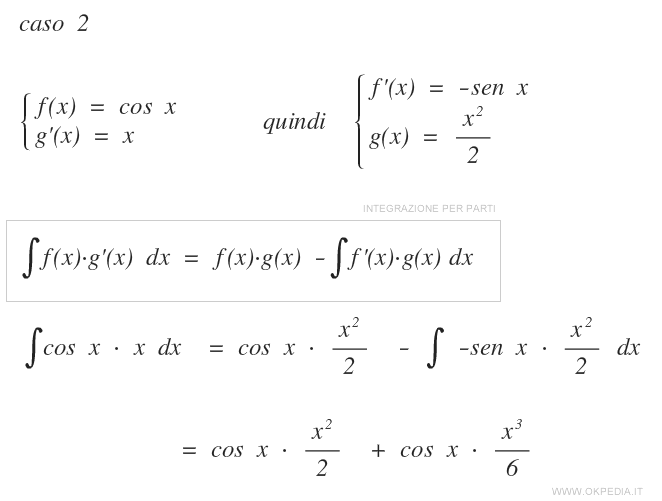
∫f(x)g'(x)dx = f(x)g(x)-∫f'(x)g(x)dx+c
dove c è una costante arbitraria.
Fonte: Wikipedia.
Integrazione per Parti – YouTube
Il Significato della Formula di Integrazione per Parti
Come Funziona la Formula di Integrazione per Parti
La formula di integrazione per parti è un metodo di calcolo che ci consente di risolvere integrali di prodotti di funzioni. In particolare, se dobbiamo calcolare l’integrale di un prodotto di due funzioni f e g’, dove g’ è la derivata di una terza funzione g, possiamo passare a calcolare un nuovo integrale sostituendo g’ con la sua primitiva g e f con la sua derivata f’. La formula di integrazione per parti nel caso indefinito è la seguente:
∫f(x)g'(x)dx = f(x)g(x)-∫f'(x)g(x)dx+c
dove c è una costante arbitraria.
Come Applicare la Formula di Integrazione per Parti
Per applicare la formula di integrazione per parti, è importante seguire questi due passaggi:
- Trovare la primitiva della derivata g’;
- Passare a un integrale più semplice da calcolare rispetto a quello di partenza.
Esempio di Applicazione della Formula di Integrazione per Parti
Consideriamo l’integrale ∫01 x e^x dx. Inizialmente, potrebbe sembrare difficile da risolvere, ma utilizzando la formula di integrazione per parti, possiamo calcolarlo facilmente. Prendiamo g'(x) = e^(x), da cui g(x) = e^(x), e f(x) = x, da cui f'(x) = 1. Quindi, il prodotto che si ottiene nel nuovo integrale è f'(x)g(x) = e^(x). Applicando la formula di integrazione per parti, otteniamo:
∫01 x e^x dx = [xe^x] 01 – ∫01 1 · e^x dx = e – [e^1 – e^0] = 1
Come Usare la Formula di Integrazione per Parti
Procedimento Generale per Calcolare gli Integrali per Parti

La formula di integrazione per parti è un metodo utile per risolvere integrali di prodotti di funzioni. Per utilizzare questa formula, è importante seguire i seguenti passaggi:
- Riconoscere le due funzioni che costituiscono l’integranda come un prodotto di due funzioni.
- Individuare, tra le due funzioni, la derivata g'(x) e la primitiva f(x). Per individuare la derivata g'(x), è importante scegliere una primitiva g(x) facile da calcolare. Invece, per individuare la primitiva f(x), è importante scegliere una derivata f'(x) che semplifichi il nuovo integrale.
- Applicare la formula di integrazione per parti.
Esempio di Applicazione della Formula di Integrazione per Parti
Consideriamo l’integrale ∫01 x e^x dx. Per utilizzare la formula di integrazione per parti, identifichiamo le due funzioni f e g’ come x e e^x, rispettivamente. La derivata g'(x) è e^x, quindi scegliamo g(x) = e^x come primitiva. La primitiva di f(x) = x è (1/2) x^2, quindi scegliamo f'(x) = 1. Il prodotto g(x) f'(x) è e^x. Applicando la formula di integrazione per parti, otteniamo:
∫01 x e^x dx = [xe^x] 01 – ∫01 1 · e^x dx = e – [e^1 – e^0] = 1
Quando Utilizzare la Formula di Integrazione per Parti
La formula di integrazione per parti è particolarmente utile quando si hanno prodotti di funzioni complesse che non possono essere facilmente integrate utilizzando altre tecniche. Inoltre, può essere utilizzata anche per risolvere integrali definiti. Tuttavia, è importante notare che questa formula non è sempre la soluzione migliore e ci sono casi in cui altre tecniche possono essere più appropriate.
Come Capire se e Quando Integrare per Parti
Non esiste un metodo sicuro per risolvere tutti gli integrali utilizzando la formula di integrazione per parti, poiché ci possono essere diverse tecniche che possono essere applicate. Tuttavia, ci sono alcune situazioni in cui la formula di integrazione per parti potrebbe essere utile:
Prodotto di Due Funzioni
Se l’integranda è il prodotto di due funzioni, è probabile che la formula di integrazione per parti possa essere utile.
Una delle Due Funzioni è la Derivata di una Primitiva Immediata
Se l’integranda è il prodotto di due funzioni, e una di queste è la derivata di una primitiva immediata, come funzioni esponenziali, trigonometriche, potenze di x, e così via, può essere utile utilizzare la formula di integrazione per parti.
Semplificazione del Nuovo Integrale
Se l’integranda è il prodotto di due funzioni e derivando una delle due funzioni si ottiene un nuovo integrale semplice moltiplicando la derivata per la primitiva dell’altra funzione, allora può essere utile utilizzare la formula di integrazione per parti.
Casi Particolari
Esistono alcuni casi particolari in cui la formula di integrazione per parti può essere utile. Ad esempio, se l’integranda è del tipo f(x)g(x^n), può essere utile scegliere u = x^n come sostituzione per semplificare l’integrale.
Esempi di Applicazione della Formula per Parti
La comprensione della logica alla base della formula di integrazione per parti è essenziale per risolvere gli esercizi. Ecco alcuni esempi:
Esempio 1
Supponiamo di dover calcolare l’integrale
∫x^2ln(x)dx
In questo caso, possiamo utilizzare la formula di integrazione per parti. Individuiamo la derivata g'(x) e la primitiva f(x) come segue:
g'(x) = x^2 → g(x) = (x^3)/(3)
f(x) = ln(x) → f'(x) = (1)/(x)
Calcoliamo il prodotto g(x)f'(x) a parte:
f'(x)g(x) = (x^3)/(3)·(1)/(x) = (x^2)/(3)
Applicando la formula di integrazione per parti, otteniamo:
∫x^2ln(x)dx = (x^3)/(3)ln(x)-∫(x^3)/(3)·(1)/(x)dx+c = (x^3)/(3)ln(x)-∫(x^2)/(3)dx+c
Esempio 2
Per altri esempi e la pratica degli esercizi, è possibile consultare la sezione dedicata di esercizi svolti sulla formula di integrazione per parti.
Fonte: Math.it.
Integrare per parti due o più volte
Certi integrali richiedono l’applicazione della formula per parti più di una volta. Questo è tipico nel caso in cui abbiamo funzioni con derivate cicliche come l’esponenziale y = e^(x) o funzioni come seno e coseno. Inoltre, è possibile che la funzione da derivare si semplifichi in più passi di derivazione, come nel caso delle potenze di x, che perdono un grado ad ogni iterazione.
Consideriamo ad esempio l’integrale ∫x^3cos(x)dx. Scegliamo g'(x) = cos(x) e f(x) = x^3 e applichiamo la formula di integrazione per parti. Calcoliamo la derivata f'(x) e una primitiva g(x) a parte. Quindi otteniamo:
∫x^3cos(x)dx = x^3sin(x)-∫3x^2sin(x)dx
Limitiamoci a considerare il nuovo integrale e applichiamo di nuovo la formula, considerando g'(x) = sin(x) e f(x) = x^2:
3∫x^2sin(x)dx = 3[x^2(-cos(x))-∫2x(-cos(x))dx] = -3x^2cos(x)+6∫xcos(x)dx
Rimane da calcolare 6∫xcos(x)dx e il completamento dell’esempio viene lasciato alla soluzione individuale.
Nota bene: attenzione a non perdere per strada coefficienti e segni quando si reitera l’applicazione della formula per parti.
Integrali per parti particolarissimi
In questo articolo affrontiamo due tipi di integrali molto particolari che possono essere risolti per parti: i finti prodotti e gli integrali che conducono ad equazioni.
Finti prodotti
Spesso ci troviamo a dover calcolare le primitive di funzioni elementari come il logaritmo naturale e l’arcotangente che non possono essere integrate con nessuno dei metodi conosciuti.
Tuttavia, anche in questi casi possiamo utilizzare il metodo per parti. In particolare, possiamo considerare come secondo fattore:
g'(x) = 1
e integrare per parti prendendo proprio come derivata g'(x) = 1. In questo modo possiamo ottenere un finto prodotto e applicare il metodo per parti. Ad esempio:
∫ ln(x)dx = ∫ 1·ln(x)dx
Scegliamo come derivata e primitiva:
g'(x) = 1 ; f(x) = ln(x)
da cui le corrispondenti primitiva e derivata:
g(x) = x ; f'(x) = (1)/(x)
e in definitiva:
∫ln(x)dx = ∫1·ln(x)dx = xln(x)-∫x·(1)/(x)dx = xln(x)-∫1dx = xln(x)-x+c
Integrali che conducono ad equazioni
In alcuni casi, l’integrale può condurre ad un’equazione che deve essere risolta per ottenere la soluzione finale. Ad esempio:
∫cos(x)dx = sin(x) + C
In questo caso, risolviamo l’equazione ∫cos(x)dx = sin(x) + C ottenendo la soluzione ∫cos(x)dx = sin(x) + C.
In conclusione, questi due tipi di integrali particolari possono essere risolti utilizzando il metodo per parti e, se necessario, risolvendo eventuali equazioni che conducono alla soluzione finale.
Fonte: https://www.matematika.it/integrali-per-parti/
Integrali per parti che conducono ad equazioni
In alcuni casi, l’integrazione per parti non porta direttamente al calcolo dell’integrale. Tuttavia, se l’integranda è costituita dal prodotto di due funzioni con derivate cicliche, possiamo utilizzare una doppia integrazione per giungere ad un integrale che coincide con quello di partenza. A questo punto, possiamo trattare l’uguaglianza come un’equazione.
Ad esempio, consideriamo l’integrale:
∫e^xsin(x)dx = e^(x)sin(x)-∫e^xcos(x)dx = e^(x)sin(x)-[e^(x)cos(x)-∫e^x(-sin(x))dx] = e^(x)sin(x)-e^(x)cos(x)-∫e^xsin(x)dx
Riscriviamo l’uguaglianza costituita dal primo e dall’ultimo termine della catena come un’equazione nell’incognita:
I = ∫e^xsin(x)dx
e otteniamo l’equazione:
I = e^(x)sin(x)-e^(x)cos(x)-I
da cui ricaviamo:
2I = e^(x)sin(x)-e^(x)cos(x) ; I = (1)/(2)e^(x)(sin(x)-cos(x))
Tuttavia, dobbiamo ricordarci della costante additiva e quindi la soluzione finale sarà:
∫e^xsin(x)dx = (1)/(2)e^(x)(sin(x)-cos(x))+c
Stai guardando: INTEGRALI PER PARTI