ANGOLO CONCAVO E CONVESSO
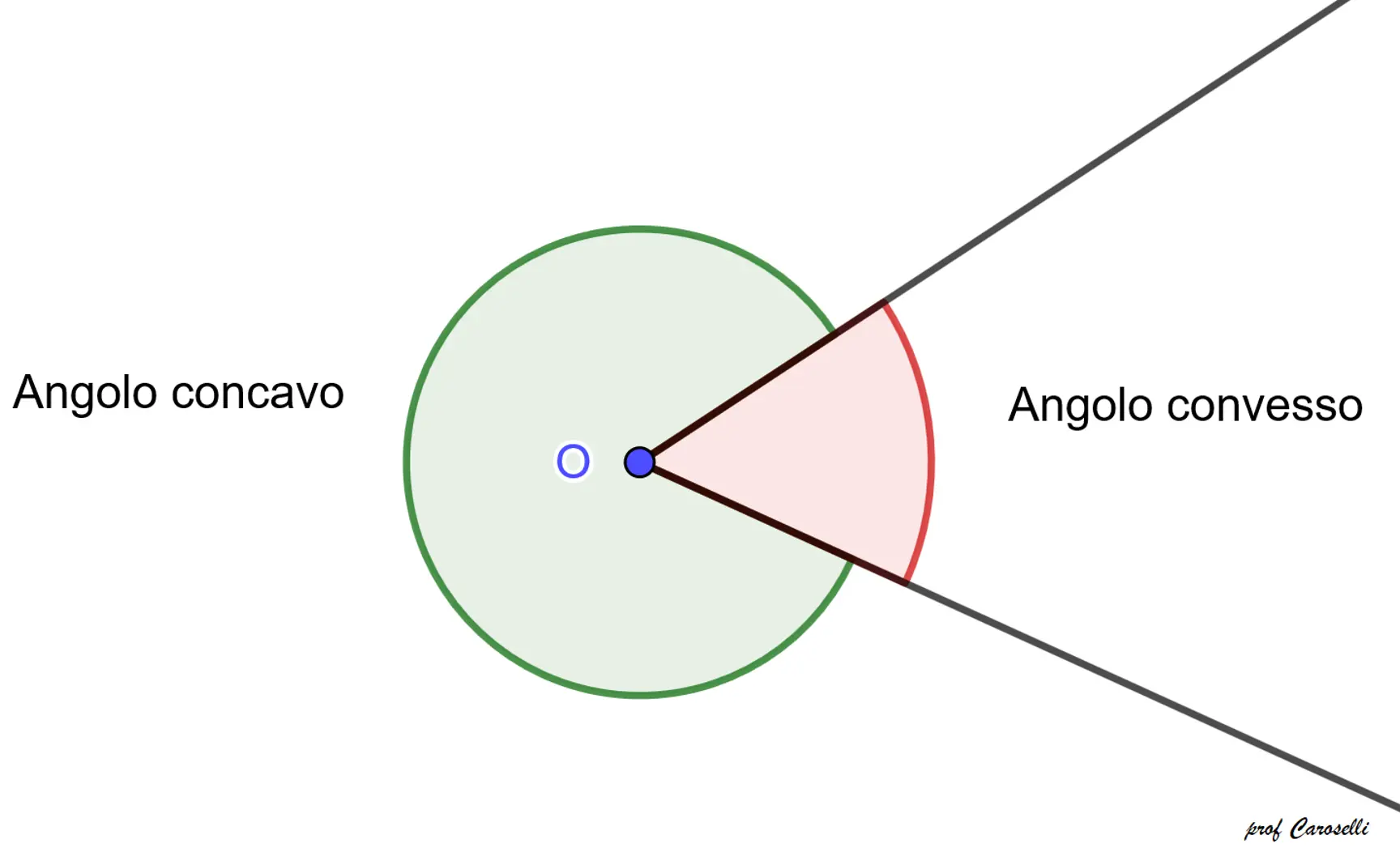
La distinzione tra angoli concavi e convessi si basa sull’estensione dei loro lati e sulla misura dell’ampiezza dell’angolo. Un angolo concavo è caratterizzato dal fatto che i prolungamenti dei suoi lati si trovano all’interno dell’angolo stesso, mentre un angolo convesso è tale se i prolungamenti dei suoi lati si trovano all’esterno dell’angolo. Dopo aver discusso dei metodi per il confronto tra angoli, è importante considerare le proprietà distintive degli angoli concavi e convessi. Questa guida si concentrerà sulla caratterizzazione di entrambi i tipi di angoli.

Introduzione agli angoli concavi e convessi: i prolungamenti
In geometria, per comprendere la classificazione degli angoli concavi e convessi, è necessario prima spiegare ai bambini cosa sono i prolungamenti di segmenti e semirette.
Prolungamenti di un segmento
Per costruire i prolungamenti di un segmento di estremi A e B, si dispone il righello in modo che tocchi i due estremi A e B, e si tracciano due linee tratteggiate che proseguono nella stessa direzione del segmento, una dall’estremo A e l’altra dall’estremo B. Esse saranno i prolungamenti del segmento AB.
Prolungamento di una semiretta
Per costruire il prolungamento di una semiretta, si allinea il righello alla semiretta e si traccia una linea tratteggiata dalla parte opposta alla semiretta, partendo dalla sua origine.
Formalmente, i prolungamenti di un segmento sono le semirette aventi origine negli estremi del segmento e direzione data dalla retta su cui giace il segmento. Un segmento può avere al massimo due prolungamenti, poiché ci sono solo due estremi da cui è prolungabile. Per la semiretta ci sarà un solo prolungamento che parte dall’origine e avente direzione data dalla retta su cui la semiretta giace.
Nel proporre ai bambini i concetti di prolungamento di un segmento e di una semiretta, è importante non utilizzare un linguaggio troppo formale, almeno non in un primo momento. Si deve trovare un compromesso didattico per evitare complicazioni accessorie e gli approfondimenti avverranno a tempo debito.
Angolo convesso e angolo concavo
Dopo aver introdotto la nozione di prolungamento di un segmento e di una semiretta, possiamo finalmente addentrarci nella caratterizzazione degli angoli convessi e degli angoli concavi.

Angolo concavo e angolo convesso – YouTube
Angoli convessi
Un angolo è convesso se non contiene i prolungamenti dei propri lati, o più precisamente delle semirette che lo individuano. Ciò significa che, se prolunghiamo i lati dell’angolo, le semirette ottenute non devono intersecare l’angolo stesso.
Ad esempio, consideriamo i tre angoli nella figura seguente:
Chiediamo agli alunni se notano qualche caratteristica comune ai tre angoli. La proprietà che li accomuna non è l’ampiezza, ma il fatto che non contengono i prolungamenti dei propri lati. Quindi, i tre angoli sono tutti angoli convessi.
Per verificare se un angolo è convesso, possiamo prolungare i suoi lati e verificare se i prolungamenti invadono l’angolo stesso. Se i prolungamenti non intersecano l’angolo, allora esso è convesso.
Angoli concavi
Un angolo è concavo se contiene almeno uno dei prolungamenti dei propri lati, o più precisamente delle semirette che lo individuano. Ciò significa che, se prolunghiamo i lati dell’angolo, almeno una delle semirette ottenute interseca l’angolo stesso.
Ad esempio, consideriamo l’angolo nella figura seguente:
In questo caso, se prolunghiamo il lato verde, la semiretta ottenuta interseca l’angolo stesso, quindi l’angolo è concavo.
Angoli concavi
Gli angoli concavi sono un’altra famiglia di angoli in geometria, diversi dagli angoli convessi.
Definizione di angolo concavo
Un angolo concavo è un angolo che contiene almeno uno dei prolungamenti dei propri lati, o più precisamente delle semirette che lo individuano.
Per identificare un angolo concavo, possiamo prolungare i suoi lati e verificare se i prolungamenti intersecano l’angolo stesso. Se almeno uno dei prolungamenti invadono l’angolo, allora esso è concavo.
Esempio di angolo concavo
Ad esempio, consideriamo l’angolo nella figura seguente:
In questo caso, se prolunghiamo il lato verde e il lato rosso, otteniamo dei prolungamenti che invadono l’angolo stesso. Quindi, l’angolo è concavo.
Utilità degli angoli concavi in geometria
Gli angoli concavi sono utili in geometria per definire figure complesse come i poligoni concavi.
Per maggiori informazioni sull’argomento, si può consultare la seguente fonte: https://it.wikipedia.org/wiki/Angolo_concavo
Stai guardando: ANGOLO CONCAVO E CONVESSO