ROMBO

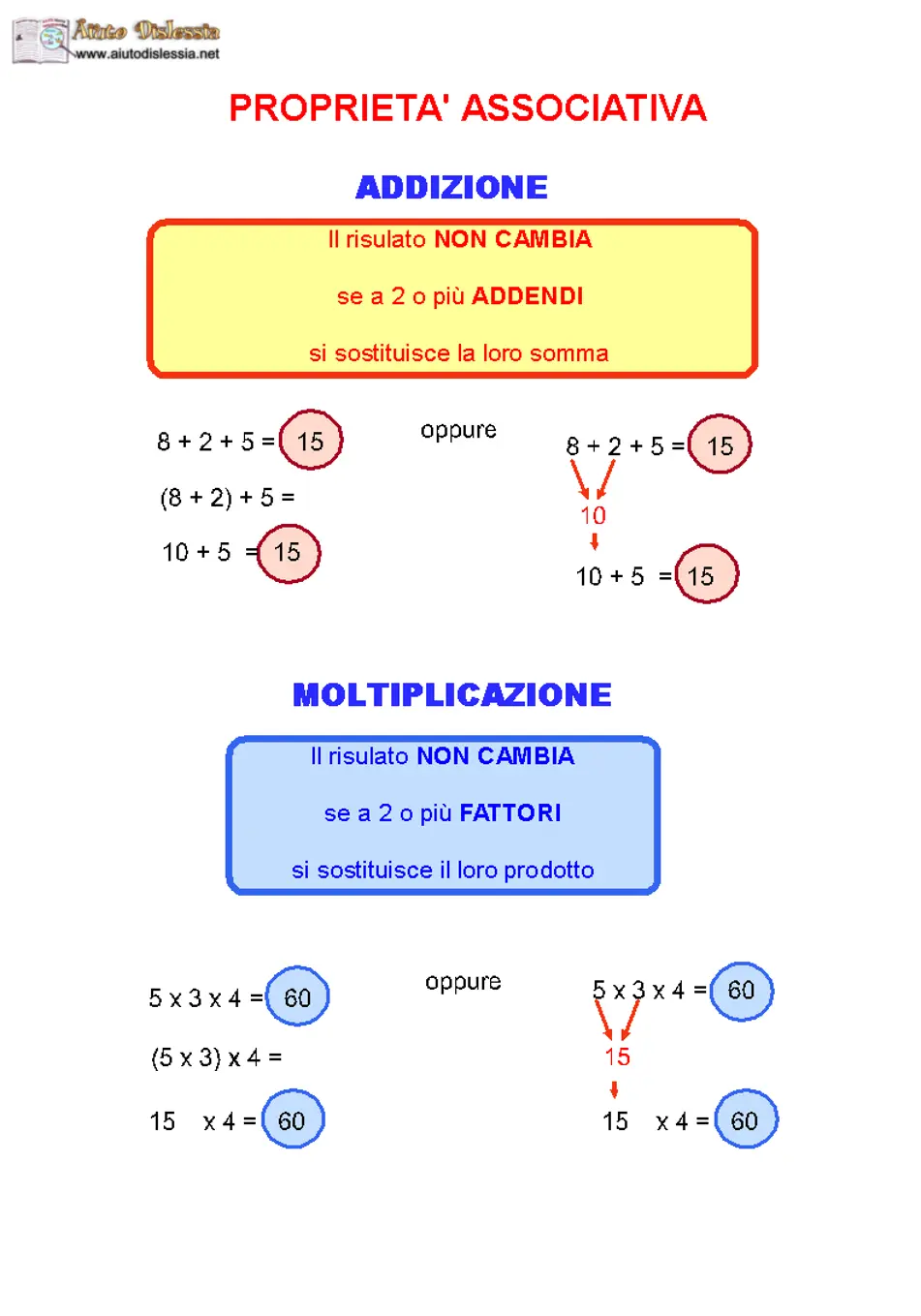
Il rombo è un quadrilatero convesso con i lati congruenti, il che significa che ha quattro lati di uguale lunghezza e i lati opposti sono paralleli. La pagina fornisce tutte le informazioni necessarie sul rombo, tra cui le formule e le proprietà.

È possibile trovare un elenco completo delle formule del rombo, che sono utili per risolvere i problemi e gli esercizi. Inoltre, vengono spiegate la definizione di rombo e tutte le proprietà che lo caratterizzano, come le misure dei lati e degli angoli, le relazioni con le altre figure geometriche piane e le proprietà di simmetria.
Geometria: Definizione di Rombo
Il rombo è una figura piana della Geometria che si definisce come un quadrilatero convesso equilatero. Vediamo di analizzare la definizione in dettaglio.
Quadrilatero Convesso
Un quadrilatero è una figura piana che ha quattro lati. Il rombo, quindi, ha quattro lati che possono avere lunghezze differenti ma che non si intrecciano tra loro. In altre parole, il rombo è un quadrilatero convesso, ovvero non presenta nessuna concavità verso l’esterno.
Equilatero
Il rombo ha un’altra importante proprietà: è equilatero, cioè ha i lati tutti congruenti tra loro. Questa proprietà implica che il rombo è anche un quadrilatero equiangolo, ovvero ha gli angoli tutti congruenti tra loro.

Conclusioni
In sintesi, il rombo è una figura piana con quattro lati, tutti congruenti tra loro e con gli angoli tutti congruenti tra loro.
Rambo First Blood 2 (1985) – Helicopter Vs Helicopter Scene (1080p) FULL HD – YouTube
Geometria: Formule del Rombo
Il rombo è una figura geometrica piana che possiede alcune formule specifiche per il calcolo del perimetro, dell’area, delle diagonali, dell’altezza, del raggio e dei lati.
Simboli utilizzati
Per semplificare la comprensione delle formule del rombo, si utilizzano alcuni simboli specifici:
- L: lato del rombo
- d1: diagonale maggiore
- d2: diagonale minore
- 2p: perimetro del rombo
- A: area del rombo
- h: altezza del rombo
- r: raggio della circonferenza inscritta nel rombo
Elenco delle formule
Ecco un elenco delle formule più importanti del rombo:
- Perimetro del rombo: 2p = 4L
- Lato (con il perimetro): L = (2p)/(4)
- Area del rombo (con diagonali): A = (d1×d2)/(2)
- Diagonale maggiore: d1 = (2A)/(d2)
- Diagonale minore: d2 = (2A)/(d1)
- Area del rombo (con altezza e lato): A = L×h
- Lato (con l’area): L = (A)/(h)
- Altezza (con l’area): h = (A)/(L)
- Area del rombo (con lato e raggio): A = L×2r
- Lato (con il raggio): L = (A)/(2r)
- Raggio della circonferenza inscritta: r = (A)/(2L)
- Altezza (con il raggio): h = 2r
- Raggio (con l’altezza): r = (h)/(2)
- Lato con le diagonali (teorema di Pitagora): L = √(((d1)/(2))^2+((d2)/(2))^2)
- Semi-diagonale maggiore: (d1)/(2) = √(L^2-((d2)/(2))^2)
- Semi-diagonale minore: (d2)/(2) = √(L^2-((d1)/(2))^2)
Conclusioni
Il rombo è una figura geometrica molto interessante e le sue formule sono molto utili per risolvere esercizi di Geometria piana. È importante conoscerle e saperle applicare correttamente per ottenere risultati precisi e affidabili.
Geometria: Proprietà del Rombo
Il rombo è una figura geometrica piana molto interessante e possiede diverse proprietà che lo distinguono dagli altri quadrilateri. Ecco un elenco completo delle proprietà del rombo:
Proprietà dei lati e degli angoli
- I lati di un rombo sono tutti congruenti tra loro, dunque il rombo è equilatero.
- I lati opposti sono paralleli.
- In un rombo gli angoli opposti sono congruenti e gli angoli consecutivi sono supplementari.
- La somma degli angoli interni di un rombo è uguale a un angolo giro.

Proprietà delle diagonali
- Un rombo ha 8 altezze tutte congruenti tra loro. Da ogni vertice si possono tracciare due altezze, che a seconda dei casi possono cadere perpendicolarmente sul lato opposto oppure sul suo prolungamento.
- Un rombo ha le diagonali perpendicolari.
- Le diagonali di un rombo si incontrano in un punto, detto centro del rombo, che le divide entrambe in due segmenti congruenti.
- Ciascuna diagonale divide il rombo in due triangoli isosceli.
- Le diagonali di un rombo formano quattro triangoli rettangoli, congruenti tra loro e ciascuno con i cateti dati dalle semidiagonali del rombo.
- Le diagonali di un rombo sono bisettrici degli angoli interni.
Proprietà di simmetria e circoscrivibilità
- Un rombo ha 2 assi di simmetria, dati dalle sue diagonali.
- Il centro del rombo è il suo centro di simmetria.
- Poiché le somme delle misure dei lati opposti sono uguali (condizione di circoscrivibilità dei quadrilateri), è sempre possibile inscrivere una circonferenza in un rombo. Il centro della circonferenza inscritta coincide con il centro del rombo.
Tipi di rombo particolari
- Un quadrato è un rombo con i quattro angoli congruenti (90°).
Conclusioni
Il rombo è una figura geometrica piana molto importante e ha diverse proprietà che lo caratterizzano. È fondamentale conoscerle e saperle applicare correttamente per risolvere problemi e esercizi di Geometria piana.
Fonte: https://www.tutorvista.com/math/rhombus-properties
Stai guardando: ROMBO