PROPORZIONI
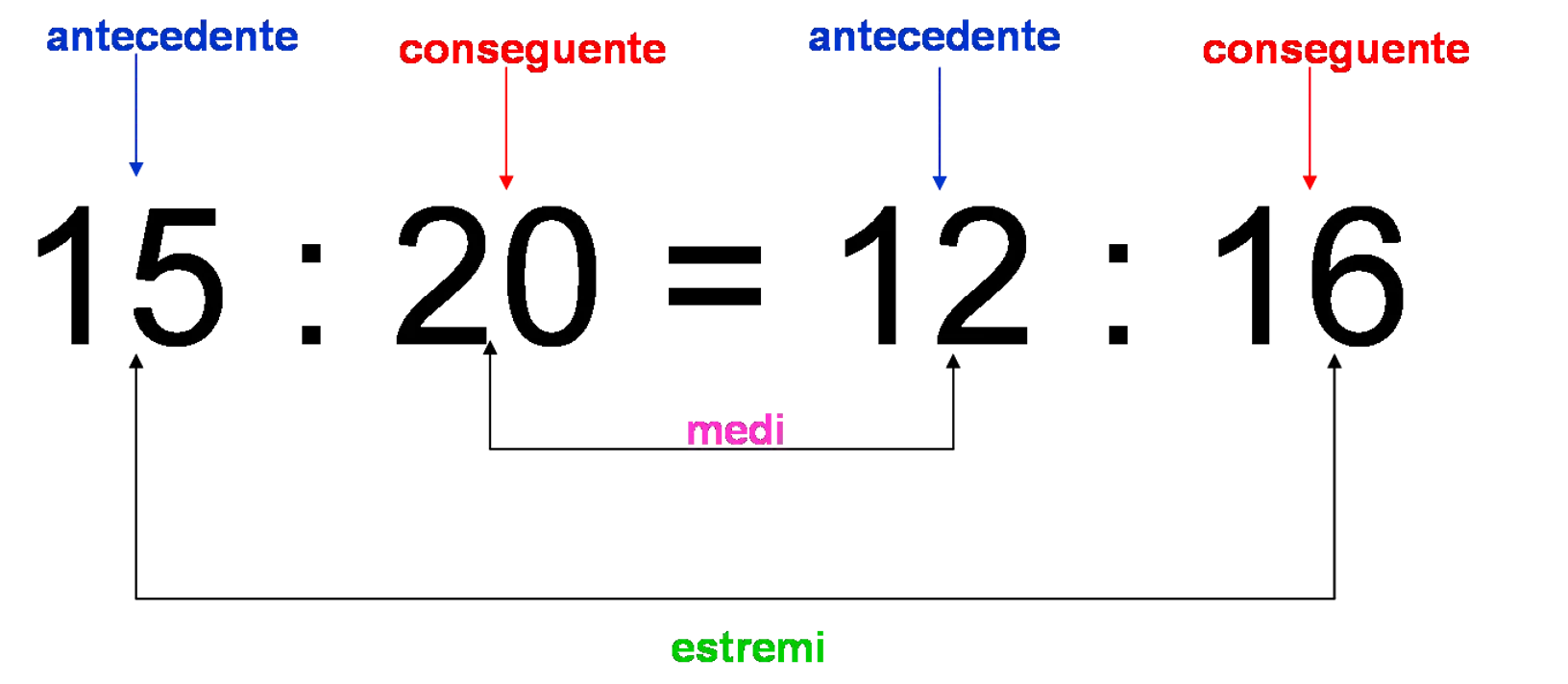
Una proporzione è un’uguaglianza tra il rapporto di due grandezze ed il rapporto di altre due grandezze, espressa nella forma a:b=c:d, dove a, b, c e d sono numeri. Le proporzioni coinvolgono quattro grandezze e soddisfano alcune proprietà che permettono di effettuare i calcoli con le quantità coinvolte. Quando si dice che due grandezze sono proporzionali tra loro, significa che esse seguono una proporzione.

Nella pratica, le proporzioni sono utilizzate per risolvere problemi che coinvolgono grandezze proporzionali, come ad esempio la regola di tre semplice, che permette di calcolare una quantità ignota partendo da altre tre quantità note. Le proporzioni sono presenti anche nella vita di tutti i giorni, ad esempio quando si devono dosare gli ingredienti per una ricetta o calcolare i tempi di percorrenza in un viaggio in auto.
La definizione di proporzione
In matematica, una proporzione è un’uguaglianza tra due rapporti. Questa relazione è espressa come:
(a)/(b) = (c)/(d)
Dove a, b, c, e d sono quattro numeri, quantità o grandezze. Questa uguaglianza indica che il rapporto tra a e b è uguale al rapporto tra c e d.
Un’altra forma di espressione della proporzione è attraverso i due punti:
a:b = c:d
Questa espressione indica la stessa relazione dell’uguaglianza precedente.

Fonte: Math is Fun
Proporzioni – Trovare il termine incognito, Problemi e Proprietà – YouTube
Le proporzioni e il loro significato
Le proporzioni sono un concetto matematico semplice che esprime l’uguaglianza tra due rapporti. Questo significa che due coppie di numeri devono avere lo stesso rapporto tra loro.
Come funzionano le proporzioni
Per esempio, se abbiamo le coppie di numeri (a,b) e (c,d) e scriviamo:
(a)/(b) = (c)/(d)
Questo significa che il rapporto tra a e b è uguale al rapporto tra c e d. Un altro modo di esprimere questa relazione è attraverso l’uso dei due punti:
a:b = c:d
È importante notare che non importa quali siano i numeri a,b,c e d, l’importante è il rapporto tra di essi.
Utilità delle proporzioni nella vita quotidiana
Le proporzioni hanno diverse applicazioni pratiche nella vita quotidiana, ad esempio nella gestione del denaro.
Per esempio, supponiamo di voler capire quanto costa mangiare tre panini, sapendo che ieri abbiamo mangiato due panini per 6 euro. Possiamo usare una proporzione per trovare la risposta. Scriviamo:
6:2 = x:3
Dove x è il costo dei tre panini. Dato che i due rapporti devono coincidere, possiamo risolvere l’equazione:
(6)/(2) = (x)/(3)
Da cui si ottiene:
x = 3×3 = 9
Quindi, dovremmo pagare 9 euro per tre panini.
Le proprietà delle proporzioni
Le proporzioni hanno alcune proprietà importanti che ne semplificano la risoluzione. Prima di tutto, è utile definire i termini “estremi proporzionali” e “medi proporzionali”. Gli estremi proporzionali sono i due numeri più esterni rispetto all’uguale, mentre i medi proporzionali sono i due numeri più vicini all’uguale.
Le proprietà delle proporzioni
Se abbiamo una proporzione a:b = c:d, allora valgono le seguenti proprietà:
Proprietà fondamentale:
a×d = b×c
Proprietà dell’invertire:
b:a = d:c
Permutare i medi:
a:c = b:d
Permutare gli estremi:
d:b = c:a
Proprietà del comporre:
(a+b):b = (c+d):d ; (a+b):a = (c+d):c
Proprietà dello scomporre (se a > b):
(a-b):b = (c-d):d ; (a-b):a = (c-d):c
Proprietà del comporre e permutare:
(a+b):(a-b) = (c+d):(c-d)
Queste proprietà possono semplificare la risoluzione delle proporzioni e consentono di passare da una forma all’altra.
Fonte: Matematika
Come risolvere gli esercizi sulle proporzioni con l’incognita x
Per risolvere un esercizio sulle proporzioni con un’incognita x, dobbiamo impostare una proporzione che coinvolga le grandezze note e l’incognita.
Supponiamo che la proporzione sia della forma:
a:x = b:c
Per trovare il valore di x, dobbiamo utilizzare la proprietà fondamentale delle proporzioni, che ci dice che:
a×c = x×b
Per trovare il valore di x, dobbiamo quindi riscrivere la proporzione come:
x = (a×c)/(b)
In questo modo, possiamo trovare il valore dell’incognita x.
Ad esempio, supponiamo che abbiamo la proporzione:
2:x = 6:3
Per trovare il valore di x, applichiamo la proprietà fondamentale:
2×3 = x×6
Riscrivendo l’equazione, otteniamo:
x = (2×3)/6 = 1
Quindi, x = 1.
Esempio di applicazione delle proporzioni per risolvere un problema
Le proporzioni possono essere utilizzate per risolvere una vasta gamma di problemi matematici. Ad esempio, consideriamo il seguente problema:
Un operaio ha bisogno di 14400 euro per comprare una macchina. Se guadagna 540 euro in 3 giorni, quanti giorni dovrà lavorare per raggiungere la cifra necessaria?
Per risolvere questo problema, dobbiamo impostare una proporzione che coinvolga le grandezze note e l’incognita. Supponiamo che la proporzione sia della forma:
540 euro : 3 giorni di lavoro = 14400 euro : x giorni di lavoro
Dove x è il numero di giorni necessari per raggiungere la cifra di 14400 euro.
Per trovare il valore di x, dobbiamo utilizzare la proprietà fondamentale delle proporzioni:
540×x = 3×14400
Dividendo entrambi i membri per 540, otteniamo:
x = (3×14400)/(540) = 80
Quindi, l’operaio dovrà lavorare 80 giorni per raggiungere la cifra di 14400 euro necessaria per acquistare la macchina.
Fonte: YouMath
Stai guardando: PROPORZIONI