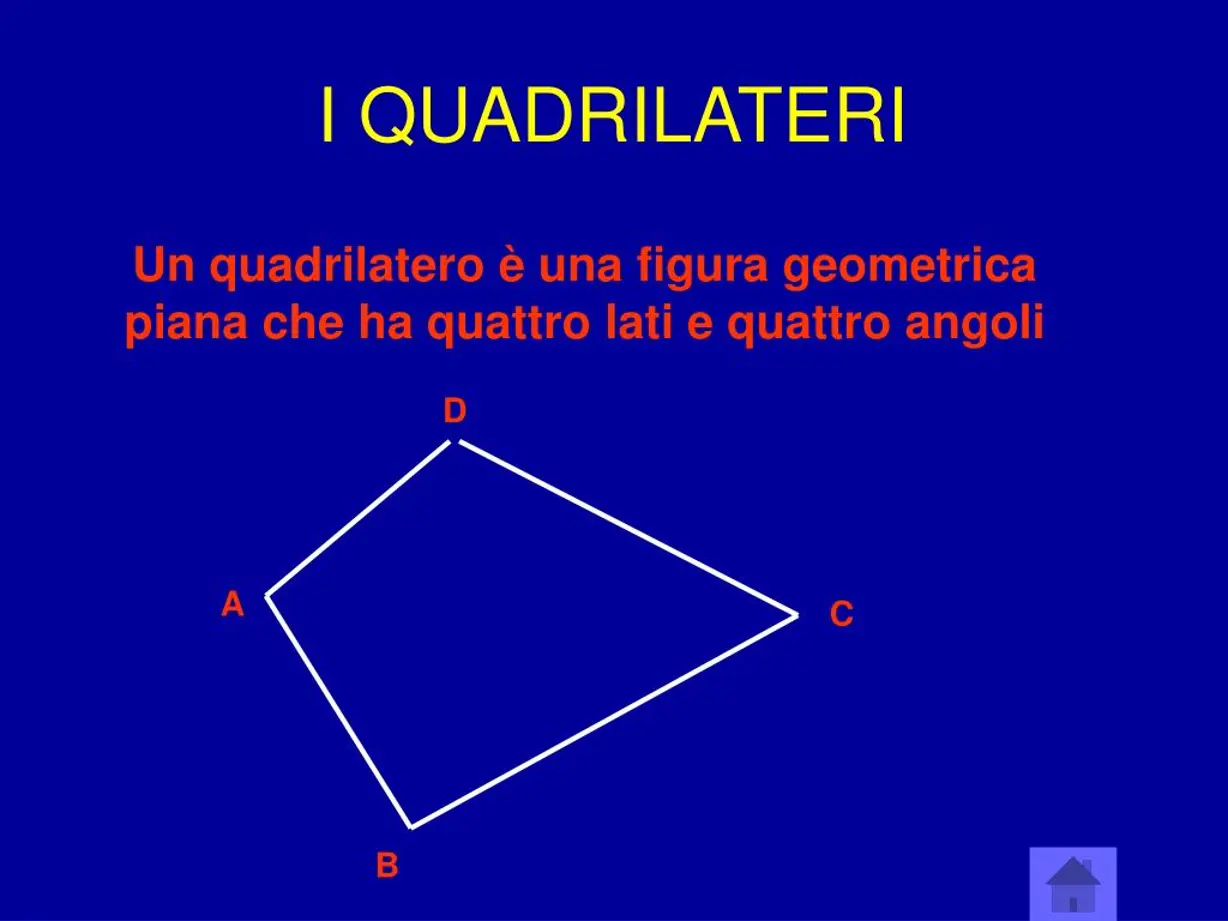
QUADRILATERI

In Geometria, un quadrilatero è un poligono costituito da quattro lati. I quadrilateri possono essere semplici o complessi. I quadrilateri semplici si distinguono in base all’intreccio dei loro lati e si dividono ulteriormente in due categorie: concavi e convessi. I quadrilateri complessi, invece, hanno lati che si intrecciano tra loro. I quadrilateri convessi non contengono alcun prolungamento dei loro lati, mentre i quadrilateri concavi lo fanno.

Definizione di quadrilatero
Un quadrilatero (convesso) è un poligono (convesso) costituito da quattro lati.
Formule del Quadrilatero
In geometria piana, un quadrilatero è una figura geometrica formata da quattro lati e quattro vertici. Esistono diverse formule utilizzate per calcolare le proprietà dei quadrilateri, come il perimetro e l’area.
Significato dei simboli utilizzati
Prima di presentare le formule del quadrilatero, è importante specificare il significato dei simboli utilizzati.
- A, B, C, D: i vertici del quadrilatero, ossia i punti di incontro dei lati
- 2p: il perimetro del quadrilatero
- p: il semiperimetro del quadrilatero
- S: l’area del quadrilatero
- r: il raggio della circonferenza inscritta
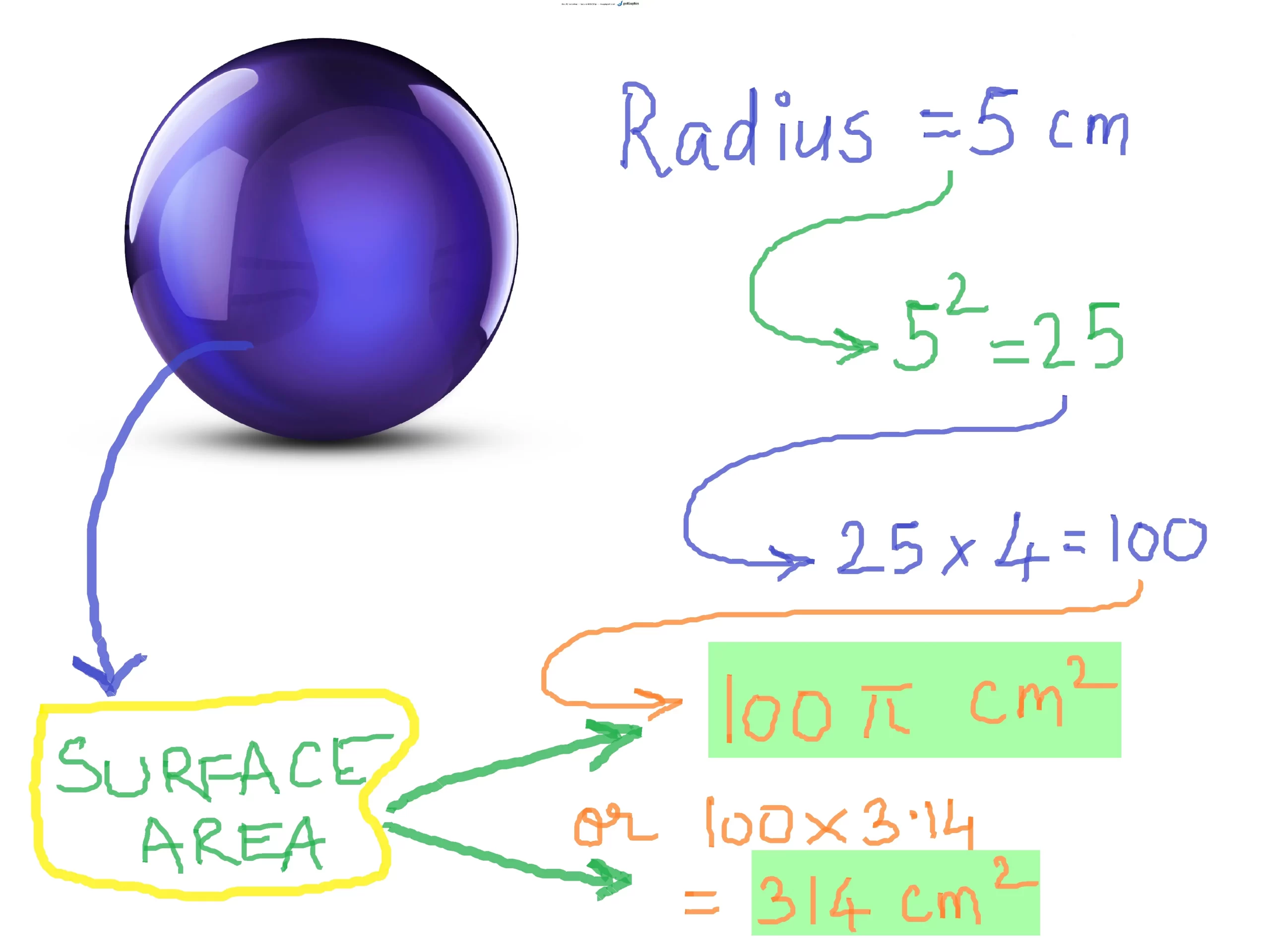
Perimetro del quadrilatero
Il perimetro del quadrilatero si calcola sommando la lunghezza dei quattro lati:
2p = AB + BC + CD + DA
Definizione e proprietà dei quadrilateri – Geometria – Secondaria di Primo Grado – YouTube
Area del quadrilatero
Esistono diverse formule per calcolare l’area di un quadrilatero, a seconda delle sue caratteristiche. Una delle formule più generiche è la formula di Brahmagupta, che si applica solo ai quadrilateri inscrivibili:
S = √((p-AB)(p-BC)(p-CD)(p-DA))
È possibile calcolare l’area del quadrilatero anche considerando una delle diagonali e sommando le aree dei due triangoli corrispondenti.
Fonte: YouMath
Teoremi e proprietà del quadrilatero
Somma degli angoli interni
La somma degli angoli interni di un quadrilatero è sempre uguale a un angolo giro (360°).
Disuguaglianza triangolare
La misura di ciascun lato di un quadrilatero è minore della somma delle misure degli altri lati.
Quadrilatero circoscrivibile
Un quadrilatero è circoscrivibile a una circonferenza se le somme delle misure delle coppie di lati opposti si equivalgono:
AB + CD = BC + DA
Quadrilatero inscrivibile
Un quadrilatero è inscrivibile in una circonferenza se e solo se gli angoli opposti sono supplementari:
A + C = B + D
Teorema di Tolomeo
Il teorema di Tolomeo per quadrilateri inscrivibili in una circonferenza afferma che il prodotto delle misure delle diagonali è uguale alla somma dei prodotti delle misure delle due coppie di lati opposti del quadrilatero:
AC×BD = AB×CD + BC×AD
Teorema di Legendre
Il teorema di Legendre per quadrilateri inscrivibili in una circonferenza afferma che il rapporto tra le misure delle due diagonali è uguale al rapporto tra le somme dei prodotti dei lati consecutivi che concorrono nei vertici delle rispettive diagonali:
(AC)/(BD) = (AB×BC+AD×DC)/(AB×AD+BC×DC)
Raggio della circonferenza circoscritta
Il raggio della circonferenza circoscritta a un quadrilatero si può calcolare con la seguente formula:
r = (√((AB×DC+AD×BC)×(AB×BC+AD×DC)×(AB×AD+BC×DC)))/(4S)
Formule per l’area del quadrilatero
Oltre alla formula di Brahmagupta per i quadrilateri inscrivibili, esistono altre due formule per calcolare l’area di un quadrilatero qualsiasi: la formula di Bretschneider e la formula delle diagonali. Poiché entrambe richiedono di conoscere nozioni trigonometriche, le abbiamo trattate in un approfondimento separato sull’area del quadrilatero.
Classificazione dei quadrilateri
Esistono diversi tipi di quadrilateri particolari:
- Il trapezio è un quadrilatero convesso con due lati paralleli.
- Il parallelogramma è un quadrilatero convesso con i lati a due a due paralleli.
- Il rombo è un quadrilatero convesso con i lati congruenti.
Stai guardando: QUADRILATERI