FRAZIONE GENERATRICE
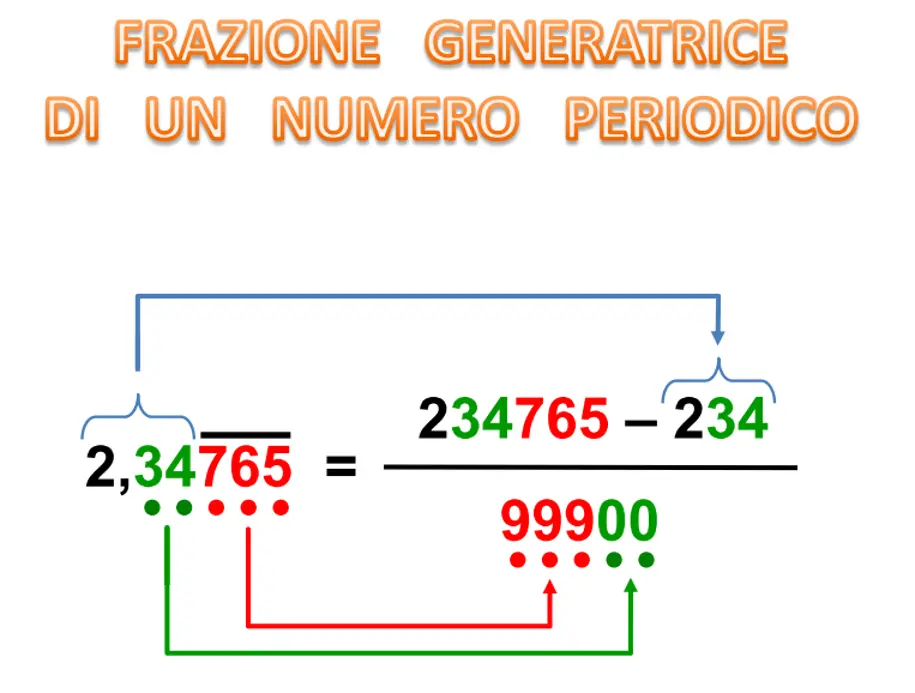
Un numero decimale può essere espresso come una frazione generatrice, dove il numeratore diviso il denominatore dà come risultato il numero decimale iniziale. Ci sono diverse regole per trasformare un numero decimale in una frazione generatrice e dipendono dal tipo di numero decimale.

In questa lezione, esamineremo come si possono scrivere le frazioni generatrici dei numeri decimali e capiremo anche come determinare il tipo di numero decimale, semplicemente osservando il denominatore di una frazione qualsiasi.
Frazione generatrice di un numero decimale
La frazione generatrice di un numero decimale rappresenta la frazione equivalente al numero decimale. Questa può essere ricavata applicando regole diverse, a seconda del tipo di numero decimale di cui si tratta.
È possibile distinguere tra numeri decimali limitati e numeri decimali periodici. Nel caso di numeri decimali limitati, la parte decimale ha un numero finito di cifre dopo la virgola, mentre nei numeri decimali periodici, una o più cifre decimali si ripetono all’infinito.
Frazione generatrice di un numero decimale limitato
Per determinare la frazione generatrice di un numero decimale limitato, si deve scrivere una frazione avente:
- come numeratore il numero senza virgola;
- come denominatore un 1 seguito da tanti zeri quante sono le cifre decimali.
Ad esempio, la frazione generatrice di 1,01 è (101)/(100), la frazione generatrice di 0,11 è (11)/(100) e la frazione generatrice di 32,1 è (321)/(10).
Frazione generatrice di un numero decimale periodico semplice
La frazione generatrice di un numero decimale periodico semplice è una frazione avente:
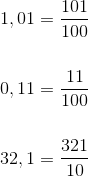
- al numeratore la differenza tra l’intero numero scritto senza la virgola e la parte intera;
- al denominatore tanti nove quante sono le cifre che compongono il periodo.
Ad esempio, la frazione generatrice di 22,3 è (201)/(9), la frazione generatrice di 0,29 è (29)/(99) e la frazione generatrice di 1,213 è (404)/(333).
Frazioni generatrici – YouTube
Frazione generatrice di un numero decimale periodico misto
La frazione generatrice di un numero decimale periodico misto rappresenta la frazione equivalente al numero decimale misto, ovvero un numero formato da una parte intera e una parte decimale periodica. Per calcolare la frazione generatrice di un numero decimale periodico misto si deve scrivere una frazione avente:
- come numeratore la differenza tra l’intero numero senza virgola e tutto ciò che non fa parte del periodo;
- come denominatore tanti nove quante sono le cifre che compongono il periodo, seguiti da tanti zeri quanti sono le cifre dell’antiperiodo.
Ad esempio, la frazione generatrice di 2,23 è (67)/(30), la frazione generatrice di 0,23 è (7)/(30) e la frazione generatrice di 1,213 è (91)/(75).
È importante notare che per i numeri decimali illimitati non periodici non esiste una frazione generatrice in quanto tali numeri sono irrazionali. I numeri irrazionali sono tutti i numeri con la virgola che non possono essere espressi sotto forma di frazione, contrariamente ai numeri razionali che sono i numeri esprimibili sotto forma di frazioni.
Dalla frazione generatrice al numero decimale
Per convertire una frazione in un numero decimale, si deve eseguire la divisione tra il numeratore e il denominatore della frazione. Tuttavia, è possibile stabilire in anticipo il tipo di numero decimale che sarà generato dalla frazione.
Per fare ciò, la frazione deve essere ridotta ai minimi termini, e:
- se il denominatore è 1, allora la frazione genera un numero intero (un caso particolare di frazione apparente).
- se il denominatore è diverso da 1, lo si scompone in fattori primi e si osservano i fattori della scomposizione:
- se tra i fattori appaiono solo 2 e 5, allora la frazione genera un numero decimale limitato.
- se tra i fattori non appaiono né il 2 né il 5, allora la frazione genera un numero decimale illimitato periodico semplice.
- se tra i fattori della scomposizione appaiono altri numeri primi oltre al 2 o al 5, allora la frazione genera un numero decimale illimitato periodico misto.
Conoscere il tipo di numero decimale generato da una frazione può essere utile per stabilire se il numero decimale sarà finito o periodico e, nel caso di numeri periodici, se il periodo è semplice o misto.
Fonte: Wikipedia
Esempi sul tipo di numero decimale che genera una frazione
Di seguito sono riportati alcuni esempi su come determinare il tipo di numero decimale che una frazione genera.
Esempio 1
Determinare che tipo di numero decimale genera la frazione (12)/(32).
Riduciamo la frazione ai minimi termini dividendo numeratore e denominatore per 4: (12)/(32) = (3)/(8). Il denominatore è 8, scomposto in fattori primi diventa 8 = 2×2×2 = 2^3. Nella scomposizione appare solo il fattore 2, quindi il numero generato dalla frazione è un numero decimale limitato.
Verifichiamo eseguendo la divisione in colonna tra 12 e 32:
| 0, | 3 | 7 | 5 | ||
| 32 | | | 1 | 2 | ||
| 2 | 4 | ||||
| – | 8 | ||||
| 2 | 1 | ||||
| – | |||||
| 0, | 3 | ||||
Pertanto, 12/32 = 0,375 ed è un numero decimale limitato.
Esempio 2
Stabilire che tipo di numero genera la frazione (18)/(9).
Riduciamo la frazione ai minimi termini dividendo numeratore e denominatore per 9: (18)/(9) = (2)/(1) = 2. Il denominatore è 1, quindi la frazione genera un numero intero (la frazione è apparente).
Esempio 3
Determinare che tipo di numero genera la frazione (12)/(18).
Riduciamo la frazione ai minimi termini dividendo numeratore e denominatore per 6: (12)/(18) = (2)/(3). Il denominatore è 3 ed è già scomposto in fattori primi. Non appaiono né 2 né 5, quindi la frazione genera un numero decimale illimitato periodico semplice. Verifichiamo con l’aiuto della calcolatrice: 2/3 = 0,666666666… = 0,6.
Esempio 4
Prima di eseguire la divisione tra numeratore e denominatore, stabilire che tipo di numero decimale genera la frazione (2)/(12).
Dividendo numeratore e denominatore per 2 riduciamo la frazione ai minimi termini:
Stai guardando: FRAZIONE GENERATRICE