AREA DEL TRIANGOLO: TUTTE LE FORMULE CON ESEMPI SVOLTI
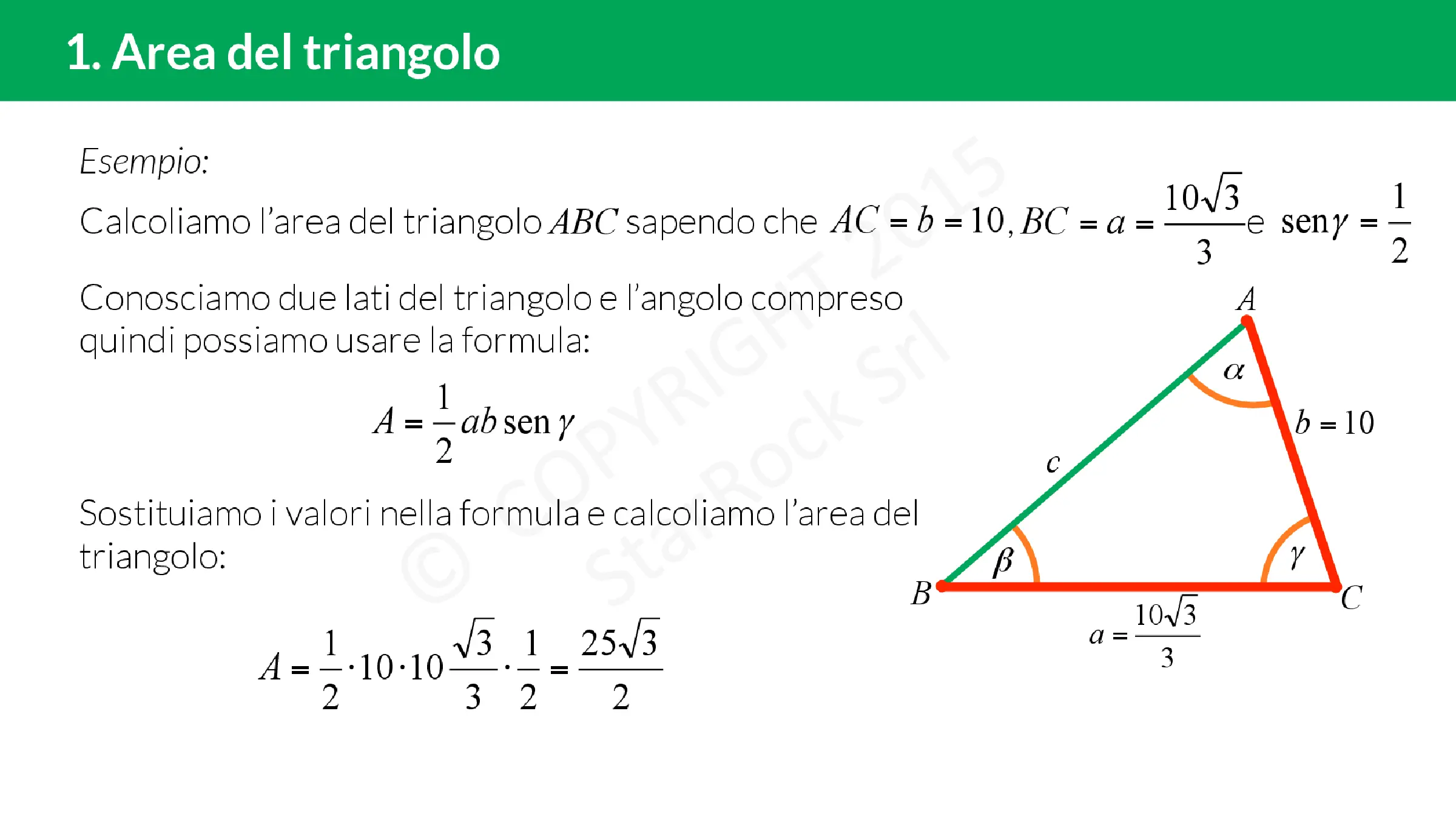
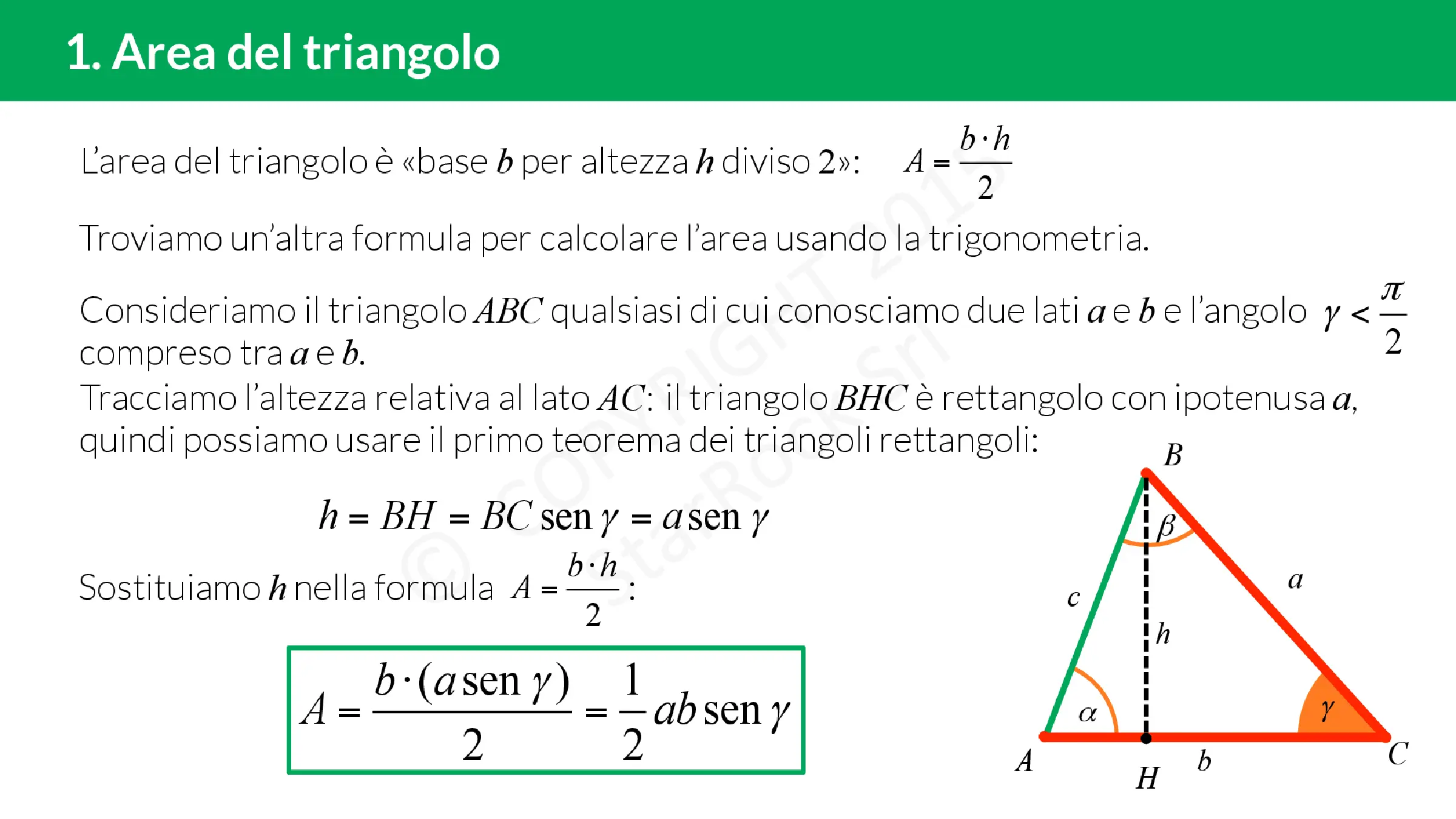
L’area di un triangolo può essere calcolata in vari modi. Una delle formule più comuni è A = b · h / 2, dove b rappresenta la base e h l’altezza relativa ad essa. Questa formula è applicabile a qualsiasi tipo di triangolo. In generale, l’area di un triangolo può essere calcolata moltiplicando la misura di un lato qualsiasi per la misura dell’altezza relativa a esso e dividendo il prodotto per 2.

In alternativa, se si conoscono le misure dei tre lati del triangolo, si può utilizzare la formula di Erone per calcolare l’area. In ogni caso, l’area di un triangolo rappresenta la misura della superficie racchiusa tra i suoi tre lati.
Formule per il calcolo dell’area di un triangolo
Il calcolo dell’area di un triangolo può essere effettuato utilizzando diverse formule, a seconda delle informazioni disponibili sui lati e sulle altezze del triangolo stesso. In questa guida forniremo le formule per il calcolo dell’area di un triangolo qualsiasi, equilatero e rettangolo.
Triangolo qualsiasi
Per il calcolo dell’area di un triangolo qualsiasi, possiamo utilizzare due formule differenti:
- S = (AB × hC) / 2
- S = √(p × (p – AB) × (p – BC) × (p – AC))
Dove S rappresenta l’area del triangolo, AB, BC e AC le misure dei lati, p il semiperimetro e hC l’altezza relativa al lato BC.
Triangolo equilatero
Per il calcolo dell’area di un triangolo equilatero, possiamo utilizzare diverse formule, a seconda delle informazioni disponibili:
- S = (√3 / 4) × L2, dove L è il lato del triangolo
- S = H2 / (√3), dove H è l’altezza del triangolo
- S = (√3 / 36) × (2p)2, dove 2p è il perimetro del triangolo
- S = 3√3 × r2, dove r è l’apotema del triangolo
- S = (3√3 / 4) × R2, dove R è il raggio della circonferenza circoscritta al triangolo
L’area del triangolo – Geometria – Secondaria di Primo Grado – YouTube
Triangolo rettangolo
Per il calcolo dell’area di un triangolo rettangolo, possiamo utilizzare due formule differenti:
- S = (c1 × c2) / 2, dove c1 e c2 sono i cateti del triangolo
- S = (i × h) / 2, dove i è l’ipotenusa del triangolo e h è l’altezza relativa all’ipotenusa
Queste sono le formule per il calcolo dell’area di un triangolo, suddivise per tipo di triangolo. È importante ricordare che per il triangolo scaleno e per il triangolo isoscele non esistono formule particolari, ma valgono le formule per il triangolo qualsiasi.
Esercizi svolti sull’area del triangolo
In questa sezione vediamo alcuni esercizi svolti sull’area del triangolo qualsiasi, per comprendere come applicare le formule per il calcolo dell’area elencate nella tabella.
Esercizio 1
Dato un triangolo con base di lunghezza 12 cm e altezza relativa alla base pari alla metà della base aumentata di 3 cm, calcolare l’area del triangolo.
Svolgimento: indicando con AB la base e con hC l’altezza, abbiamo che AB = 12 cm e hC = 1/2 × AB + 3 cm. Possiamo quindi calcolare l’altezza del triangolo:
hC = 1/2 × AB + 3 cm = 1/2 × 12 cm + 3 cm = 6 cm + 3 cm = 9 cm
Infine, calcoliamo l’area del triangolo:
S = (AB × hC) / 2 = (6 cm × 9 cm) / 2 = 54 cm2 / 2 = 27 cm2
Esercizio 2
Dato un triangolo con perimetro di 60 decimetri e due lati di lunghezza 20 dm e 25 dm, calcolare l’area del triangolo.
Svolgimento: indichiamo con AB, AC e BC i lati del triangolo. Sappiamo che AB = 20 dm e AC = 25 dm. Possiamo calcolare la lunghezza del lato BC:
BC = perimetro – AB – AC = 60 dm – 20 dm – 25 dm = 15 dm
Calcoliamo quindi il semiperimetro:
p = perimetro / 2 = 60 dm / 2 = 30 dm
Infine, calcoliamo l’area del triangolo con la formula di Erone:
S = √(p × (p – AB) × (p – BC) × (p – AC)) = √(30 dm × 10 dm × 15 dm × 5 dm) = √22500 dm4 = 150 dm2
Fonte: Matematika.it
Stai guardando: AREA DEL TRIANGOLO: TUTTE LE FORMULE CON ESEMPI SVOLTI