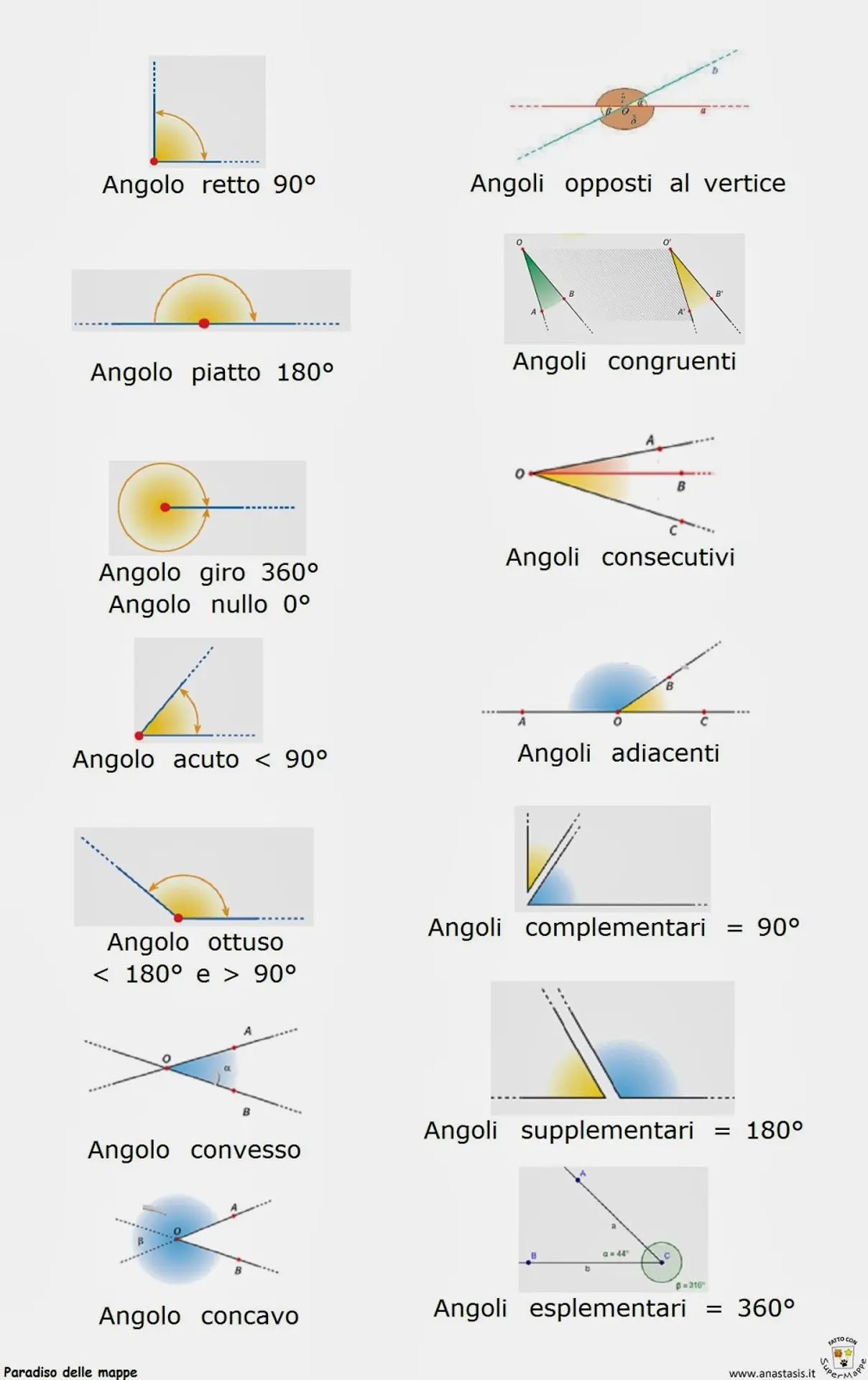
RADICE QUADRATA

La radice quadrata di un numero, anche detta radice con indice 2, è un numero non negativo che elevato alla seconda restituisce il radicando. È importante sottolineare che la radice quadrata può essere calcolata solo di un numero positivo o nullo, e rappresenta l’operazione inversa dell’elevamento a seconda.

Questa operazione viene affrontata di solito per la prima volta durante lo studio del teorema di Pitagora. Quindi, in sintesi, la radice quadrata è una funzione matematica che restituisce un valore non negativo che, una volta elevato alla seconda, dà come risultato il radicando.
Calcolo della radice quadrata di un numero naturale
La radice quadrata di un numero naturale si calcola trovando il numero positivo o nullo che, elevato alla seconda potenza, dà come risultato il numero di partenza, ovvero il radicando. In pratica, la radice quadrata di un numero n si indica con il simbolo √n, omettendo generalmente l’indice 2 sopra al segno di radice.
Esempi di calcolo della radice quadrata
Ad esempio, la radice quadrata di 25 è 5, in quanto 52 = 25. Analogamente, la radice quadrata di 36 è 6, poiché 62 = 36, e la radice quadrata di 121 è 11, perché 112 = 121.
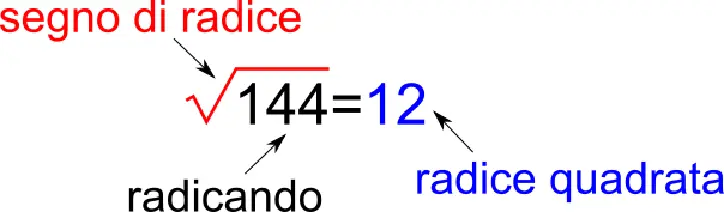
Terminologia della radice quadrata
Il numero di cui si vuole calcolare la radice quadrata è detto radicando, il simbolo della radice quadrata è il segno √, mentre il risultato si chiama radice quadrata.
Fonte: https://it.wikipedia.org/wiki/Radice_quadrata
Radice quadrata di un quadrato perfetto
Un quadrato perfetto è un numero naturale che può essere scritto come il quadrato di un altro numero naturale. Ad esempio, 64, 100, 81 e 49 sono quadrati perfetti, rispettivamente pari a 82, 102, 92 e 72.
La radice quadrata – Algebra – Secondaria di Primo Grado – YouTube
Come riconoscere i quadrati perfetti
Per riconoscere i quadrati perfetti si può scomporre il numero in fattori primi e verificare se il prodotto dei fattori con esponente pari coincide con il numero originale. Ad esempio, 64 = 26, 100 = 22 × 52, 81 = 34 e 49 = 72 sono quadrati perfetti.
Come calcolare la radice quadrata di un quadrato perfetto
La radice quadrata di un quadrato perfetto si ottiene dimezzando gli esponenti dei fattori che compaiono nella scomposizione in fattori primi. Ad esempio, la radice quadrata di 3025, che può essere scritto come 52 × 112, è semplicemente data da 5 × 11 = 55.
Radice quadrata approssimata
Se un numero non è un quadrato perfetto, non esiste una radice quadrata esatta intera. Tuttavia, possiamo scrivere una radice quadrata approssimata all’unità. Ad esempio, per calcolare la radice quadrata di 27, possiamo trovare il numero intero più grande che, elevato alla seconda, non supera 27, ovvero 5, e il numero intero più piccolo che, elevato alla seconda, supera 27, ovvero 6. Quindi, possiamo affermare che la radice quadrata di 27 è un numero compreso tra 5 e 6, ma non possiamo essere più precisi.
Calcolo della radice quadrata decimale
Se vogliamo calcolare la radice quadrata decimale di un numero, come ad esempio √27, possiamo utilizzare una calcolatrice. Il risultato è 5,196152…, ovvero un numero decimale compreso tra 5 e 6. Se invece vogliamo calcolare le cifre decimali senza l’aiuto della calcolatrice, possiamo utilizzare apposite tecniche di calcolo.
Stai guardando: RADICE QUADRATA