RADICALI E PROPRIETÀ DEI RADICALI
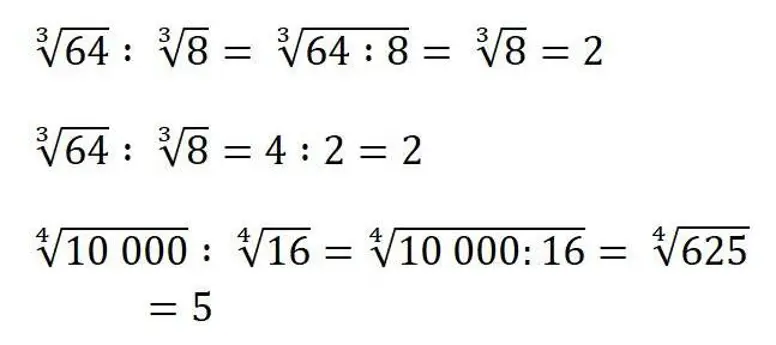
In Matematica, i radicali sono numeri ottenuti mediante l’utilizzo di radici con indice intero. Per semplificare il calcolo dei radicali, è possibile esprimerli come potenze con esponente fratto seguendo una regola semplice. Gli studenti delle scuole superiori potranno trovare in questa lezione tutte le proprietà dei radicali, ma non solo: sarà spiegata anche la condizione di realtà, ovvero la condizione che indica i numeri di cui è possibile calcolare la radice a seconda del segno, e verrà illustrato il collegamento tra radicali e potenze. In breve, si tratta di una lezione completa e dettagliata sul tema dei radicali.
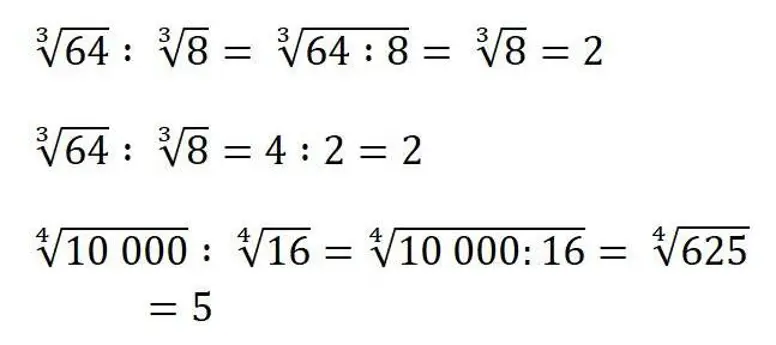
Definizione di radicale
In matematica, la radice n-esima di un numero a è un altro numero b tale che, elevato alla potenza n, ci restituisce il numero a. Il simbolo che rappresenta la radice n-esima è √ e l’indice di radice, che indica la potenza a cui viene elevato il numero b, è n.
Caso n dispari
Se n è un numero dispari, la radice n-esima di a è un numero b che soddisfa la seguente relazione:
[n]√(a) = b ⇔ b^n = a, con a,b ∈ R
In altre parole, la radice n-esima di a è il numero b che elevato alla potenza n restituisce il numero a.
Caso n pari
Se n è un numero pari, la radice n-esima di a è un numero positivo b che soddisfa la seguente relazione:

[n]√(a) = b ⇔ b^n = a, con a ≥ 0, b ≥ 0
In questo caso, poiché esistono numeri negativi il cui quadrato è uguale ad a, si richiede che b sia positivo per evitare ambiguità nella definizione della radice.
Radicali : Operazioni e Principali Proprietà #1 – YouTube
Esempio
Ad esempio, la radice terza di 8 è 2, poiché 2 elevato alla terza potenza è uguale a 8:
[3]√(8) = 2, in quanto 2^(3) = 8
La radice quadrata di 4 è 2, poiché (-2) elevato alla seconda potenza è anch’esso uguale a 4, ma si conviene che la radice quadrata di un numero positivo è il numero positivo che elevato alla seconda potenza restituisce il numero dato.
Per gli studenti della quinta superiore in poi, si precisa che la definizione di funzione radice con indice pari è a valori nell’intervallo [0,+∞) per evitare ambiguità nella definizione della radice.
Fonte: YouMath
Condizione di realtà dei radicali
Un’altra condizione importante da considerare nella definizione dei radicali è la cosiddetta condizione di realtà, che si applica solo nel caso in cui l’indice della radice sia pari. In particolare, il radicando deve essere maggiore o uguale a zero, ovvero a ≥ 0.
Nel caso in cui l’indice della radice sia dispari, invece, il radicando può assumere qualsiasi segno.
È importante notare che la radice quadrata di un numero negativo non è definita, mentre la radice cubica esiste sempre. Ad esempio, [3]√(-64) = -4.
Per capire perché è necessario imporre la condizione di realtà nella definizione dei radicali ad indice pari, consideriamo la definizione stessa:
se n è pari: [n]√(a) = b ⇔ b^n = a, con a ≥ 0, b ≥ 0
Poiché una potenza con esponente pari non può essere negativa, per ogni n pari in b^n = a è necessario richiedere che a sia maggiore di zero (a > 0). Questa condizione è quindi essenziale per far sì che la definizione dei radicali abbia senso.
Radicali come potenze con esponente fratto
Una radice n-esima può essere indicata anche come una potenza con esponente razionale. Infatti, vale la seguente relazione:

[n]√(a) = a(1/n) per ogni n∈N con n ≥ 1
Questa formula ci permette di esprimere la radice ennesima come potenza con esponente razionale. In generale, possiamo scrivere:
[n]√(am) = am/n con n,m∈ N
Per esprimere questa relazione a parole, possiamo dire che l’indice del radicale diventa il denominatore dell’esponente della potenza, mentre l’esponente del radicando diventa il numeratore della potenza.
Tuttavia, dobbiamo fare attenzione agli esponenti negativi. Per definizione, si pone:
a-(m/n): = (1)/[n]√(am)
Ad esempio:
- 25(1/2) = √(25) = 5
- 125(1/3) = [3]√(125) = 5
- 16-(3/4) = (1)/16(3/4) = (1)/[4]√(163) = (1)/8
È importante notare che esprimendo i radicali come potenze, essi ereditano tutte le proprietà delle potenze che conosciamo già.
Proprietà dei Radicali
Somma e differenza di radicali
Le operazioni di somma e differenza tra radicali sono possibili solo se questi sono simili, ovvero se hanno lo stesso indice e lo stesso radicando. In questo caso, la somma/differenza dei radicali è un nuovo radicale che ha lo stesso radicando e come coefficiente la somma dei coefficienti.
Prodotto di radicali con lo stesso indice
Il prodotto di due radicali con lo stesso indice è un nuovo radicale che ha lo stesso indice e come radicando il prodotto dei radicandi.
In altre parole, [n]√(a) × [n]√(b) = [n]√(ab). Il prodotto delle radici n-esime di ogni fattore coincide con la radice n-esima del loro prodotto.
Ad esempio, [3]√(8×27) = [3]√(8)×[3]√(27) = 2×3 = 6.
Quoziente di radicali con lo stesso indice
Il quoziente di due radicali con lo stesso indice è un nuovo radicale che ha come radicando il quoziente dei radicandi e come indice lo stesso indice.
In altre parole, ([n]√(a)) / ([n]√(b)) = [n]√(a/b) (b diverso da 0). Il quoziente delle radici n-esime di ogni fattore coincide con la radice n-esima del loro quoziente.
Radicali con indici diversi
Per calcolare il prodotto o il quoziente di due o più radicali con indici diversi, è necessario utilizzare altre proprietà e formule.
Proprietà invariantiva dei radicali
La proprietà invariantiva dei radicali afferma che, moltiplicando per uno stesso valore l’indice della radice e l’esponente del radicando non negativo, il risultato della radice non cambia. In formule matematiche, questo significa che:
sqrt[n·s]a^(m·s) = [n]√(a^m) ∀ a ≥ 0
La formula può anche essere letta al contrario, da destra a sinistra, se necessario. È importante notare che il radicando deve essere non negativo; altrimenti, si potrebbero ottenere contraddizioni come nel caso di [3]√(2) = [6]√(2^2) = [6]√((-2)^(2)) ≠ [3]√(-2).
Riduzione di due radicali allo stesso indice
La riduzione di due radicali allo stesso indice è una tecnica utile per moltiplicare e dividere radicali con indici diversi. Il metodo consiste nei seguenti passaggi:
- Consideriamo due radici con due indici distinti [n]√(a), [m]√(b).
- Calcoliamo il minimo comune multiplo tra n ed m. Esso diventerà l’indice comune a tutte le radici.
- Dividiamo il nuovo indice per i rispettivi indici delle radici e eleviamo i radicandi ai rispettivi quozienti.
In questo modo, otterremo nuove radici equivalenti a quelle date. Ad esempio, per ridurre allo stesso indice i radicali [3]√(8) e [4]√(16), calcoliamo il minimo comune multiplo tra 3 e 4, che è 12, e diventa il nuovo indice delle radici: sqrt[12]…, sqrt[12]…. Dividiamo 12 per 3 e otteniamo 4, che è l’esponente del primo radicando. Dividiamo 12 per 4 e otteniamo 3, che è l’esponente del secondo radicando:
Moltiplicazione e divisione di radicali con indici diversi
Per effettuare il prodotto e il quoziente di radici con indici diversi, è necessario ridurle allo stesso indice, dopodiché si possono utilizzare le proprietà per la moltiplicazione e divisione di radicali con lo stesso indice. Ad esempio:
[3]√(2)×[2]√(3) =
riduciamo i radicali allo stesso indice
= [6]√(2^2)×[6]√(3^3) = [6]√(4)×[6]√(27) =
utilizzando la proprietà dei radicali per la moltiplicazione che abbiamo visto in precedenza
= [6]√(4×27) = [6]√(108)
Potenza di un radicale
La potenza m-esima di una radice che ha indice n e radicando a è una radice che ha per indice n e per radicando la potenza am. Vale la relazione:
([n]√(a))^m = [n]√(a^m) ∀ a ≥ 0, con n,m∈N
Radice di radice
La radice m-esima di una radice n-esima con radicando a è una radice che ha per indice il prodotto degli indici e per radicando a:
[m]√(sqrt[n]a) = sqrt[m×n]a con m,n∈ N
Esempi:
([3]√(3))^(2) = [3]√(3^2) = [3]√(9) ; [3]√(sqrt[4]3) = sqrt[12]3
Fonte: https://www.matematika.it/radicali-e-radici.htm
Trasporto di un fattore dentro il segno di radice
Il trasporto di un fattore al di fuori del segno di radice può essere utile in alcune situazioni matematiche. Si può trasportare il fattore sotto il segno di radice in modo sicuro se il fattore è positivo. In questo caso, si può procedere come segue:
a[n]√(b) = [n]√(a^n·b) con a,b ≥ 0, n∈N
In pratica, quando un radicale è moltiplicato per un fattore positivo, il numero può essere portato dentro la radice dopo averlo elevato ad una potenza uguale all’indice della radice.
Ma cosa succede se il fattore fuori dalla radice è negativo? In questo caso, si può semplicemente trasportare il numero senza il segno all’interno della radice, mentre il meno rimane fuori.
Esempi
- 2[3]√(3) = [3]√(2^3·3) = [3]√(24)
- -5√(7) = -√(5^2·7) = -√(175)
Trasporto di un fattore fuori dal segno di radice
La tecnica del trasporto al di fuori del segno il radice è un metodo che consiste nell’applicare il trasporto dentro al segno di radice al contrario:
[n]√(a^n·b) = a[n]√(b) con a,b ≥ 0, n∈N
Tale ugualglianza permette di trasportare fuori dalla radice un fattore (positivo) del radicando, purché esso sia una potenza con esponente uguale all’indice della radice.
Esempi
√(12) = √(2^2·3) = 2√(3)[4]√(80) = [4]√(2^4·5) = 2[4]√(5)
Più in generale, il trasporto fuori dal segno di radice vale se all’interno del radicando c’è un fattore che sia una potenza con esponente che è un multiplo del radicando, ovvero:
[n]√(a^(nq)·b) = a^q [n]√(b)
Ancora più in generale, ogni fattore all’interno del radicando che abbia un esponente maggiore dell’indice della radice può essere trasportato fuori.
Esempi
[3]√(192) = [3]√(2^6·3) = [3]√(2^(3·2)·3) = 2^2 [3]√(3) = 4[3]√(3)[4]√(160) = [4]√(2^5·5)
L’esponente del 2 è 5 ed è maggiore dell’indice della radice. Per una nota proprietà delle potenze:
2^5 = 2^4·2
quindi abbiamo:
[4]√(160) = [4]√(2^5·5) = [4]√(2^4·2·5) = 2 [4]√(2·5) = 2[4]√(10)
Stai guardando: RADICALI E PROPRIETÀ DEI RADICALI