TRIANGOLO EQUILATERO
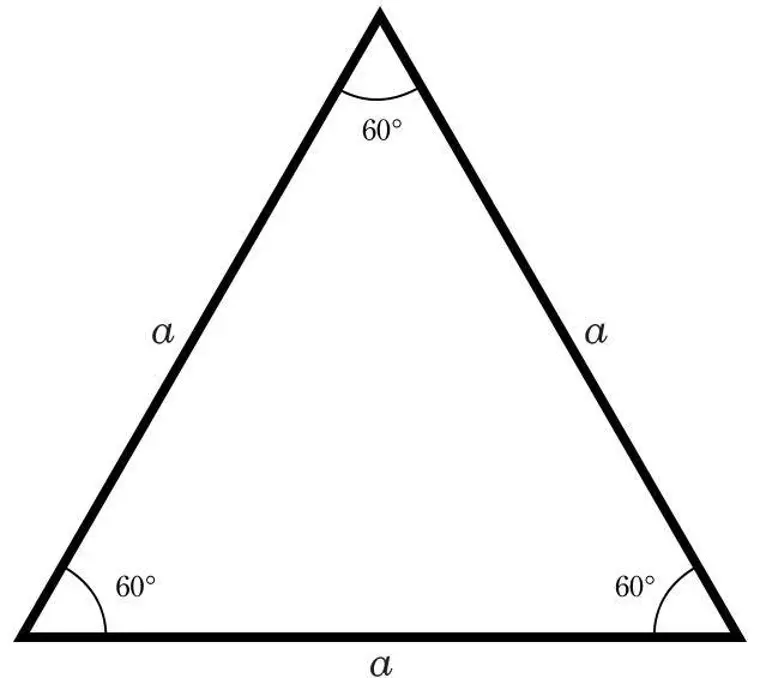
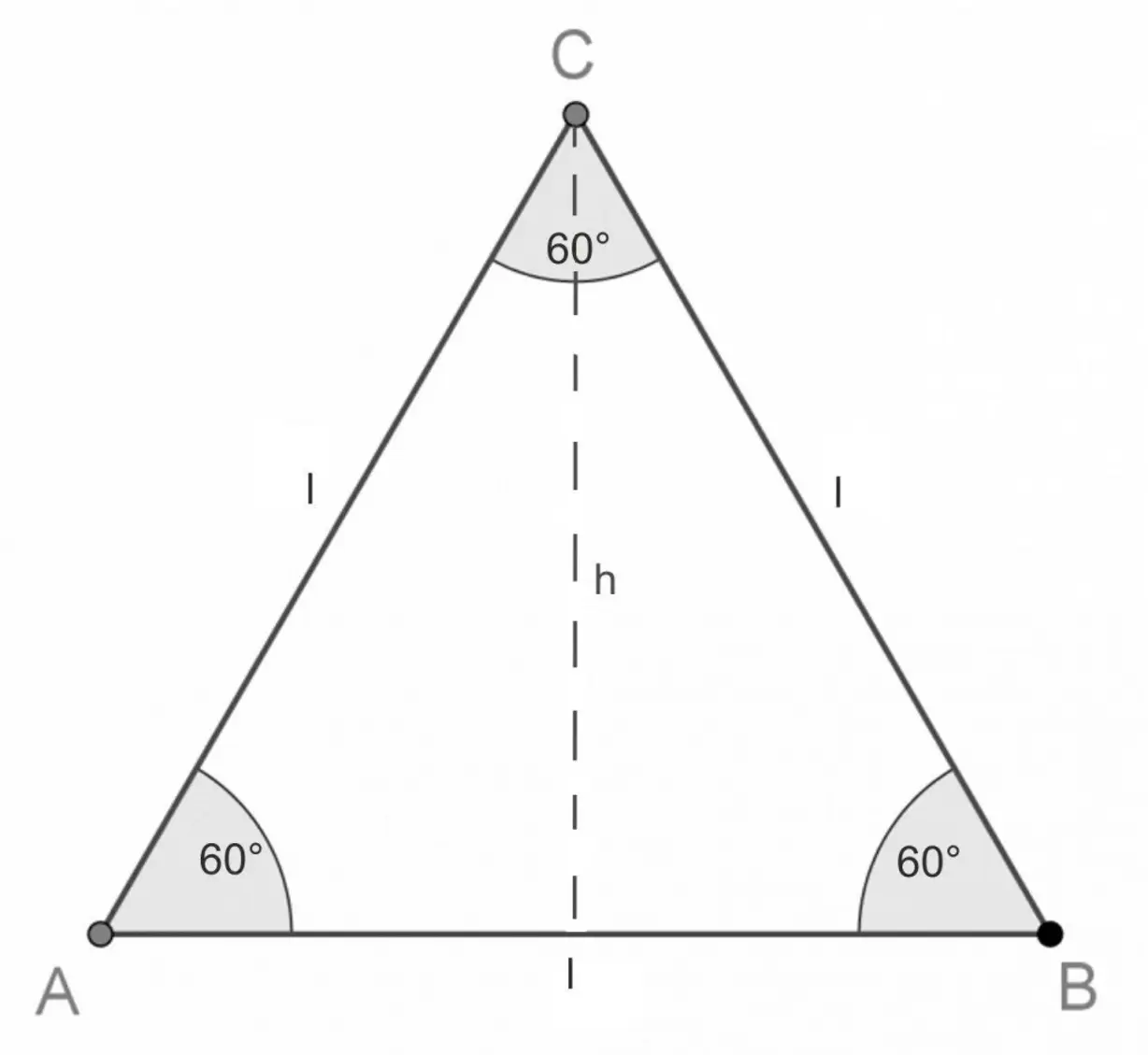
Un triangolo equilatero è un poligono regolare che ha tre lati congruenti, ovvero della stessa lunghezza, e tre angoli interni con ampiezza di 60° ciascuno. Grazie alla sua regolarità, il triangolo equilatero rappresenta il poligono con il minor numero di lati che è possibile costruire.

Nel seguito, abbiamo raccolto tutte le formule del triangolo equilatero, comprese le formule inverse e quelle relative alla circonferenza inscritta e alla circonferenza circoscritta. Queste formule risultano particolarmente utili per risolvere problemi legati a questo tipo di triangolo. In particolare, è possibile utilizzare diverse formule per calcolare l’area del triangolo equilatero.
Definizione del Triangolo Equilatero
Il triangolo equilatero è un tipo di triangolo che presenta tre lati congruenti, ovvero tutti e tre i lati hanno la stessa lunghezza. In altre parole, se si prendono tre segmenti di lunghezza uguale e li si uniscono alle loro estremità, si ottiene un triangolo equilatero.
Triangolo Equilatero ed Equiangolo
Il triangolo equilatero è anche un triangolo equiangolo, poiché presenta tre angoli di uguale ampiezza, ciascuno di 60 gradi. In altre parole, se si disegnano tre raggi che partono dal centro di un cerchio e si uniscono alle estremità della circonferenza, i punti di intersezione dei raggi formano un triangolo equilatero ed equiangolo.
Classificazione dei Triangoli
Il triangolo equilatero rientra sia nella classificazione dei triangoli secondo i lati che in quella secondo gli angoli. Infatti, appartiene alla categoria dei triangoli equilateri e contemporaneamente alla categoria dei triangoli equiangoli.
Fonte del contenuto: https://it.wikipedia.org/wiki/Triangolo_equilatero
Formule del Triangolo Equilatero
Il triangolo equilatero è un tipo di triangolo con tre lati congruenti e tre angoli di uguale ampiezza. Vediamo alcune delle formule utili per risolvere i problemi relativi a questo tipo di figura geometrica.
Triangolo equilatero – YouTube
Significato dei Simboli
Prima di iniziare con le formule del triangolo equilatero, dobbiamo chiarire il significato dei simboli utilizzati.
- L = Lunghezza del lato
- H = Altezza relativa a un lato
- 2p = Perimetro
- S = Area del triangolo equilatero
- r = Apotema (raggio della circonferenza inscritta)
- R = Raggio della circonferenza circoscritta
Formule del Triangolo Equilatero
Nella seguente tabella sono presenti le formule del triangolo equilatero. Le formule evidenziate in grassetto sono quelle da cui, mediante semplici passaggi algebrici ed eventuali sostituzioni, è possibile ricavare tutte le altre formule.
<
Proprietà del Triangolo Equilatero
Il triangolo equilatero è un tipo di triangolo con alcune proprietà particolari. Vediamole nel dettaglio.
Poligono Regolare
Il triangolo equilatero è un poligono regolare. Ciò significa che ha tre lati congruenti e tre angoli di uguale ampiezza (60°). In altre parole, è possibile costruire il triangolo equilatero utilizzando un compasso e una riga, poiché è possibile ottenere tutte le sue parti a partire da una sola.
Il Poligono Regolare con il Minor Numero di Lati
Il triangolo equilatero è il poligono regolare con il minor numero di lati che si possa costruire.
Bisettrici, Median, Altezze e Assi Coincidono
Le bisettrici, le mediane, le altezze e gli assi del triangolo equilatero coincidono. Ciò significa che il punto di intersezione delle bisettrici, delle mediane e delle altezze coincide con il baricentro, l’ortocentro, l’incentro e il circocentro del triangolo.

Assi di Simmetria
Il triangolo equilatero ha tre assi di simmetria: ciascuna delle tre altezze è un asse di simmetria per il triangolo equilatero.
Triangolo Acutangolo e Isoscele
Il triangolo equilatero è un particolare tipo di triangolo acutangolo, in quanto ha tre angoli acuti. Inoltre, è anche un particolare tipo di triangolo isoscele, poiché ha anche due angoli di uguale ampiezza.
| Grandezza | Formula |
|---|---|
| Perimetro | 2p = 3L |
| Lato | L = (2p)/(3) |
| Altezza (teorema di Pitagora) | H = (L√(3))/(2) |
| Lato (dall’altezza) | L = (2H)/(√(3)) |
| Perimetro (con l’altezza) | 2p = 2H√(3) |
| Altezza (dal perimetro) | H = (2p)/(2√(3)) |
| Area | S = (H×L)/(2) |
| Area (solo con il lato) | S = (√(3))/(4)L^2 |
| Area (solo con l’altezza) | S = (H^2)/(√(3)) |
| Apotema (con il lato) | r = (1)/(2√(3))L |
| Apotema (con l’altezza) | r = (1)/(3)H |
Stai guardando: TRIANGOLO EQUILATERO