TRIANGOLO ISOSCELE
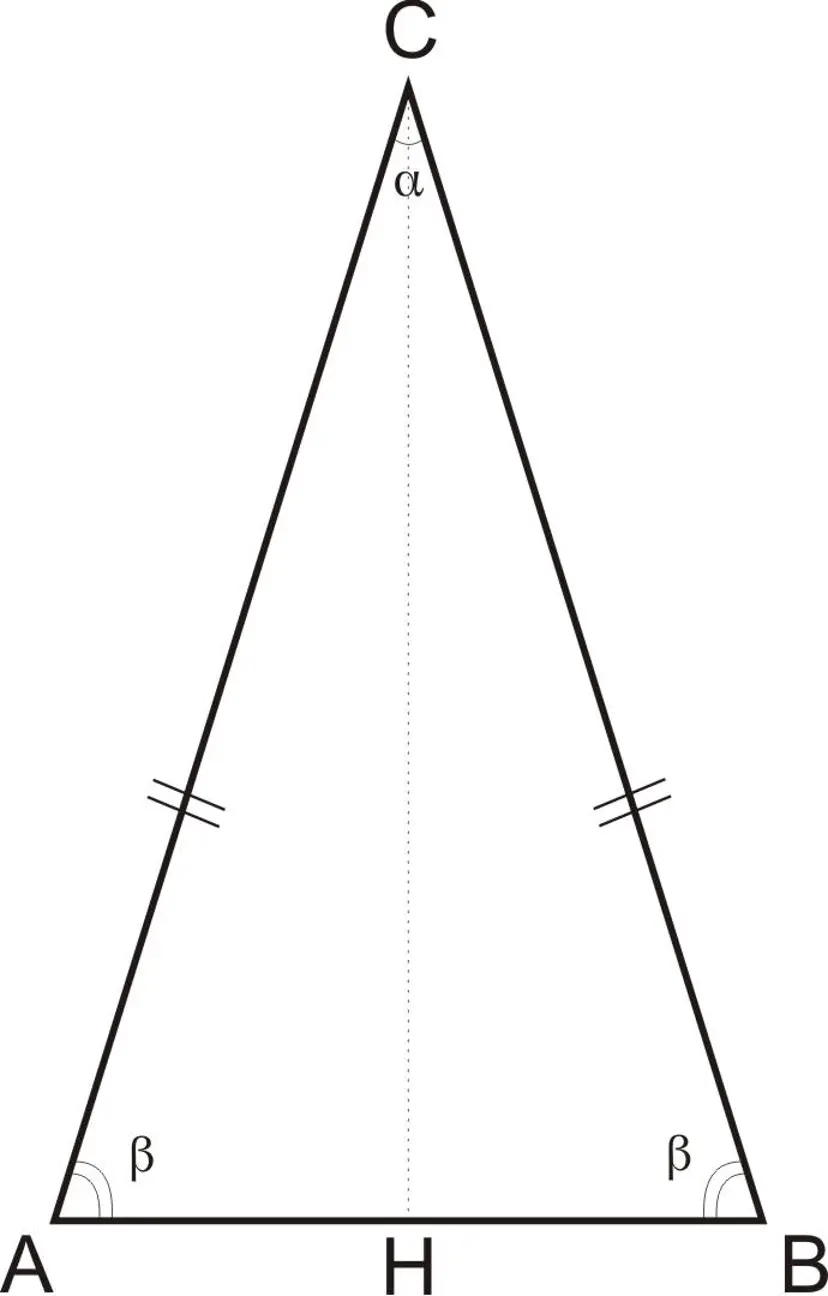
Un triangolo isoscele è un tipo di triangolo in cui due lati sono congruenti e quindi anche gli angoli opposti a questi lati sono congruenti. Il terzo lato, che non è congruente agli altri due, viene chiamato base del triangolo. L’altezza del triangolo isoscele è la distanza tra la base e il vertice opposto alla base. In questa lezione, oltre a definire il triangolo isoscele, esamineremo tutte le formule utili per calcolare la sua area e la sua altezza, sia in forma diretta che inversa, consentendo di risolvere qualsiasi problema di geometria riguardante i triangoli isosceli.

Inoltre, elencheremo le proprietà dei triangoli isosceli, concentrandoci in particolare sugli angoli e le altezze. Infine, forniremo una vasta raccolta di esercizi e problemi svolti che aiuteranno a consolidare la comprensione dei concetti presentati. È importante notare che, nel caso particolare del triangolo rettangolo isoscele, verrà trattato un approfondimento specifico, tuttavia le formule e le proprietà elencate per i triangoli isosceli valgono anche per questo caso particolare.
Definizione di triangolo isoscele
Un triangolo isoscele è un tipo di triangolo che ha due lati congruenti. Questo significa che i due lati hanno la stessa lunghezza, mentre il terzo lato può essere di lunghezza diversa. In altre parole, un triangolo isoscele è caratterizzato dalla sua simmetria rispetto alla linea che congiunge i vertici corrispondenti ai lati congruenti.
Equivalenza tra lati e angoli
Inoltre, possiamo affermare che un triangolo isoscele ha anche due angoli di uguale ampiezza. Questo è un’altra proprietà che deriva dalla congruenza dei lati. Se due lati di un triangolo sono congruenti, i due angoli che si oppongono a questi lati sono necessariamente congruenti. Pertanto, un triangolo isoscele può essere definito anche in base alla sua simmetria rispetto all’asse che congiunge i due angoli corrispondenti ai lati congruenti.
Classificazione dei triangoli
Vale la pena sottolineare che la classificazione dei triangoli in base ai lati e agli angoli è importante per la geometria e per la risoluzione di problemi matematici. Nel caso dei triangoli isosceli, la classificazione in base ai lati è preferibile poiché rende più facile riconoscere e risolvere i problemi legati alla simmetria e alla congruenza dei lati.
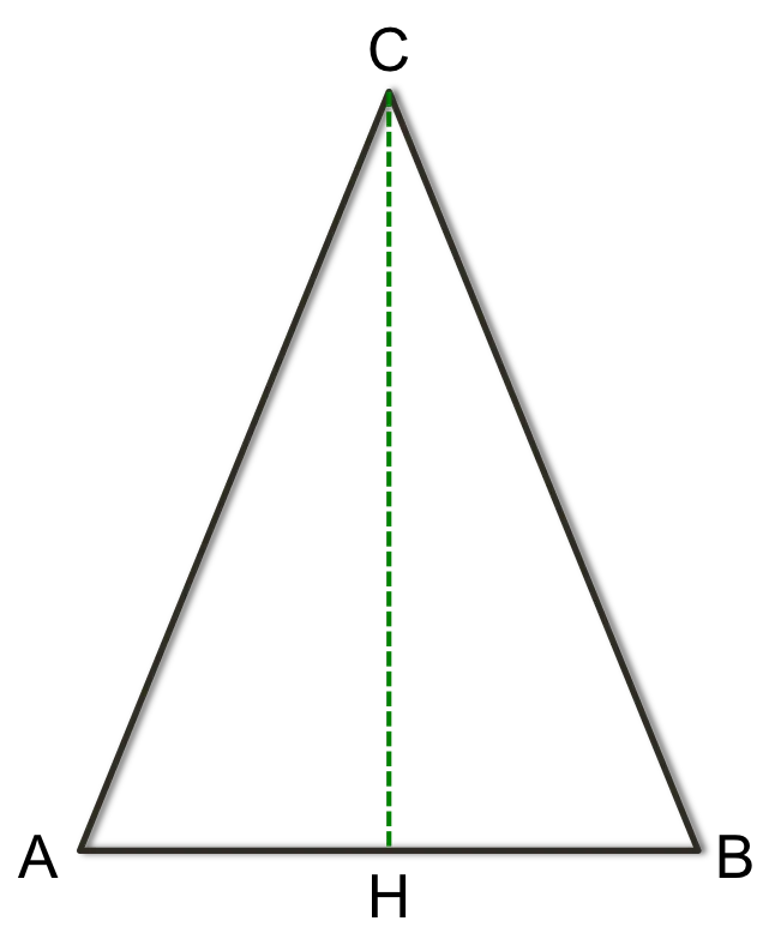
Fonte:
Adattato da: Math Planet
Il teorema del triangolo isoscele – dimostrazione – YouTube
Formule del triangolo isoscele
Il triangolo isoscele è un tipo di triangolo con due lati congruenti e uno diverso, chiamato base. Esistono diverse formule matematiche per calcolare le sue proprietà, come il perimetro, l’area e le altezze relative ai lati. Di seguito riportiamo le formule principali del triangolo isoscele.
Simboli utilizzati
Prima di elencare le formule, è importante comprendere il significato dei simboli utilizzati. In particolare:
- b: base del triangolo
- L: lato obliquo congruente
- H: altezza relativa alla base b
- h: altezza relativa al lato obliquo L
- 2p: perimetro del triangolo
- S: area del triangolo
Formule principali
Nella seguente tabella sono elencate le formule principali del triangolo isoscele, evidenziate in grassetto, da cui è possibile ricavare le altre formule inverse e dirette.
| Proprietà | Formula |
|---|---|
| Perimetro | 2p = 2L + b |
| Lato obliquo (dal perimetro) | L = (2p – b) / 2 |
| Base (dal perimetro) | b = 2p – 2L |
| Area | S = (b x H) / 2 |
| Altezza relativa alla base | H = (2S) / b |
| Base (dall’area) | b = (2S) / H |
| Area | S = (L x h) / 2 |
| Altezza relativa al lato obliquo | h = (2S) / L |
| Lato obliquo (dall’area) | L = (2S) / h |
| Lato obliquo (teorema di Pitagora) | L = √(H2 + (b2 / 4)) |
| Altezza relativa alla base | H = √(L2 – ( Proprietà del triangolo isoscele Il triangolo isoscele è un tipo di triangolo che presenta alcune proprietà particolari. Proprietà principali Le proprietà principali del triangolo isoscele sono: I lati obliqui sono congruenti, cioè hanno la stessa lunghezza. Gli angoli alla base sono congruenti, cioè hanno la stessa misura. Un triangolo isoscele è simmetrico rispetto all’altezza relativa alla base. Questo significa che se tracciamo l’altezza del triangolo relativa alla base, essa divide il triangolo in due parti simmetriche. Le altezze relative ai lati obliqui sono congruenti, cioè hanno la stessa lunghezza. L’altezza relativa alla base divide il triangolo in due triangoli rettangoli congruenti. In altre parole, se tracciamo l’altezza relativa alla base, essa forma con la base stessa due segmenti congruenti, ciascuno dei quali forma con un lato obliquo un angolo retto. L’altezza relativa alla base è anche mediana e asse relativo alla base, e bisettrice dell’angolo al vertice. Questo significa che l’altezza relativa alla base ha diverse proprietà interessanti, tra cui quella di dividere la base in due segmenti congruenti, quella di passare per il vertice opposto alla base e quella di dividere l’angolo al vertice in due parti congruenti. Casi particolari Un ulteriore caso particolare è dato dal triangolo rettangolo isoscele, che è un triangolo sia isoscele che rettangolo. In questo caso, essendo un triangolo rettangolo, uno degli angoli misura 90°, mentre gli altri due angoli sono congruenti e misurano 45°. |
Stai guardando: TRIANGOLO ISOSCELE