SENO E COSENO
Il seno e il coseno, rappresentati rispettivamente con sin(α) e cos(α), sono funzioni trigonometriche fondamentali, che vengono definite a partire dalla circonferenza goniometrica e che assegnano ad ogni angolo un valore numerico compreso tra -1 e +1. Lo studio delle funzioni goniometriche costituisce uno dei primi obiettivi della Trigonometria.

In questa lezione, spiegheremo la definizione di seno e coseno di un angolo, con un’attenzione particolare agli aspetti grafici e geometrici. Inoltre, evidenzieremo le proprietà principali delle definizioni di seno e coseno e proporrò diversi esempi. Inoltre, ci riferiremo ad altri approfondimenti utili per coloro che desiderano un ripasso veloce del tema.
Rappresentazione e definizione di seno e coseno
In geometria, il seno e il coseno sono funzioni trigonometriche utilizzate per calcolare la relazione tra gli angoli e i lati di un triangolo rettangolo. Queste funzioni sono ampiamente utilizzate in diverse aree della matematica, come l’algebra, la geometria analitica, la trigonometria e la fisica.
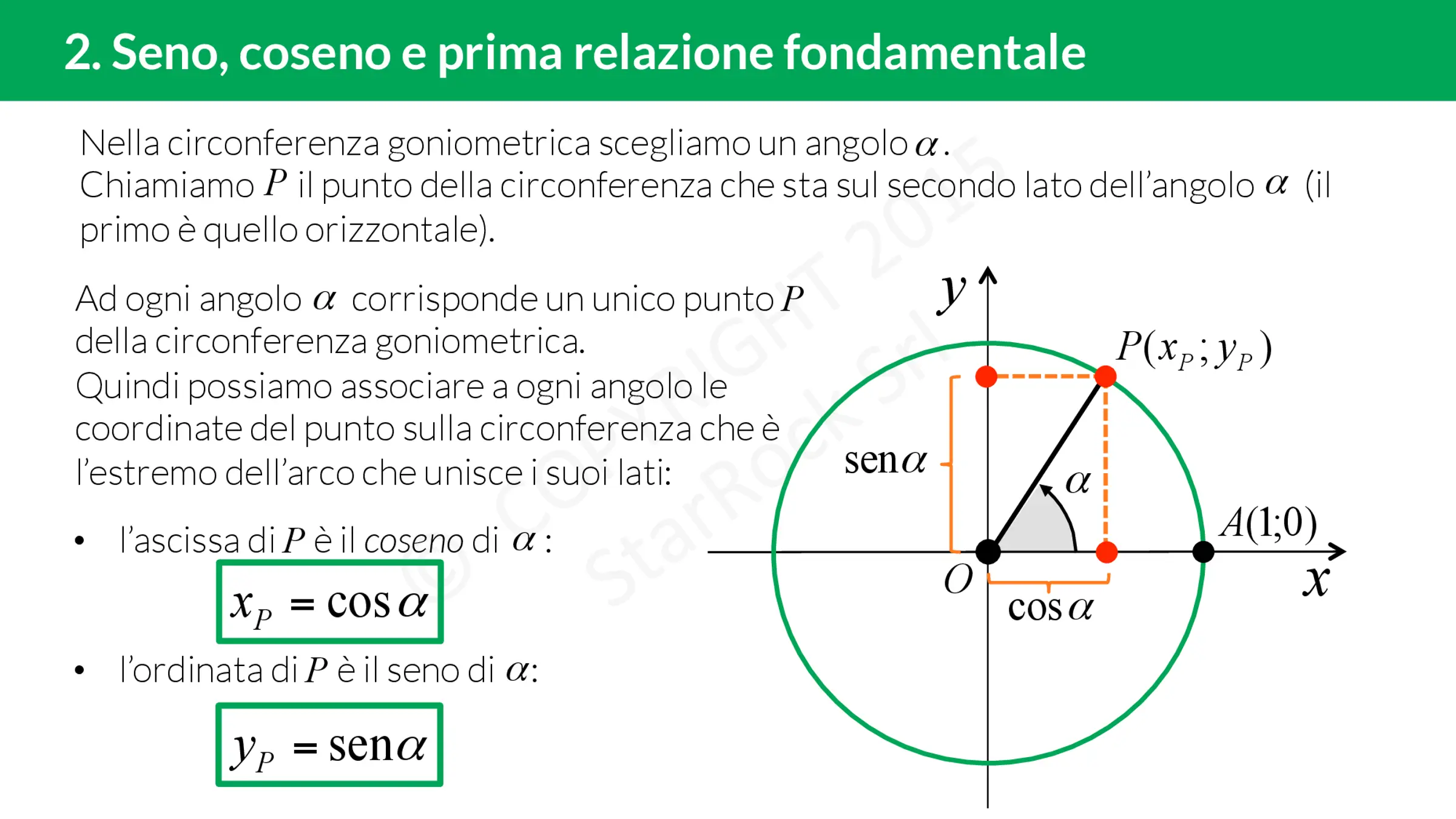
Definizione di seno di un angolo
Dato un angolo α sulla circonferenza goniometrica, il seno dell’angolo α è definito come l’ordinata del punto P associato ad α. In altre parole, il seno di un angolo è il rapporto tra il lato opposto e l’ipotenusa di un triangolo rettangolo che ha come angolo α.
La formula matematica per il seno di un angolo è:
sin(α) = yP/OP
dove yP è l’ordinata del punto P e OP è l’ipotenusa del triangolo rettangolo.
Definizione di coseno di un angolo
Dato un angolo α sulla circonferenza goniometrica, il coseno dell’angolo α è definito come l’ascissa del punto P associato ad α. In altre parole, il coseno di un angolo è il rapporto tra il lato adiacente e l’ipotenusa di un triangolo rettangolo che ha come angolo α.
La formula matematica per il coseno di un angolo è:
cos(α) = xP/OP
dove xP è l’ascissa del punto P e OP è l’ipotenusa del triangolo rettangolo.
Nota bene: sia il seno che il coseno di un angolo sono funzioni periodiche, con un periodo di 360° o 2π radianti.
Seno, Coseno e Tangente : funzioni goniometriche 😉 – YouTube
Esempi su seno e coseno
Di seguito vediamo alcuni esempi di applicazione delle definizioni di seno e coseno e calcoliamo i valori di seno e coseno in corrispondenza di alcuni angoli particolari.
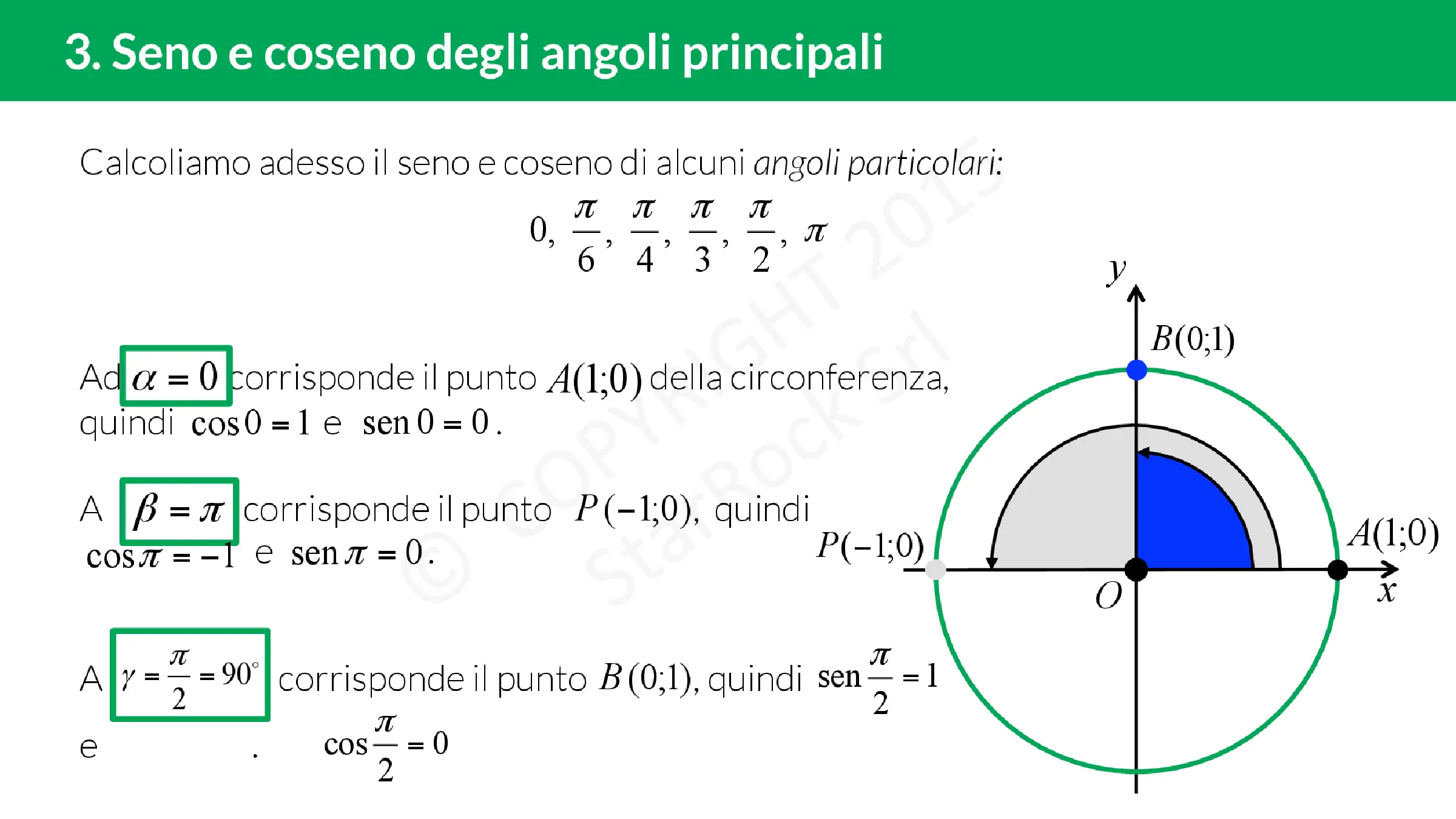
Valori di seno e coseno per angoli particolari
Per calcolare il seno e il coseno di un angolo, fissiamo l’angolo sulla circonferenza goniometrica e applichiamo le definizioni date in precedenza:
- Il seno di un angolo è l’ordinata del punto associato all’angolo o la misura con segno della proiezione sull’asse y del secondo lato dell’angolo;
- Il coseno di un angolo è l’ascissa del punto associato all’angolo o la misura con segno della proiezione del secondo lato dell’angolo sull’asse x.
Ecco alcuni valori di seno e coseno per angoli particolari:
- Se α=0, allora sin(0) = 0 e cos(0) = 1;
- Se α=π/2, allora sin(π/2) = 1 e cos(π/2) = 0;
- Se α=π, allora sin(π) = 0 e cos(π) = -1;
- Se α=3π/2, allora sin(3π/2) = -1 e cos(3π/2) = 0;
- Se α=2π, allora sin(2π) = 0 e cos(2π) = 1.
Inoltre, ci sono tre angoli particolarmente importanti che capitano spesso negli esercizi:
- α = π/6 (30°): sin(π/6) = 1/2 e cos(π/6) = √3/2;
- α = π/4 (45°): sin(π/4) = cos(π/4) = √2/2;
- α = π/3 (60°): sin(π/3) = √3/2 e cos(π/3) = 1/2.
Si noti che per α=π/6 e α=π/3 i valori di seno e coseno sono esattamente invertiti.
Le funzioni seno e coseno
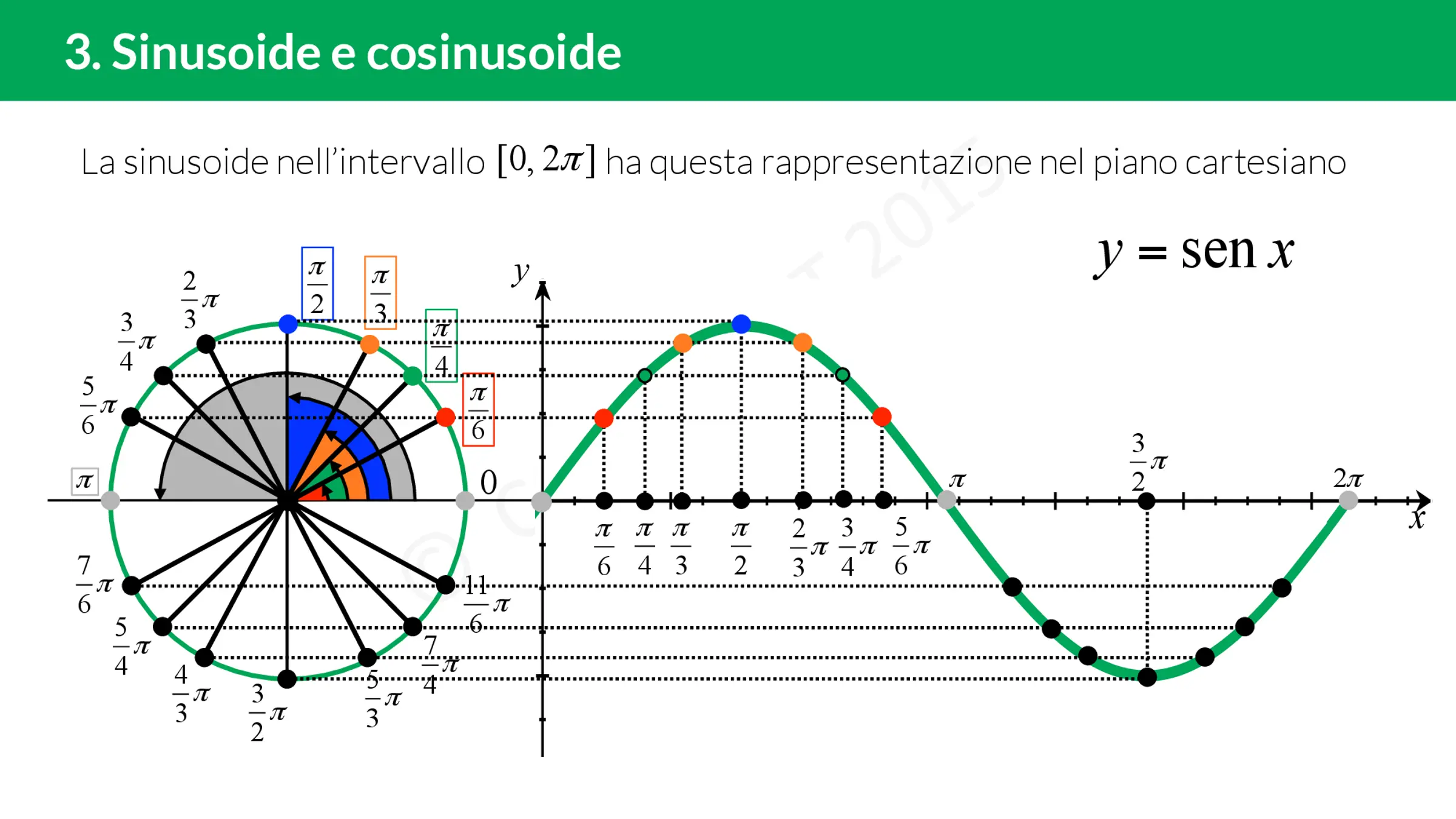
Le funzioni seno e coseno possono essere rappresentate analiticamente mediante un grafico. Ecco alcune informazioni importanti:
Periodicità
I valori di seno e coseno si ripetono se continuiamo a girare sulla circonferenza goniometrica. Pertanto, le due funzioni sono periodiche di periodo 2π:
- sin(α) = sin(α+2kπ) per qualsiasi k∈Z;
- cos(α) = cos(α+2kπ) per qualsiasi k∈Z,
dove k∈Z indica un qualsiasi intero relativo.
Intervallo di valori
I valori di seno e coseno sono sempre compresi tra -1 e 1:
- -1 ≤ sin(x) ≤ +1;
- -1 ≤ cos(x) ≤ +1.
Inoltre, le due funzioni assumono tutti i valori compresi tra -1 e 1:
- ∀ y∈ [-1,1] ∃ x∈ [0,2π) tale che y = sin(x);
- ∀ y∈ [-1,1] ∃ x∈ [0,2π) tale che y = cos(x).
In breve, l’immagine delle funzioni seno e coseno è l’intervallo [-1,1] dei numeri reali.
Fonte: youmath.it
Stai guardando: SENO E COSENO