PIANO CARTESIANO
ente disequazioni.Il piano cartesiano è un sistema di riferimento utilizzato nella Geometria Analitica del piano. È composto da due assi, l’asse x e l’asse y, che si intersecano in un punto detto origine O. Ogni punto del piano viene rappresentato da una coppia ordinata di numeri reali (x,y), dove x rappresenta la coordinata lungo l’asse x, chiamata anche ascissa, e y rappresenta la coordinata lungo l’asse y, chiamata anche ordinata.

Utilizzando le coordinate cartesiane, possiamo rappresentare qualsiasi figura geometrica piana, come punti, rette e curve. La rappresentazione grafica della figura corrisponde alla sua rappresentazione analitica, ovvero la descrizione del luogo mediante numeri, variabili, equazioni ed eventualmente disequazioni. Grazie al piano cartesiano, possiamo quindi disegnare e descrivere qualsiasi figura o ente geometrico piano in modo preciso e coerente.
Cos’è il piano cartesiano e come si rappresenta
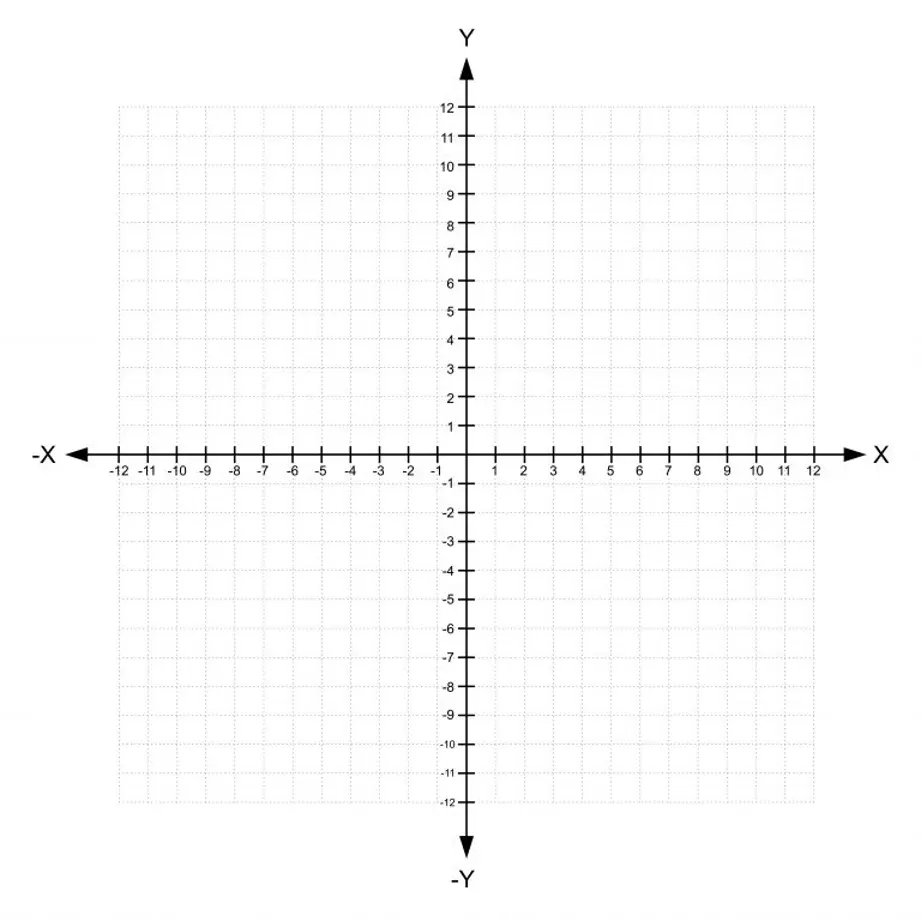
Il piano cartesiano è uno strumento matematico che permette di rappresentare le coordinate di un punto nello spazio bidimensionale. Esso è costituito da due rette perpendicolari tra loro, chiamate assi cartesiani, che dividono il piano in quattro parti uguali chiamate quadranti. L’origine degli assi è il punto di intersezione tra l’asse delle ascisse (orizzontale) e l’asse delle ordinate (verticale).
Disegno del piano cartesiano
Per disegnare il piano cartesiano, basta tracciare due rette perpendicolari tra loro, una orizzontale e una verticale, in modo che si incontrino in un punto comune, l’origine degli assi. L’asse delle ascisse viene solitamente indicato con la lettera x e l’asse delle ordinate con la lettera y. Le coordinate di un punto P nel piano cartesiano si rappresentano con un paio ordinato di numeri (x, y), dove x è la coordinata sull’asse delle ascisse e y è la coordinata sull’asse delle ordinate.
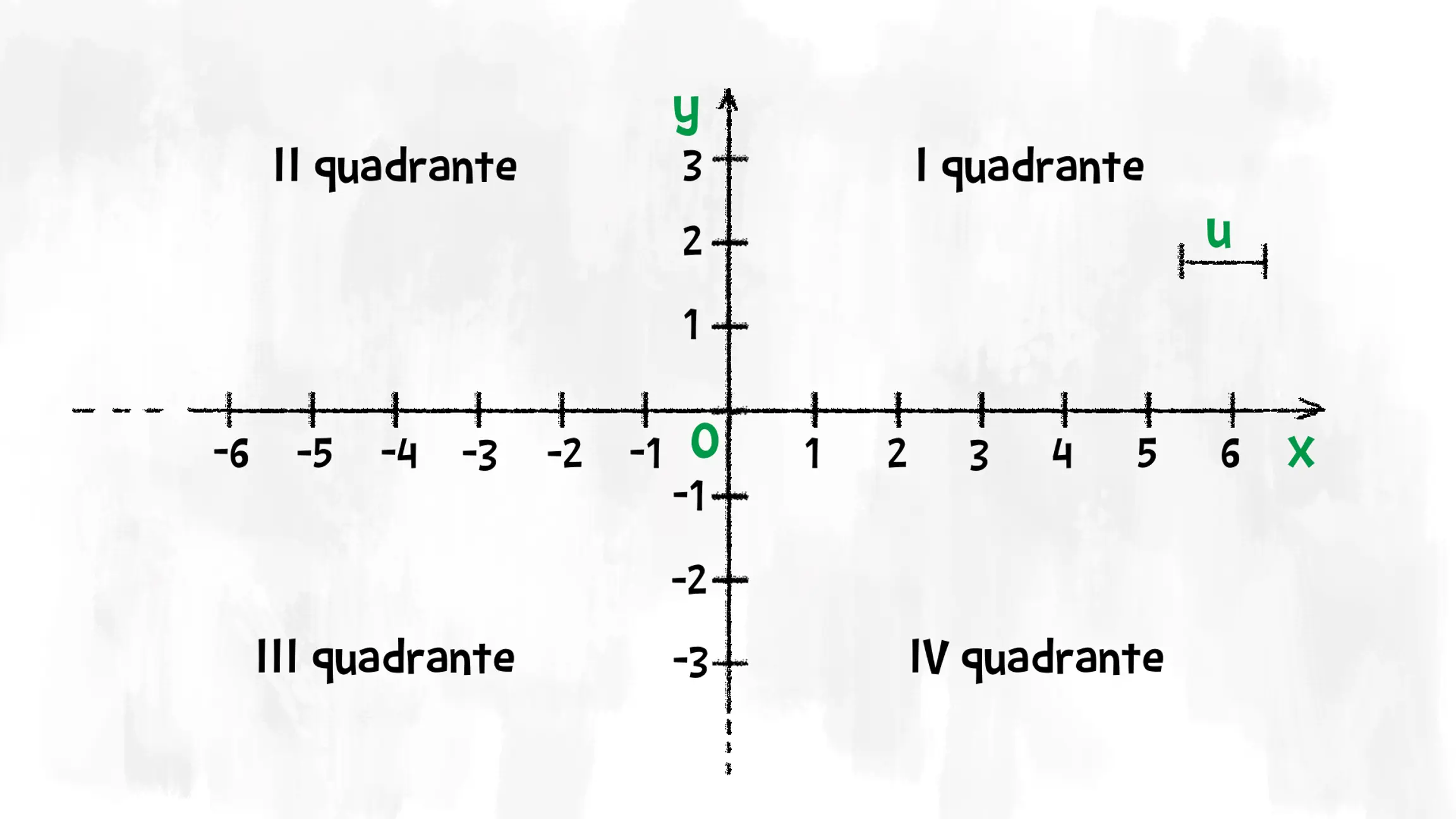
I quadranti del piano cartesiano
Il primo quadrante del piano cartesiano si trova nella parte superiore destra e le coordinate dei suoi punti sono positive sia per l’asse delle ascisse che per l’asse delle ordinate. Nel secondo quadrante, le coordinate sull’asse delle ascisse sono negative, mentre quelle sull’asse delle ordinate sono positive. Nel terzo quadrante, invece, entrambe le coordinate sono negative, mentre nel quarto quadrante le coordinate sull’asse delle ascisse sono positive e quelle sull’asse delle ordinate sono negative.
Fonte del contenuto:
Fonte del contenuto: math.it
PIANO CARTESIANO 1 introduzione _ PC05 – YouTube
Piano cartesiano e sistema di coordinate
Il piano cartesiano è uno strumento matematico che consente di costruire un sistema di coordinate, fondamentale per la rappresentazione di figure geometriche piane. Il sistema di coordinate è costituito da due assi orientati: l’asse delle ascisse (o x) e l’asse delle ordinate (o y), che sono orientati rispettivamente da sinistra a destra e dal basso verso l’alto.
Rappresentazione dei numeri reali nel piano cartesiano
Ciascuno dei due assi viene utilizzato per rappresentare l’insieme dei numeri reali R, ovvero l’insieme di tutti i numeri decimali, razionali e irrazionali. Si utilizza un’unità di misura di riferimento, solitamente rappresentata da un quadretto, che corrisponde ad un’unità intera, ovvero 1. L’origine degli assi, il punto di intersezione tra le due rette, viene assegnato il valore di x=0 sull’asse delle ascisse e y=0 sull’asse delle ordinate.
Coordinate cartesiane e rappresentazione dei punti nel piano cartesiano
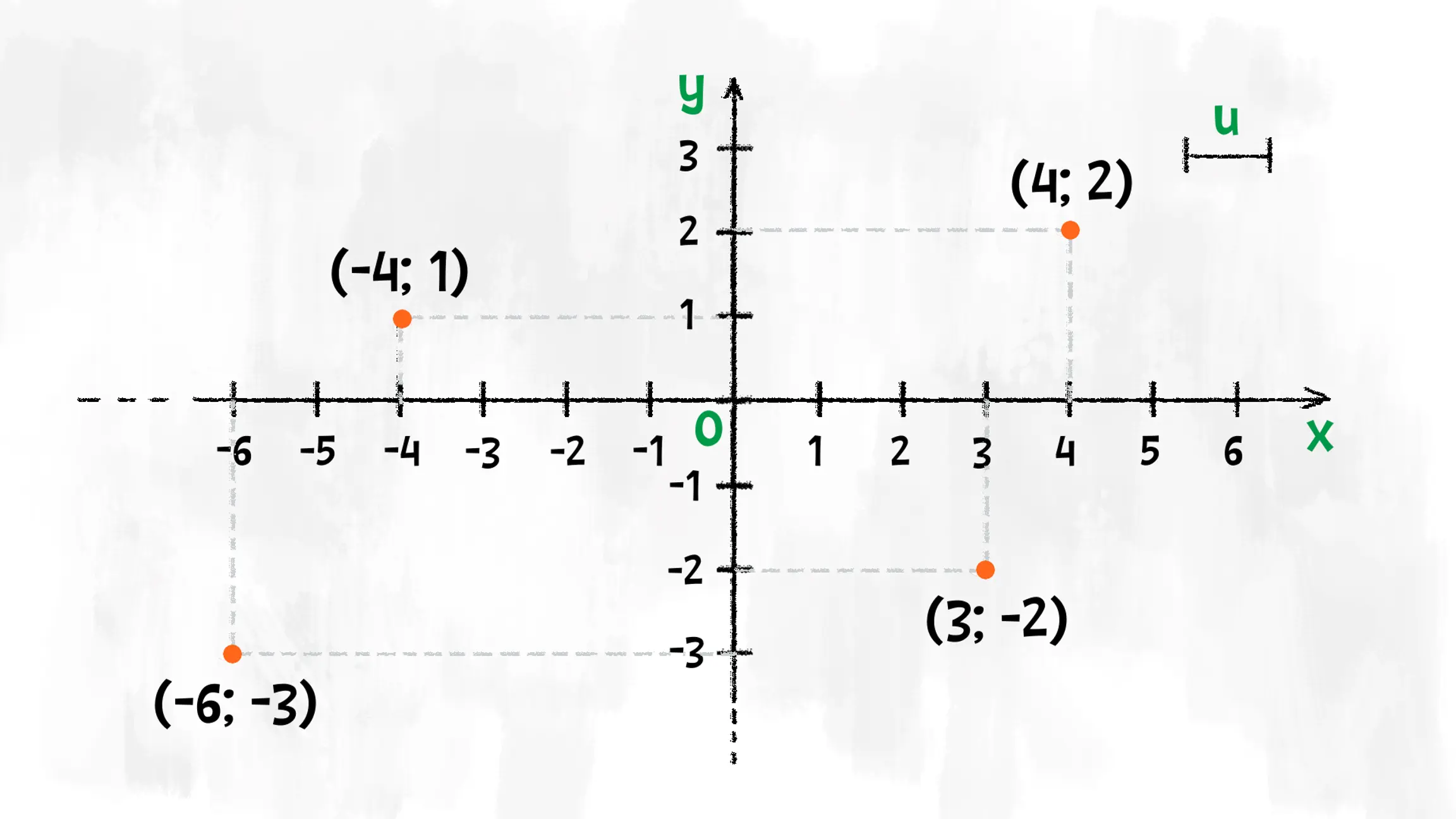
Un qualsiasi punto del piano cartesiano può essere rappresentato mediante una coppia ordinata di numeri reali, cioè le coordinate cartesiane (x, y) del punto. In particolare, l’ascissa x si riferisce all’asse delle ascisse (orizzontale) e l’ordinata y si riferisce all’asse delle ordinate (verticale). Per individuare l’ascissa del punto si considera la proiezione ortogonale del punto sull’asse delle x e per trovare l’ordinata del punto si proietta il punto stesso perpendicolarmente sull’asse delle y.
Corrispondenza biunivoca
In questo modo, abbiamo una corrispondenza biunivoca tra le coppie di valori e i punti del piano, cioè ad ogni punto del piano corrisponde una e una sola coppia di numeri reali e ad una qualsiasi coppia di numeri reali corrisponde uno ed un solo punto del piano.
Fonte del contenuto:
Fonte del contenuto: damtp.cam.ac.uk
Esempio di rappresentazione nel piano cartesiano
Vediamo un esempio di rappresentazione nel piano cartesiano. Dobbiamo rappresentare il triangolo di vertici:
P1 = (3,3), P2 = (3,0), P3 = (0,3).
Rappresentazione del triangolo nel piano cartesiano
Per rappresentare il triangolo nel piano cartesiano Oxy, disegniamo gli assi cartesiani Oxy, utilizzando un’unità di misura di riferimento e graduando gli assi. Successivamente, segniamo i punti P1, P2, P3 sul piano cartesiano. Il punto P1 ha coordinate (3,3), quindi si trova a 3 unità sia sull’asse delle x che sull’asse delle y. Il punto P2 ha coordinate (3,0), quindi si trova a 3 unità sull’asse delle x e sulla stessa linea dell’asse delle y. Infine, il punto P3 ha coordinate (0,3), quindi si trova sulla stessa linea dell’asse delle x e a 3 unità sull’asse delle y.
Rappresentazione del triangolo nel piano cartesiano
Il triangolo è formato dai punti P1, P2, P3 collegati tra loro da segmenti di retta. La figura ottenuta rappresenta il triangolo nel piano cartesiano.
Stai guardando: PIANO CARTESIANO