ALTEZZA TRIANGOLO RETTANGOLO
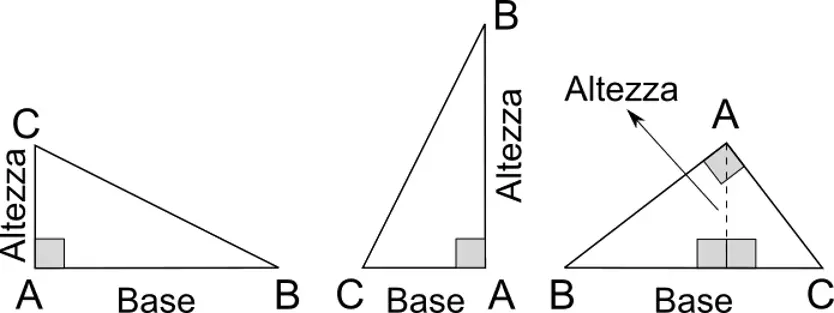
L’altezza di un triangolo rettangolo è definita come la lunghezza del segmento perpendicolare all’ipotenusa che parte dal vertice dell’angolo retto. Per calcolarla, si può utilizzare la formula h=c1·c2/i, dove c1 e c2 rappresentano i due cateti del triangolo e i è la lunghezza dell’ipotenusa. In pratica, per trovare l’altezza, si moltiplicano tra loro i due cateti e si divide il risultato per l’ipotenusa. Questo calcolo è importante in molte applicazioni geometriche e matematiche.

Altezze del triangolo rettangolo e altezza relativa all’ipotenusa
Il triangolo rettangolo ha tre altezze, tanti quanti sono i suoi vertici. Tuttavia, le altre due altezze coincidono con i due cateti, che sono l’uno l’altezza relativa all’altro. Quindi, quando si parla di altezza del triangolo rettangolo, ci si riferisce implicitamente all’altezza relativa all’ipotenusa.
Formule per l’altezza del triangolo rettangolo
Nella seguente tabella sono riportate le formule per l’altezza del triangolo rettangolo:
| Tipo di formula | Formula per l’altezza del triangolo rettangolo |
|---|---|
| Altezza triangolo rettangolo con area e ipotenusa | h = (2S)/(i) |
| Altezza triangolo rettangolo con cateti e ipotenusa | h = (c1×c2)/(i) |
| Altezza triangolo rettangolo con cateto minore e sua proiezione sull’ipotenusa | h = √(c12-p12) |
| Altezza triangolo rettangolo con cateto maggiore e sua proiezione sull’ipotenusa | h = √(c22-p22) |
| Altezza triangolo rettangolo con proiezioni dei cateti sull’ipotenusa | h = √(p1×p2) |
Esercizi svolti sull’altezza del triangolo rettangolo
Qui di seguito sono presentati alcuni esercizi svolti sull’altezza del triangolo rettangolo, in cui sono state utilizzate le varie formule e mostrati esempi di applicazione.
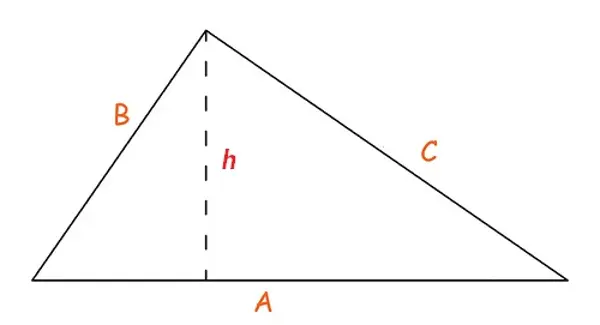
Calcolo altezza triangolo rettangolo con area e ipotenusa
L’area di un triangolo rettangolo si calcola moltiplicando tra loro le misure di ipotenusa e altezza, e dividendo il risultato per 2:
S = (i×h)/(2)
Invertendo la precedente relazione in favore di h si ottiene la formula diretta che permette di calcolare la misura dell’altezza conoscendo l’area e la misura dell’ipotenusa:
h = (2S)/(i)
Esempio:
Determinare la misura dell’altezza di un triangolo rettangolo sapendo che la sua area è di 9,5 metri quadrati e che l’ipotenusa misura 5 metri.
h = (2S)/(i) = (2×(9,5 m^2))/(5 m) = (19 m^2)/(5 m) = 3,8 m
Altezza relativa all’ipotenusa: come calcolarla – Seconda Media [Tutorial per genitori] – YouTube
Calcolo altezza triangolo rettangolo con cateti e ipotenusa
Se si conoscono le misure dei tre lati di un triangolo rettangolo si può trovare l’altezza moltiplicando le misure dei due cateti e dividendo il risultato per la lunghezza dell’ipotenusa:
h = (c1×c2)/(i)
Esempio:
Il perimetro di un triangolo rettangolo è di 12 centimetri e i due cateti misurano 3 cm e 4 cm. Calcolare la misura dell’altezza.
Dalla formula per il perimetro del triangolo rettangolo
2p = c1+c2+i
si può ricavare la misura dell’ipotenusa
i = 2p-c1-c2 = 12 cm-3 cm-4 cm = 5 cm
per poi calcolare l’altezza
h = (c1×c2)/(i) = ((3 cm)×(4 cm))/(5 cm) = (12 cm^2)/(5 cm) = 2,4 cm
Fonte: skuola.net
Calcolo altezza triangolo rettangolo con cateto e sua proiezione sull’ipotenusa
Per determinare l’altezza si può estrarre la radice quadrata della differenza tra il quadrato della misura di un cateto e il quadrato della misura della sua proiezione sull’ipotenusa:
h = √(c12-p12) ; h = √(c22-p22)
Le precedenti formule discendono dal teorema di Pitagora, infatti l’altezza relativa all’ipotenusa divide il triangolo in due nuovi triangoli rettangoli, aventi:
- come ipotenusa uno dei due cateti del triangolo di partenza;
- come cateti, l’altezza e la proiezione di ciascun cateto sull’ipotenusa.
Esempio:
Il cateto minore di un triangolo rettangolo e la sua proiezione sull’ipotenusa misurano, rispettivamente, 17 dm e 8 dm. Determinare la misura dell’altezza.
h = √(c12-p12) = √((17 dm)2-(8 dm)2) = √(289 dm2-64 dm2) = √(225 dm2) = 15 dm
Calcolo altezza triangolo rettangolo con le proiezioni dei due cateti sull’ipotenusa
Dal secondo teorema di Euclide sappiamo che l’altezza relativa all’ipotenusa è il medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa:
p1:h = h:p2
Applicando la proprietà fondamentale delle proporzioni otteniamo la formula:
h^2 = p1×p2
e quindi possiamo ricavare la misura dell’altezza estraendo la radice quadrata del prodotto tra le proiezioni dei cateti:
h = √(p1×p2)
Esempio:
Calcolare la misura dell’altezza di un triangolo rettangolo in cui le proiezioni dei due cateti sull’ipotenusa sono di 25 cm e 9 cm.
h = √(p1×p2) = √((25 cm)×(9 cm)) = √(225 cm2) = 15 cm
Fonte: Wikipedia
Stai guardando: ALTEZZA TRIANGOLO RETTANGOLO