IPOTENUSA DEL TRIANGOLO RETTANGOLO: DEFINIZIONE, FORMULE ED ESEMPI

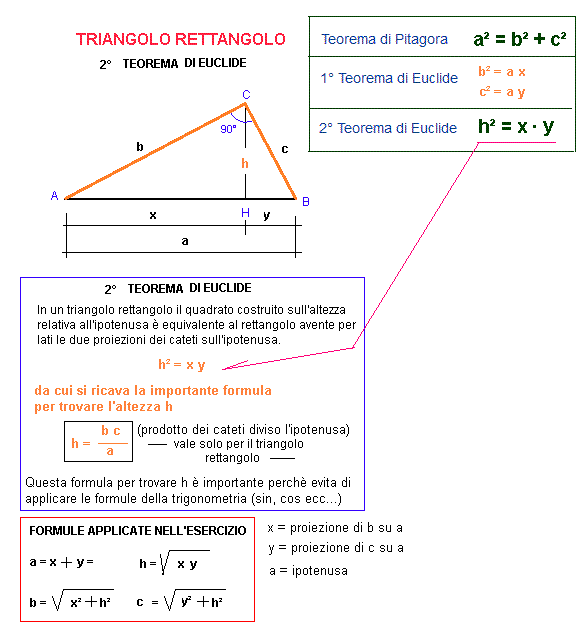
L’ipotenusa di un triangolo rettangolo è il lato più lungo che si trova di fronte all’angolo retto. La sua lunghezza può essere calcolata utilizzando il teorema di Pitagora, che afferma che l’ipotenusa al quadrato è uguale alla somma dei quadrati dei cateti.

Pertanto, l’ipotenusa può essere espressa come i=√(c1²+c2²), dove c1 e c2 sono le lunghezze dei cateti. Tuttavia, ci sono anche altre formule e metodi per calcolare l’ipotenusa, a seconda dei dati di cui si dispone.

Formule per l’ipotenusa del triangolo rettangolo

Il triangolo rettangolo è un tipo di triangolo che possiede un angolo retto, ovvero un angolo di 90°. In questo tipo di triangolo, l’ipotenusa è il lato opposto all’angolo retto e costituisce il lato più lungo del triangolo.

Formule dirette per il calcolo dell’ipotenusa del triangolo rettangolo:

Abbiamo diverse formule per il calcolo dell’ipotenusa di un triangolo rettangolo:

Ipotenusa del triangolo rettangolo con i due cateti

La formula diretta più comune per il calcolo dell’ipotenusa è:

i = √(c₁²+c₂²)

Dove i rappresenta l’ipotenusa, c₁ rappresenta il cateto minore e c₂ rappresenta il cateto maggiore.

Area dei triangoli rettangoli: Cateti e altezza relativa all’ipotenusa – YouTube

Ipotenusa del triangolo rettangolo con area e altezza

Un’altra formula per il calcolo dell’ipotenusa è:

i = (2S)/(h)

Dove i rappresenta l’ipotenusa, S rappresenta l’area del triangolo e h rappresenta l’altezza del triangolo relativa all’ipotenusa.

Ipotenusa del triangolo rettangolo con cateto minore e sua proiezione

Una terza formula per il calcolo dell’ipotenusa è:

i = (c₁²)/(p₁)

Dove i rappresenta l’ipotenusa, c₁ rappresenta il cateto minore e p₁ rappresenta la proiezione del cateto minore sull’ipotenusa.

Ipotenusa del triangolo rettangolo con cateto maggiore e sua proiezione

Un’altra formula per il calcolo dell’ipotenusa è:

i = (c₂²)/(p₂)

Dove i rappresenta l’ipotenusa, c₂ rappresenta il cateto maggiore e p₂ rappresenta la proiezione del cateto maggiore sull’ipotenusa.

Ipotenusa del triangolo rettangolo con proiezioni dei due cateti

Un’altra formula per il calcolo dell’ipotenusa è:

i = p₁+p₂

Dove i rappresenta l’ipotenusa, p₁ rappresenta la proiezione del cateto minore sull’ipotenusa e p₂

Esercizi svolti sull’ipotenusa del triangolo rettangolo

Per calcolare l’ipotenusa di un triangolo rettangolo possiamo utilizzare diverse formule dirette. Di seguito, vediamo un esempio di applicazione della formula per il calcolo dell’ipotenusa con i due cateti.

Calcolo ipotenusa triangolo rettangolo con i cateti

Dal teorema di Pitagora sappiamo che l’area del quadrato costruito sull’ipotenusa è equivalente alla somma delle aree dei quadrati costruiti sui cateti. In formule:

i^2 = c₁²+c₂²

Estraendo la radice quadrata di entrambi i membri otteniamo la formula per calcolare la misura dell’ipotenusa da quella dei cateti:

i = √(c₁²+c₂²)

Esempio

Supponiamo che i due cateti di un triangolo rettangolo misurino 13,3 cm e 15,6 cm. Calcoliamo la misura dell’ipotenusa.

i = √(c₁²+c₂²) = √((13,3 cm)²+(15,6 cm)²) = √(176,89 cm²+243,36 cm²) = √(420,25 cm²) = 20,5 cm

Quindi, la misura dell’ipotenusa del triangolo rettangolo è di 20,5 cm.

Calcolo ipotenusa triangolo rettangolo con area e altezza

Un’altra formula diretta per il calcolo dell’ipotenusa di un triangolo rettangolo è quella che utilizza l’area e l’altezza del triangolo. Invertendo la formula per il calcolo dell’area del triangolo rettangolo:

S = (i×h)/(2)

Si può ottenere la misura dell’ipotenusa moltiplicando l’area per 2 e dividendola per la misura dell’altezza:

i = (2S)/(h)

Esempio

Supponiamo che l’area di un triangolo rettangolo sia di 36 metri quadrati e che l’altezza sia di 5 metri. Calcoliamo la misura dell’ipotenusa:

i = (2S)/(h) = (2×(36 m²))/(5 m) = (72 m²)/(5 m) = 14,4 m

Quindi, la misura dell’ipotenusa del triangolo rettangolo è di 14,4 metri.

Calcolo ipotenusa triangolo rettangolo con cateto e proiezione del cateto sull’ipotenusa

Per un triangolo rettangolo vale il primo teorema di Euclide, secondo cui ciascun cateto è il medio proporzionale tra l’ipotenusa e la sua proiezione sull’ipotenusa:

i:c₁ = c₁:p₁ ; i:c₂ = c₂:p₂

Applicando la proprietà fondamentale delle proporzioni si ottengono le due formule che permettono di determinare l’ipotenusa partendo dalle misure del cateto e della sua proiezione:

i = (c₁²)/(p₁) ; i = (c₂²)/(p₂)

Esempio

Supponiamo che il cateto minore di un triangolo rettangolo misuri 3 decimetri e che la sua proiezione sull’ipotenusa sia di 1,8 decimetri. Calcoliamo la misura dell’ipotenusa:

i = (c₁²)/(p₁) = ((3 dm)²)/(1,8 dm) = (9 dm²)/(1,8 dm) = 5 dm

Quindi, la misura dell’ipotenusa del triangolo rettangolo è di 5 decimetri.

Calcolo ipotenusa triangolo rettangolo con le proiezioni dei due cateti sull’ipotenusa

Un’altra formula diretta per il calcolo dell’ipotenusa di un triangolo rettangolo è quella che utilizza le proiezioni dei due cateti sull’ipotenusa. Se con i dati forniti dal testo del problema si riesce a risalire alle misure delle due proiezioni dei cateti, dalla loro somma si ottiene la lunghezza dell’ipotenusa:

i = p₁+p₂

Esempio

Supponiamo che la proiezione del cateto maggiore sull’ipotenusa di un triangolo rettangolo sia di 25 millimetri e che l’altezza misuri 15 millimetri. Troviamo la lunghezza dell’ipotenusa:

Dal secondo teorema di Euclide sappiamo che l’altezza di un triangolo rettangolo è il medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa:

p₁:h = h:p₂

Poiché conosciamo la misura della proiezione del cateto maggiore:

p₂ = 25 mm

E la misura dell’altezza:

h = 15 mm

Possiamo ricavare la proiezione del cateto minore applicando la proprietà fondamentale delle proporzioni:

h² = p₁×p₂ ; p₁ = (h²)/(p₂) = ((15 mm)²)/(25 mm) = (225 mm²)/(25 mm) = 9 mm

Dalla somma delle misure delle proiezioni dei due cateti si ricava l’ipotenusa:

i = p₁+p₂ = 9 mm+25 mm = 34 mm

Quindi, la lunghezza dell’ipotenusa del triangolo rettangolo è di 34 millimetri.

Calcolo ipotenusa di un triangolo rettangolo isoscele (con angoli acuti di 45°)

Un triangolo rettangolo isoscele ha i due cateti congruenti:

c₁ = c₂ = c

Equivale alla metà di un quadrato, il cui lato ha la stessa misura dei cateti e la cui diagonale è l’ipotenusa. Calcolare la misura dell’ipotenusa di un triangolo rettangolo isoscele equivale quindi a determinare la misura della diagonale di un quadrato, che si ottiene moltiplicando il lato per la radice quadrata di 2:

i = √(2)c

Esempio

Troviamo l’ipotenusa di un triangolo rettangolo isoscele il cui cateto misura 7 centimetri:

i = √(2)c = √(2)×(7 cm) = 7√(2) cm ≃ 9,9 cm

Quindi, la lunghezza dell’ipotenusa del triangolo rettangolo isoscele è di circa 9,9 centimetri.

Calcolo ipotenusa triangolo rettangolo con angoli acuti di 30° e 60°

In un triangolo 30 60 90 per determinare l’ipotenusa basta conoscere la misura di uno dei due cateti e applicare una tra le seguenti formule:

i = 2c₁ ; i = (2c₂)/(√(3))

Esempio

Supponiamo che gli angoli acuti di un triangolo rettangolo siano ampi 30° e 60° e che il cateto minore sia di 5,6 metri. Calcoliamo la lunghezza dell’ipotenusa:

i = 2c₁ = 2×(5,6 m) = 11,2 m

Quindi, la lunghezza dell’ipotenusa del triangolo rettangolo è di 11,2 metri.

Fonte: YouMath.it

Stai guardando: IPOTENUSA DEL TRIANGOLO RETTANGOLO: DEFINIZIONE, FORMULE ED ESEMPI