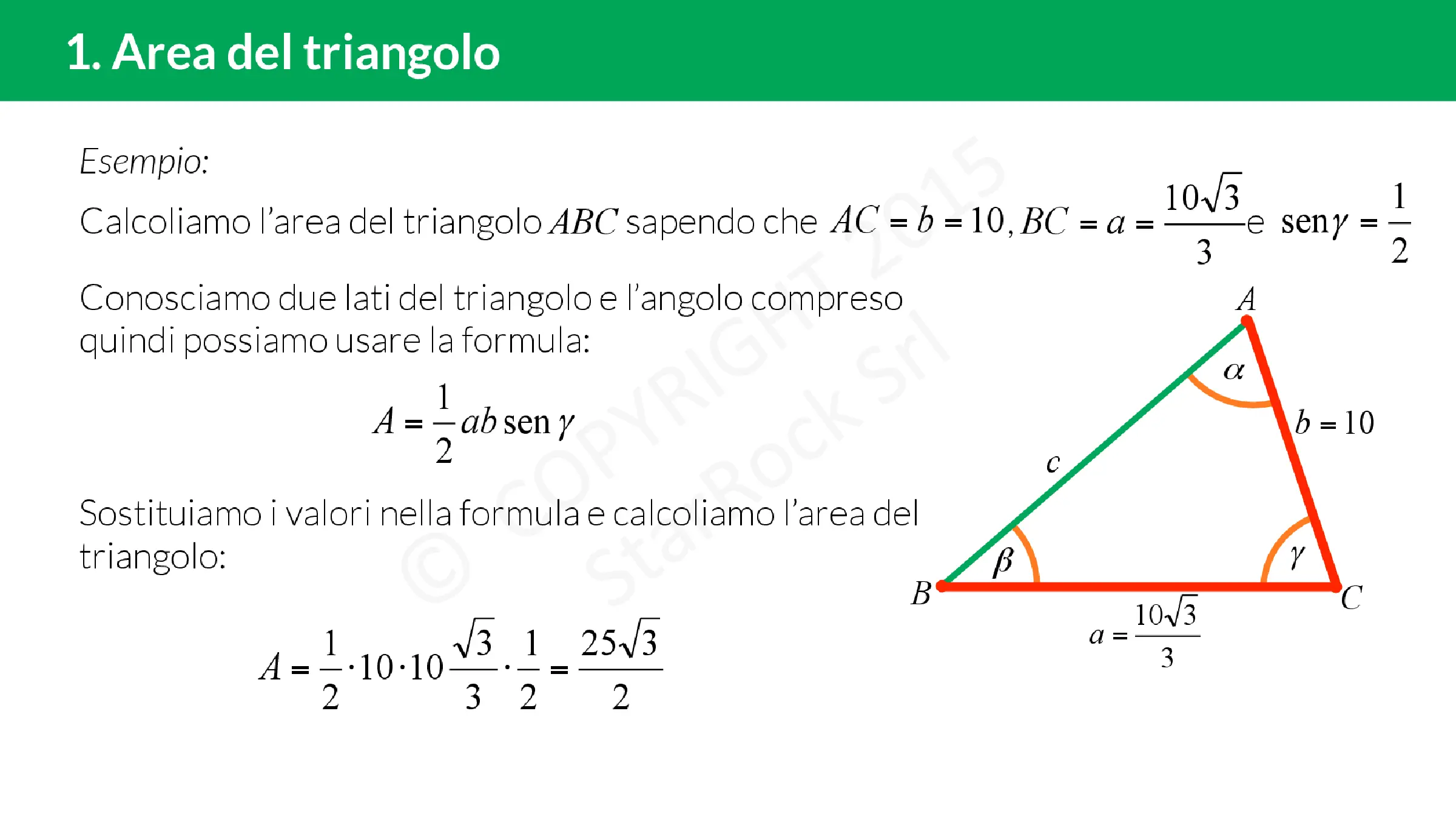
AREA DEL TRAPEZIO: FORMULE ED ESERCIZI SVOLTI
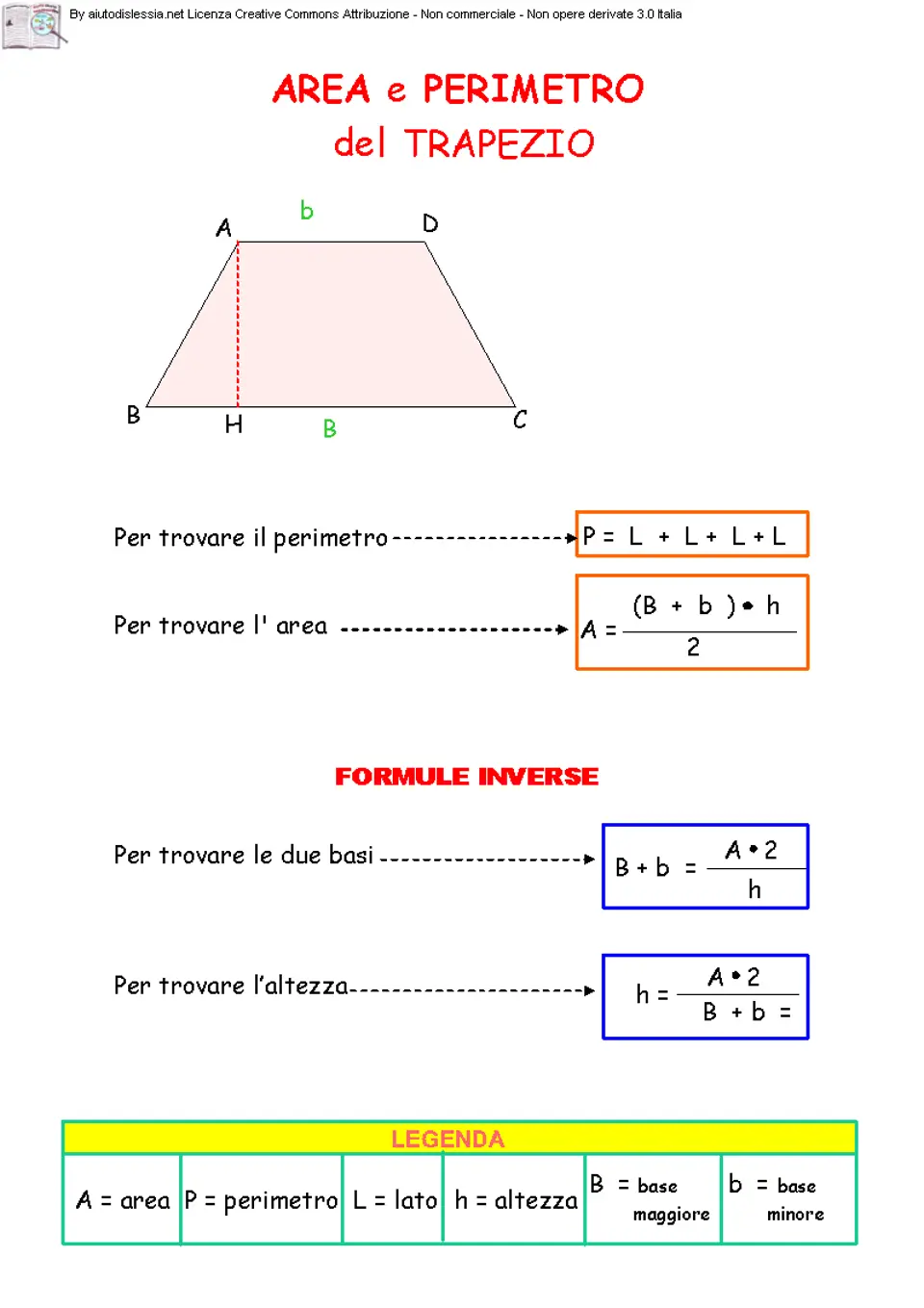
L’area del trapezio viene calcolata utilizzando la formula A=(b+B)·h/2, dove b e B sono le due basi del trapezio e h rappresenta l’altezza. L’area rappresenta la misura della superficie compresa all’interno dei quattro lati del trapezio. Questa formula permette di calcolare facilmente l’area di un trapezio senza dover conoscere la lunghezza dei lati obliqui.

Formula per l’area del trapezio
Indipendentemente dal tipo di trapezio considerato, l’area può essere calcolata utilizzando la stessa formula:
A = ((b+B)×h)/(2)
dove A rappresenta l’area, b la lunghezza della base minore, B la lunghezza della base maggiore e h l’altezza del trapezio.
Tuttavia, ogni tipo di trapezio ha proprietà specifiche che consentono di calcolare le lunghezze delle basi e dell’altezza in modo diverso. Di seguito sono riportate le proprietà specifiche per i trapezi isosceli, scaleni e rettangoli.
Trapezi Isosceli
Un trapezio isoscele ha due lati obliqui di uguale lunghezza e due angoli opposti di uguale ampiezza. Per calcolare l’area di un trapezio isoscele, è possibile utilizzare la formula generale e sostituire la lunghezza della base minore e maggiore con la stessa misura, indicata con b, e utilizzare la formula:
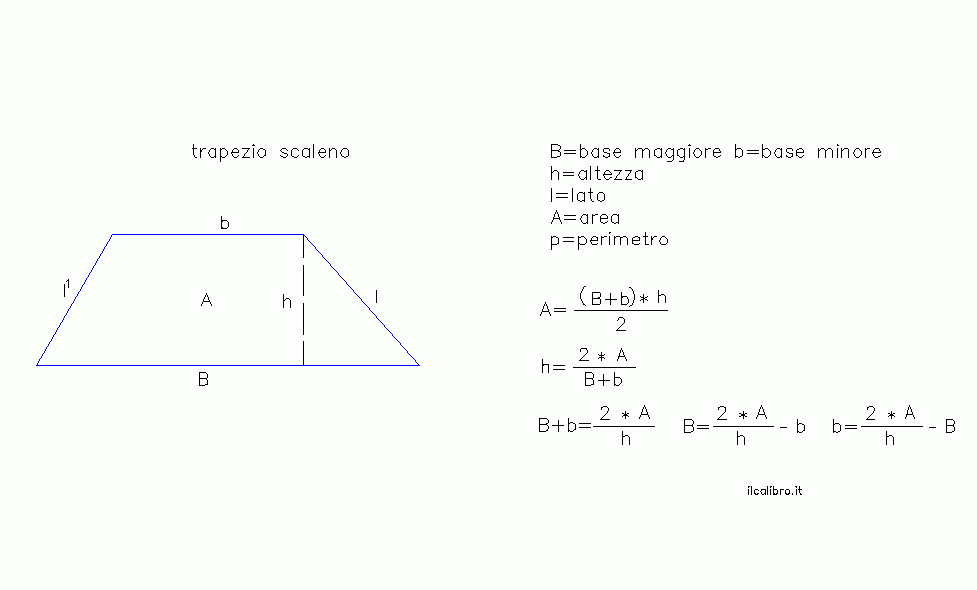
A = (b×h)
Trapezi Scaleni
Un trapezio scaleno ha le quattro lunghezze dei lati diverse e gli angoli opposti non hanno la stessa ampiezza. Per calcolare l’area di un trapezio scaleno, è possibile utilizzare la formula generale e determinare la lunghezza delle basi e dell’altezza utilizzando il teorema di Pitagora.
L’area del trapezio: teoria ed esercizi – Geometria – Secondaria di Primo Grado – YouTube
Trapezi Rettangoli
Un trapezio rettangolo ha due angoli retti e due lati obliqui di uguale lunghezza. Per calcolare l’area di un trapezio rettangolo, è possibile utilizzare la formula generale e sostituire la lunghezza della base minore e maggiore con la stessa misura, indicata con b, e utilizzare la formula:
A = (b×h)
Esercizi svolti sull’area del trapezio
In questo articolo sono riportati alcuni esercizi risolti sul calcolo dell’area del trapezio, ognuno con le relative spiegazioni dettagliate delle soluzioni.
Esercizio 1
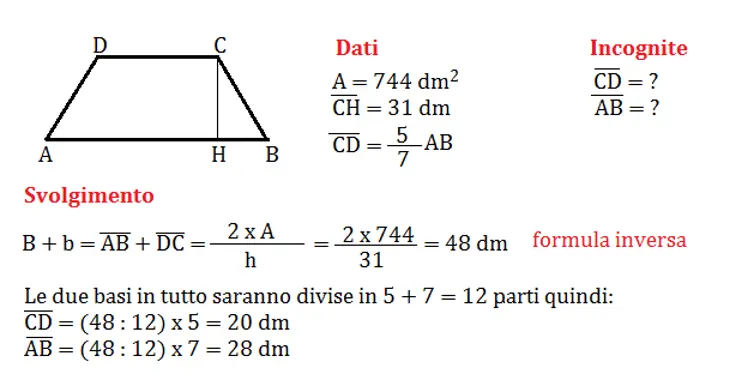
Data la somma delle basi di un trapezio di 15 cm e la loro differenza di 3 cm, si richiede di calcolare l’area del trapezio sapendo che l’altezza è la metà della base minore.
Svolgimento: calcoliamo la misura delle basi utilizzando la somma e la differenza tra le basi del trapezio. Rappresentiamo le due basi B e b graficamente, e ricaviamo la loro differenza.
Dalla rappresentazione grafica, si ottiene che:
- b = ((b+B)-3 cm)/(2) = (15 cm-3 cm)/(2) = 6 cm
- B = b+3 cm = 6 cm+3 cm = 9 cm
Calcoliamo ora l’altezza:
- h = (1/2)b = (1/2)×(6 cm) = 3 cm
Infine, calcoliamo l’area del trapezio utilizzando la formula:
- A = ((b+B)×h)/2 = ((15 cm)×(3 cm))/2 = (45 cm2)/2 = 22,5 cm2
In alternativa, per trovare la misura delle basi, avremmo potuto ricorrere alle equazioni. Sapendo che:
- b+B = 15 cm
- B-b = 3 cm
Dalla seconda relazione si può ricavare il valore della base maggiore in funzione della base minore:
- B = b+3 cm
Per poi sostituire nella prima relazione:
- b+b+3 cm (B) = 15 cm
E ottenere un’equazione di primo grado nell’incognita b:
- b+b+3 cm = 15 cm
Risolvendola si ricava la lunghezza della base minore:
- b+b = 15 cm-3 cm
- 2b = 12 cm
- b = (12 cm)/2 = 6 cm
E di conseguenza:
- B = b+3 cm = 6 cm+3 cm = 9 cm
Esercizio 2
Data la lunghezza delle due basi di un trapezio isoscele di 13 m e 7 m
Fonte: YouMath
Stai guardando: AREA DEL TRAPEZIO: FORMULE ED ESERCIZI SVOLTI