NOTAZIONE SCIENTIFICA DI UN NUMERO

La notazione scientifica, conosciuta anche come notazione esponenziale, consente di esprimere un numero in modo conciso come prodotto tra un numero decimale compreso tra 1 e 10, e una potenza di 10 con un esponente intero. Questo metodo di scrittura numerica è utile per rappresentare numeri molto grandi o molto piccoli in modo più semplice e compatto.

In pratica, per scrivere un numero in notazione scientifica, si sposta la virgola a destra o a sinistra fino a quando il primo cifra significativa si trova a sinistra della virgola, quindi si moltiplica per una potenza di 10 corrispondente allo spostamento effettuato.
La notazione scientifica di un numero
In matematica, la notazione scientifica permette di scrivere un numero in cui compare una sequenza molto lunga di zeri in forma compatta.
Un numero è scritto in notazione scientifica se è della forma:
a × 10n
dove a è un numero compreso tra 1 (incluso) e 10 (escluso), che non termina per zero, e n è un qualsiasi numero intero positivo o negativo.
Esempi sulla notazione scientifica
Ecco alcuni esempi di numeri scritti in notazione scientifica:
- 4,9 × 105
- 9,99 × 10-45
- 5,786 × 1013
Questi sono numeri scritti in notazione scientifica.
Al contrario, i seguenti numeri non sono in notazione scientifica:
- 6,80 × 106 (ha uno zero come ultima cifra)
- 0,9 × 10-23 (è minore di 1)
- 17,762 × 10-3 (è maggiore di 10)
Notazione scientifica – YouTube
Dalla notazione normale alla notazione scientifica di un numero naturale
Per scrivere i numeri naturali in notazione scientifica, è necessario seguire i seguenti passaggi:
- Contare il numero di cifre che formano il numero naturale, esclusa la prima cifra. Questo numero viene chiamato esponente ed è l’ordine di grandezza del numero.
- Aggiungere una virgola dopo la prima cifra a sinistra.
- Scrivere tutte le cifre rimanenti (se ci sono). Se alla fine del numero c’è una sequenza di zeri, non la trascriviamo.
- Moltiplicare per 10 elevato all’esponente.
Ad esempio, consideriamo il numero 706.000.000. Contiamo il numero di cifre dalla seconda all’ultima:
ci sono 8 cifre. Pertanto, il numero 706.000.000 scritto in notazione scientifica sarà:
7,06 × 108
Adesso, proviamo a scrivere in notazione scientifica i seguenti numeri naturali:
- 123.000.000
- 2.105.000.000.000
- 10.000.000.000.000.000
Soluzioni
123.000.000 = 1,23 × 108
2.105.000.000.000 = 2,105 × 1012
10.000.000.000.000.000 = 1 × 1016
Notazione scientifica di un numero decimale
Supponiamo ora di dover scrivere un numero decimale avente una lunga sequenza di zeri in forma compatta. In questo caso, ricorreremo alla notazione scientifica. Il procedimento per scrivere i numeri decimali in notazione scientifica è simile a quello visto per i numeri naturali.
Consideriamo il numero decimale 0,0000015. Per scriverlo in notazione scientifica, dobbiamo:
- Individuare, partendo da sinistra e procedendo verso destra, la prima cifra non nulla. Nel nostro caso sarà 1: 0,0000015.
- Posizionare la virgola dopo la cifra trovata e, nella notazione scientifica, riportare tutte le cifre successive alla virgola. Pertanto, avremo: 1,5 × 10spadesuit.
- Per trovare il valore di spadesuit, che rappresenta l’ordine di grandezza, bisogna contare il numero di cifre dalla virgola di partenza fino al punto in cui andremo a inserire la nuova virgola. Tale numero sarà la potenza del 10. Attenzione: nel caso dei numeri decimali minori di 1, l’esponente sarà un numero negativo.
- Scrivere il numero in notazione scientifica: 0,0000015 = 1,5 × 10-6.
Proviamo a scrivere in notazione scientifica i seguenti numeri decimali:
- 0,000000506
- 0,00012
- 0,00000000001002
Soluzioni
0,000000506 = 5,06 × 10-7
0,00012 = 1,2 × 10-4
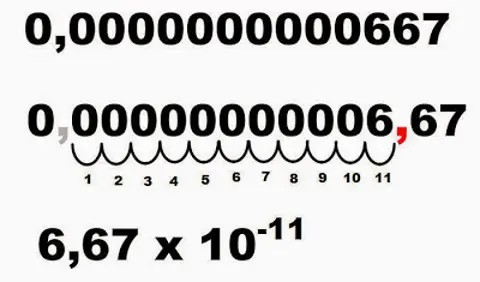
0,00000000001002 = 1,002 × 10-11
Dalla notazione scientifica a quella standard
Per scrivere un numero in notazione scientifica in forma standard, bisogna ricordare come la moltiplicazione di un numero per una potenza del 10 può comportare lo spostamento della virgola di una certa quantità di posti:
- Moltiplicare per 10 equivale ad aggiungere uno zero o spostare la virgola verso destra di un posto.
- Moltiplicare per 102 comporterà lo spostamento della virgola verso destra o l’aggiunta di due zeri fino a “coprire 2 posti”.
- Moltiplicare per 103 significa aggiungere 3 zeri o spostare la virgola verso destra di 3 posti, e così via.
- Moltiplicare per 10-1, 10-2, 10-3 comporterà lo spostamento della virgola verso sinistra di 1, 2, 3… posti.
Ad esempio, per scrivere in forma standard i seguenti numeri in notazione scientifica:
- 1 × 106
- 1,3 × 105
- 8,73 × 10-5
- 7,302 × 10-7
Avremo, rispettivamente:
- 1 × 106 = 1.000.000
- 1,3 × 105 = 130000
- 8,73 × 10-5 = 0,0000873
- 7,302 × 10-7 = 0,0000007302
In pratica, sulla calcolatrice la notazione scientifica può essere indicata nei risultati nella forma:
- numero.e±esponente
- numero exp±esponente
Ad esempio:
- 1,347 × 1034 → 1,347.e+34
- 0,54 × 10-5 → 0,54.e-5
- 7,4 × 108 → 7,4 exp+8
- 0,3 × 10-14 exp-14
Fonte: YouMath
Stai guardando: NOTAZIONE SCIENTIFICA DI UN NUMERO