DEFINIZIONE DI FUNZIONE
Iniziamo il nostro studio dell’Analisi introducendo la definizione fondamentale di funzione e approfondendo il concetto di funzioni reali di variabile reale. Prima di procedere, è importante ricordare la definizione di funzione tra due insiemi qualsiasi, perciò effettueremo un breve ripasso con tutti i commenti del caso.

Successivamente, esporremo la definizione mettendo in evidenza le difficoltà che possono insorgere durante lo studio per la prima volta. Al fine di facilitare la comprensione, useremo parole semplici in aggiunta al linguaggio simbolico.
Definizione di funzione tra due insiemi
Introduzione
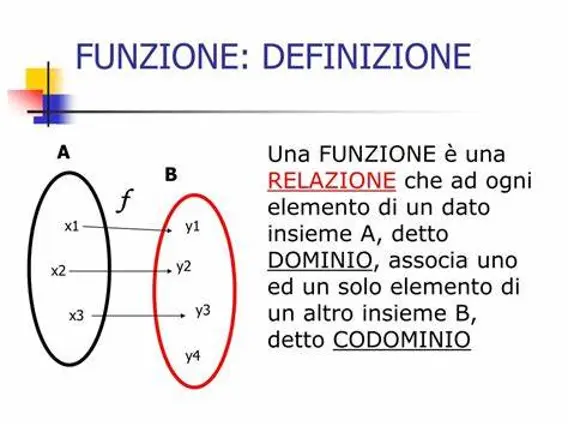
Una funzione tra due insiemi è una corrispondenza tra i loro elementi che associa ad ogni elemento dell’insieme di partenza esattamente un elemento dell’insieme di arrivo.
Definizione
Formalmente, una funzione $f:A \rightarrow B$ è una regola che associa ad ogni elemento $a \in A$ un unico elemento $b \in B$. Questo significa che ogni elemento di $A$ deve avere esattamente una freccia che parte da esso, e ogni freccia deve puntare a un unico elemento di $B$. In notazione matematica, questo si scrive come $ \forall a \in A \exists ! b \in B$ tale che $f(a) = b$, dove $\forall$ significa “per ogni”, $\exists !$ significa “esiste un unico” e $f(a) = b$ significa che $a$ viene associato a $b$ attraverso la funzione $f$.
Diagrammi di funzioni
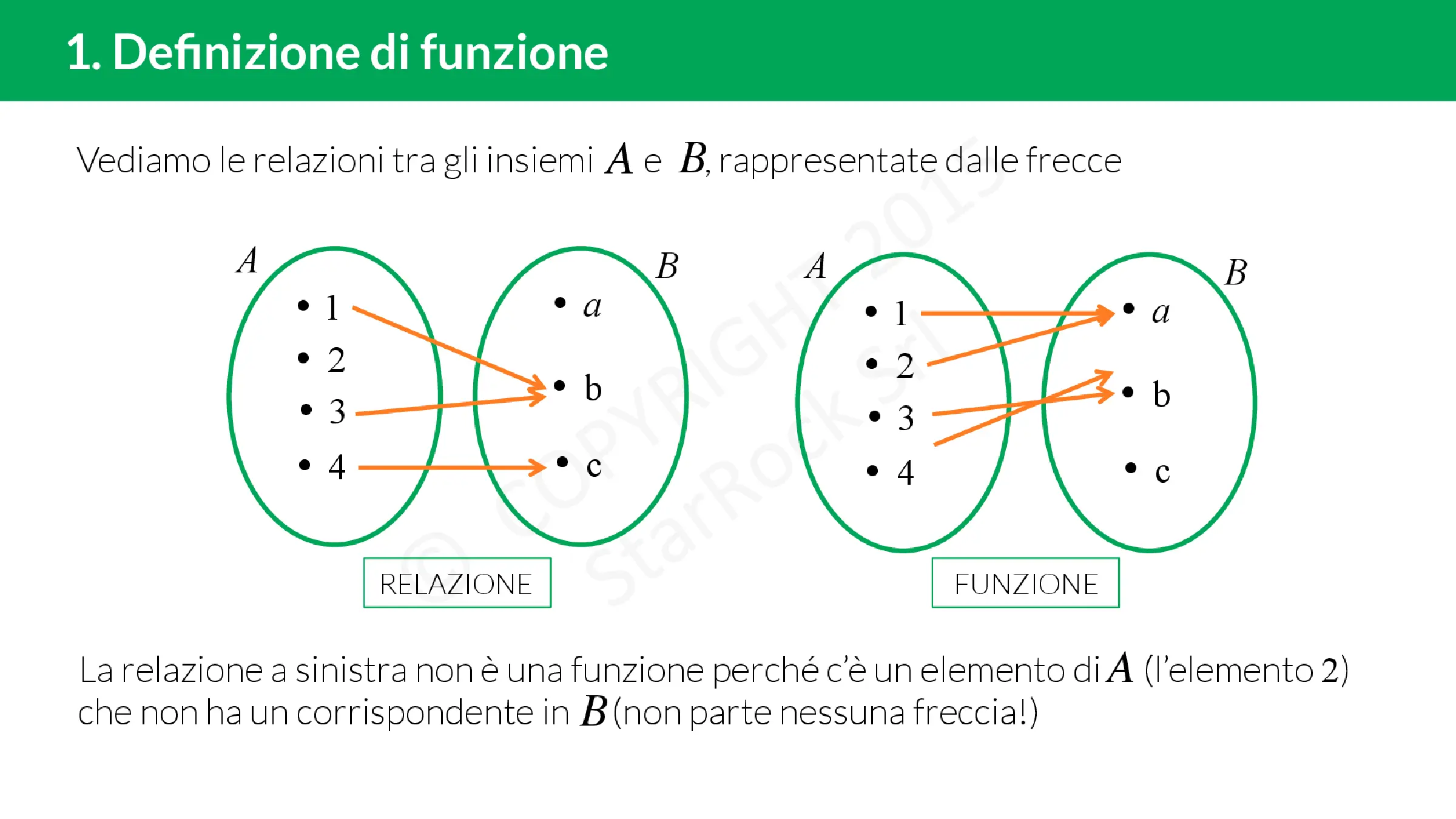
Un modo comune per rappresentare una funzione è attraverso un diagramma a frecce. Ad esempio, la funzione $f:{1,2,3} \rightarrow {a,b,c}$ che associa ad ogni numero il corrispondente carattere dell’alfabeto può essere rappresentata nel seguente modo:
Tuttavia, un diagramma a frecce non rappresenta una funzione se non rispetta le regole descritte sopra. Ad esempio, il seguente diagramma non rappresenta una funzione perché l’elemento 4 dell’insieme di partenza non ha nessuna freccia che parte da esso e l’elemento 2 dell’insieme di partenza è associato a due elementi distinti di $B$:
Funzioni – Introduzione, Dominio e Codominio, Insieme Immagine – YouTube
Conclusioni
In sintesi, una funzione tra due insiemi è una corrispondenza che associa ad ogni elemento dell’insieme di partenza un unico elemento dell’insieme di arrivo, rispettando le regole descritte sopra. Questo concetto è molto importante in matematica e ha numerose applicazioni in molte aree della scienza e dell’ingegneria.
Fonte: Math Planet
Nomenclatura delle funzioni
Introduzione
Nella definizione di funzione tra due insiemi, è possibile assegnare dei nomi comodi ai vari elementi coinvolti per semplificare la scrittura e la comprensione.
Nomi degli elementi di una funzione
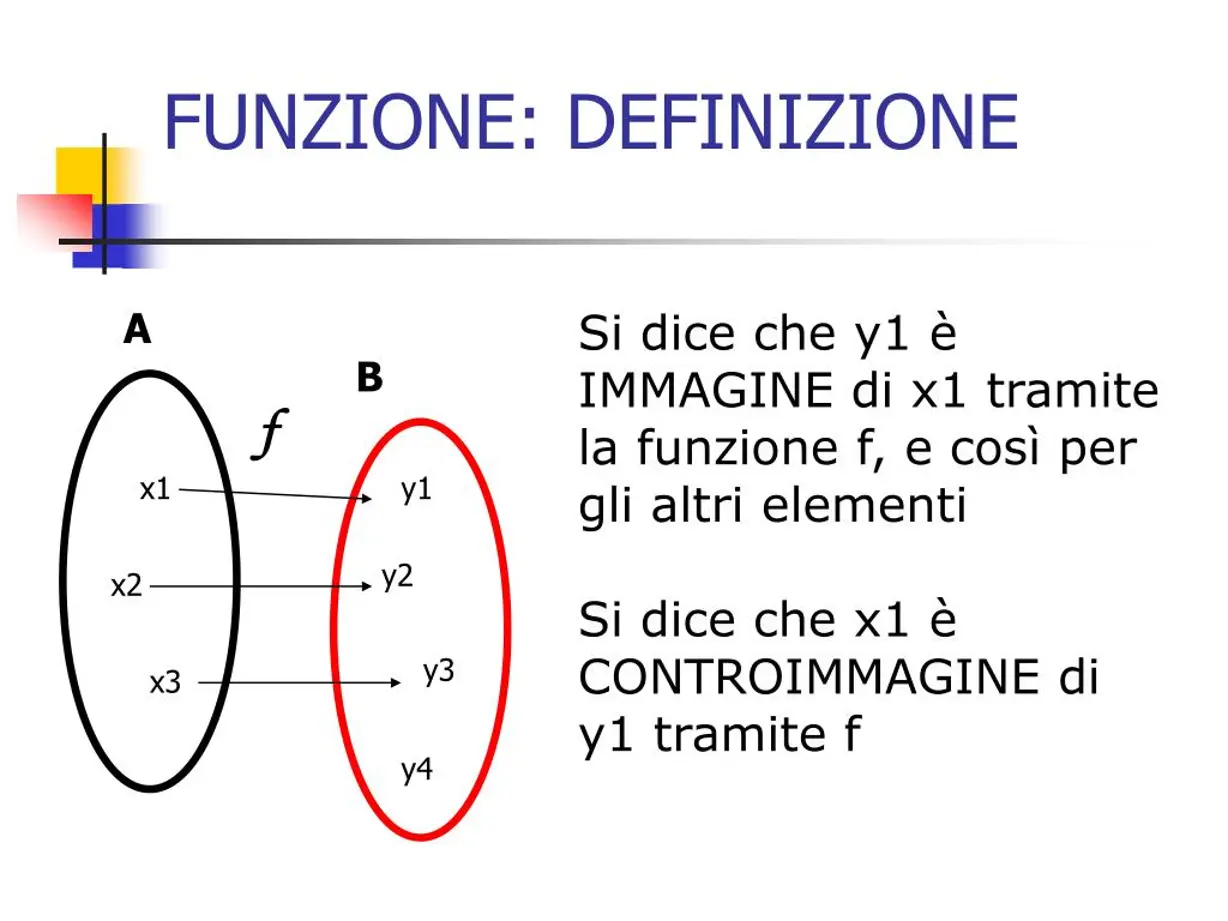
Supponiamo di avere una funzione $f:A \rightarrow B$ che associa ad ogni elemento $a \in A$ un elemento $b \in B$. Se un elemento $b$ di $B$ viene raggiunto da una freccia che parte da un elemento $a$ di $A$ attraverso la funzione $f$, ovvero $f(a) = b$, allora chiamiamo:
- $b$ l’immagine di $a$ mediante la funzione $f$
- $a$ la preimmagine (o controimmagine) di $b$ mediante $f$.
Domino, codominio e immagine di una funzione
Diciamo che l’insieme degli elementi ai quali è applicata la funzione $f$, ovvero l’insieme di partenza $A$, è il dominio della funzione $f$ o insieme di definizione di $f$. L’insieme di arrivo $B$ prende il nome di codominio. Il sottoinsieme degli elementi di $B$ che vengono raggiunti dalle frecce viene detto immagine della funzione $f$ e può coincidere o meno con il codominio $B$.
Conclusioni
In sintesi, la nomenclatura delle funzioni permette di semplificare la scrittura e la comprensione delle funzioni tra due insiemi. Attraverso i nomi degli elementi di una funzione, possiamo riferirci in modo più chiaro e preciso ad essi. Inoltre, definendo il dominio, il codominio e l’immagine di una funzione, possiamo stabilire con esattezza quali elementi vengono coinvolti dalla funzione e come sono collegati tra loro.
Fonte: Lezioni di Matematica
Legge di una funzione ed esempi sulle funzioni
Introduzione
La legge di una funzione tra due insiemi è la regola che definisce la corrispondenza tra i loro elementi. Questa regola può essere espressa in vari modi: a parole, mediante tabulazione insiemistica, mediante diagrammi e grafici, o mediante un’espressione analitica. Vediamo alcuni esempi.
Legge di una funzione a parole
Per descrivere la legge di una funzione a parole, si elencano gli insiemi $A$ e $B$ e si definisce la corrispondenza esplicitamente. Ad esempio, dati gli insiemi $A={Marco,Luca,Giovanni}$ e $B={Laura,Martina,Elena}$, la legge che associa Laura a Marco, Martina a Luca ed Elena a Giovanni è una funzione.
Legge di una funzione mediante tabulazione insiemistica
Per rappresentare la legge di una funzione mediante tabulazione insiemistica, si riportano in una tabella gli elementi del dominio e le rispettive immagini in due colonne distinte. Ogni riga definisce la corrispondenza tra l’elemento del dominio e la relativa immagine. Ad esempio, la classifica del campionato di calcio di Serie A al termine di ogni giornata definisce una funzione che associa ad ogni squadra un punteggio.
Legge di una funzione mediante diagrammi
La rappresentazione mediante diagrammi si basa sull’utilizzo dei diagrammi di Eulero Venn, con particolare riferimento agli insiemi costituiti da un numero finito di elementi, o eventualmente sull’utilizzo di grafici. Ad esempio, la funzione che associa ad ogni numero il suo quadrato può essere rappresentata graficamente nel seguente modo:
Legge di una funzione mediante espressione analitica
La definizione di una funzione mediante un’espressione analitica è possibile solamente nel caso di alcune leggi tra insiemi numerici. Solitamente l’espressione analitica di una funzione si indica con la scrittura $f:A \rightarrow B; f:x \rightarrow y, y=f(x)$ e consiste nell’esprimere la legge mediante una serie di funzioni elementari e operazioni algebriche di base. Ad esempio, la funzione che associa ad ogni numero il suo doppio può essere definita analiticamente come $f:\mathbb{N} \rightarrow \mathbb{N}, f(x)=2x$.
Conclusioni
In sintesi, la legge di una funzione tra due insiemi può essere rappresentata in vari modi, a seconda delle necessità e della comodità. La rappresentazione a parole, mediante tabulazione insiemistica, mediante diagrammi e grafici, o mediante un’espressione analitica, sono tutte equivalenti tra loro e possono essere utilizzate a seconda delle circostanze.
La rappresentazione più basilare possibile della legge di una funzione
Introduzione
Ogni funzione tra due insiemi può essere rappresentata in modo rigoroso e univoco mediante prodotto cartesiano. In particolare, ogni funzione può essere rappresentata (o addirittura definita) come un particolare sottoinsieme del prodotto cartesiano tra il dominio e il codominio.
Esempio
Consideriamo l’insieme $A$ delle tre regioni più popolose d’Italia (Lombardia, Campania, Lazio) e l’insieme $B$ costituito da quattro elementi: Milano, Napoli, Roma e Torino. Chiamiamo $f$ la funzione che associa ad ogni elemento di $A$ il relativo capoluogo.
La legge proposta individua una funzione perché ne soddisfa la definizione. L’immagine è data dall’insieme ${Milano, Napoli, Roma}$ ed è un sottoinsieme del codominio. Se consideriamo il prodotto cartesiano tra il dominio e il codominio
$$(A \times B) = { (Lombardia,Milano) , (Lombardia,Napoli) , (Lombardia,Roma) , (Lombardia, Torino), (Campania,Milano) , (Campania,Napoli) , (Campania,Roma) , (Campania,Torino), (Lazio,Milano) , (Lazio,Napoli) , (Lazio,Roma) , (Lazio,Torino) }$$
allora possiamo descrivere la funzione mediante un unico sottoinsieme del prodotto cartesiano
$$f = { (Lombardia,Milano) , (Campania,Napoli) , (Lazio,Roma) }$$
che rappresenta in modo completo e univoco la funzione $f$.
Conclusioni
La rappresentazione di una funzione mediante prodotto cartesiano è la più basilare possibile e permette di descrivere in modo rigoroso e univoco qualsiasi funzione tra due insiemi. Tale rappresentazione è particolarmente utile per le applicazioni pratiche, come l’implementazione di funzioni in un computer, ma anche per la dimostrazione di proprietà teoriche delle funzioni.
Funzioni reali di variabile reale
Le funzioni reali di variabile reale sono le protagoniste dell’Analisi Matematica. Sono funzioni per le quali:
- l’insieme di definizione A è un sottoinsieme dell’insieme dei numeri reali R, che eventualmente può coincidere con esso (funzione di variabile reale). Gli elementi del dominio prendono spesso e volentieri il nome di punti, pur trattandosi di un abuso di linguaggio;
- l’insieme di arrivo B, ossia il codominio, è l’insieme dei numeri reali R (funzione reale o funzione a valori reali).
A ⊆ R , B = R e f:A ⊆ R → R. Notate che deve valere sempre con la stessa regola: non è possibile avere una funzione che a un valore del dominio associ due o più elementi del codominio.
Esempi di funzioni reali
Ecco alcuni esempi di funzioni reali:
- La funzione identità: f(x) = x. Questa è una tra le più semplici funzioni, infatti dato un numero reale x lo restituisce esattamente tale e quale.
- La funzione f(x) = 3x+2. Le funzioni di questa forma sono dette funzioni lineari; il loro grafico corrisponde a quello di una retta.
- La funzione f(x) = (x^2)/(x+2). A differenza delle altre due, questa è una funzione che non è definita ovunque sull’insieme dei numeri reali. Essendo infatti in presenza di un denominatore, per individuare il dominio dobbiamo escludere il valore che lo annulla: non si può dividere per zero!
Come valutare una funzione in un punto
Per valutare una funzione reale di variabile reale in un punto, è sufficiente sostituire il valore del punto in cui si vuole valutare la funzione al posto della variabile indipendente (generalmente indicata con x), svolgere i calcoli necessari e ottenere l’immagine corrispondente mediante la funzione. È importante notare che ha senso valutare una funzione solo nei punti in cui essa è definita.
Vediamo ora alcuni esempi sulla valutazione delle funzioni in alcuni punti.
La funzione identità
La funzione identità f(x) = x nei punti x = 0, x = 1, x = 2 ha come valori f(0) = 0, f(1) = 1 e f(2) = 2, ottenuti semplicemente sostituendo 0, 1 e 2 al posto della variabile x nella definizione della funzione.
Le valutazioni della funzione lineare
Consideriamo la funzione lineare f(x) = 3x+2. Per valutare questa funzione nei punti x = 1, x = 2, x = 3, sostituiamo rispettivamente 1, 2 e 3 al posto della variabile x nella definizione della funzione e otteniamo f(1) = 5, f(2) = 8 e f(3) = 11.
La funzione razionale
Consideriamo la funzione razionale f(x) = (x^2)/(x+2). Per valutare questa funzione nei punti x = 0, x = 1, x = 2, sostituiamo rispettivamente 0, 1 e 2 al posto della variabile x nella definizione della funzione e otteniamo f(0) = 0, f(1) = 1/3 e f(2) = 4/4 = 1.
Trucco per non sbagliare nella valutazione di una funzione
Per evitare errori di distrazione nella valutazione di una funzione, si può sostituire il punto racchiuso tra parentesi al posto della variabile indipendente x e svolgere successivamente i calcoli. In questo modo, si minimizza il rischio di errore.
Ad esempio, consideriamo la funzione f(x) = (x^2-5x+3)/((-x+6)^2) e valutiamola nel punto x = -2. Sostituendo -2 al posto di x nella definizione della funzione, otteniamo:
f(-2) = ((-2)^2-5·(-2)+3)/((-(-2)+6)^2) = (4+10+3)/(4^2) = 17/16
Stai guardando: DEFINIZIONE DI FUNZIONE