EQUAZIONI DI SECONDO GRADO

Le equazioni quadratiche sono equazioni di secondo grado in cui l’incognita ha un esponente di grado 2 e, talvolta, esponenti di grado inferiore. Dopo aver acquisito familiarità con le equazioni di primo grado, passiamo alle equazioni definite tramite polinomi. In questa lezione, ci concentreremo sulle equazioni di secondo grado, definendole e illustrando i principali metodi di risoluzione.

La formula del delta (o discriminante) è una formula risolutiva utilizzabile in ogni caso, quando disponiamo della forma normale dell’equazione. Tuttavia, sarà possibile utilizzare metodi risolutivi più immediati in alcuni casi particolari, grazie all’introduzione di una classificazione.
Equazioni di secondo grado: definizione e esempi
Le equazioni di secondo grado sono un tipo di equazioni polinomiali in cui l’incognita compare almeno una volta con esponente di grado 2 e tale che l’incognita compaia con grado massimo pari a 2. In altre parole, un’equazione ha grado 2 se uno dei due membri è un polinomio di grado 2 e l’altro membro è un polinomio di grado al più 2.
Ecco alcuni esempi di equazioni di secondo grado:
- x^2+5x+4 = 0
- x^2 = 4x
- x^2 = 1
- x-x^2 = 4+x-x^2
Forma normale delle equazioni di secondo grado
Per risolvere le equazioni di secondo grado in modo efficace, è utile definire la loro forma normale:

ax^2+bx+c = 0
Dove:
- a è detto coefficiente del termine di grado 2
- b è detto coefficiente del termine di grado 1
- c è detto coefficiente del termine di grado 0, o termine noto
La forma normale individua un’equazione di secondo grado a patto che risulti a ≠ 0. In caso contrario (a = 0), avremmo a che fare con un’equazione di primo grado se b ≠ 0, o con un’equazione senza incognita se b = 0.
Equazioni di secondo grado – YouTube
Risoluzione delle equazioni di secondo grado
Lo scopo dello studio delle equazioni di secondo grado è quello di risolvere qualsiasi equazione di secondo grado in forma normale o, eventualmente, qualsiasi equazione che sia stata ricondotta alla precedente forma normale. È importante notare che potrebbe capitare un’equazione come:
x^3+x^2 = x^3
Che all’apparenza sembrerebbe di terzo grado, ma che si riconduce facilmente a un’equazione di grado 2:
x^2 = 0
Per risolvere un’equazione di secondo grado in forma normale, si utilizzano le formule di soluzione, che sono:
x = (-b ± sqrt(b^2-4ac)) / 2a
Dove sqrt indica la radice quadrata e i segni ± indicano che si devono considerare entrambe le soluzioni.
È importante ricordare che la soluzione dell’equazione dipende dal segno del discriminante Δ = b^2 – 4ac:
- Se Δ > 0, l’equazione ha due soluzioni reali distinte;
- Se Δ = 0, l’equazione ha una sola soluzione reale doppia;
- Se Δ <
Numero di soluzioni di un’equazione di secondo grado in forma normale
Le equazioni di secondo grado in forma normale si presentano come:
ax2+bx+c = 0
dove a, b e c sono coefficienti reali e a ≠ 0.
Il numero di soluzioni dell’equazione dipende dal segno del discriminante Δ, che si calcola come:
Δ = b2-4ac
Discriminante positivo (Δ > 0)
Se il discriminante è positivo, l’equazione ammette due soluzioni distinte:
x1 = (-b+√Δ)/(2a) e x2 = (-b-√Δ)/(2a)
Le soluzioni sono due numeri reali e distinti:
S = {x1, x2}, con x1 ≠ x2
Discriminante nullo (Δ = 0)
Se il discriminante è nullo, l’equazione ammette una sola soluzione:
x1 = x2 = -b/(2a)
La soluzione è un numero reale:
S = {x1}
Si dice che l’equazione ammette una soluzione reale con molteplicità algebrica 2.
Discriminante negativo (Δ < 0)
Se il discriminante è negativo, l’equazione non ammette soluzioni reali:
not ∃ x∈R
Si dice che l’equazione è impossibile.
Metodi di risoluzione e classificazione delle equazioni di secondo grado
In matematica, le equazioni di secondo grado sono equazioni polinomiali di secondo grado in una variabile. Esistono sostanzialmente un metodo generale che permette di risolvere qualsiasi equazione di secondo grado e una serie di metodi più immediati, applicabili però solamente in alcuni casi particolari. Il punto di partenza è sempre la forma normale delle equazioni di secondo grado:
Forma normale delle equazioni di secondo grado
La forma normale delle equazioni di secondo grado è:
ax^2+bx+c = 0 con a ≠ 0
Casi particolari delle equazioni di secondo grado
Vediamo una panoramica completa sulla classificazione delle equazioni di secondo grado proponendo di volta in volta i metodi risolutivi ed esempi svolti per ciascun caso:
Caso 1: Equazione di secondo grado completa
Una equazione di secondo grado completa è dell’aspetto:
ax^2+bx+c = 0 con a ≠ 0, b ≠ 0 e c ≠ 0
Il metodo generale per risolvere queste equazioni è il seguente:
- Calcolare il discriminante: Δ = b^2 – 4ac
- Classificare l’equazione in base al valore del discriminante Δ:
- Se Δ > 0, l’equazione ha due soluzioni reali distinte.
- Se Δ = 0, l’equazione ha due soluzioni reali coincidenti.
- Se Δ < 0, l’equazione non ha soluzioni reali.
- Calcolare le soluzioni dell’equazione usando la formula risolutiva:
Caso 2: Equazione di secondo grado pura
Una equazione di secondo grado pura è dell’aspetto:
ax^2+c = 0 con a ≠ 0 e c ≠ 0
Il metodo risolutivo per queste equazioni consiste nel:
Calcolare le soluzioni dell’equazione usando la formula risolutiva:
x_1 = √(-c/a)
x_2 = -√(-c/a)
Caso 3: Equazione di secondo grado spuria
Una equazione di secondo grado spuria è dell’aspetto:
ax^2+b = 0 con a ≠ 0 e b ≠ 0
Il metodo risolutivo per queste equazioni consiste nel:
Calcolare la soluzione dell’equazione:
x = 0
Equazione di secondo grado completa
Un’equazione di secondo grado in forma normale in cui tutti i coefficienti sono diversi da zero è definita come equazione di secondo grado completa:
ax^2+bx+c = 0 con a ≠ 0, b ≠ 0, c ≠ 0
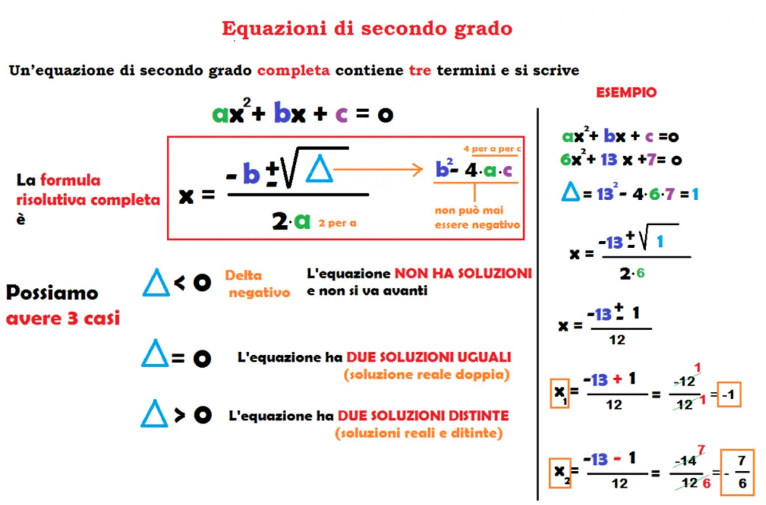
Il principale metodo per risolvere le equazioni di grado 2 complete è la formula risolutiva delle equazioni di secondo grado o formula del delta, che prevede di considerare una quantità caratteristica delle equazioni di secondo grado, il cosiddetto discriminante:
Δ = b^2-4ac
Il discriminante Δ viene anche indicato con la lettera greca maiuscola Δ.
La formula risolutiva per le equazioni di secondo grado è:
x1,2 = (-b±√(Δ))/(2a)
o esplicitamente
x1,2 = (-b±√(b^2-4ac))/(2a) → x1 = (-b-√(b^2-4ac))/(2a) ; x2 = (-b+√(b^2-4ac))/(2a)
Il simbolo ± va letto come più o meno ed è una scrittura sintetica per indicare che bisogna considerare due possibilità ugualmente valide: la prima si ottiene usando il segno + in luogo di ±, la seconda sostituendo ± con il segno -.
La formula risolutiva per le equazioni di secondo grado complete ha due aspetti estremamente interessanti:
Aspetto A: Applicabilità universale
La formula risolutiva può essere utilizzata sempre e comunque, anche per le equazioni di secondo grado non complete.
Aspetto B: Predizione delle soluzioni
La formula ci permette di capire il numero delle soluzioni dell’equazione ancor prima di applicarla. Guardando attentamente il secondo termine del numeratore:
(…±√(Δ))/(…)
Se analizziamo il segno del delta (positivo, negativo o nullo) possiamo capire velocemente che:
- Se il discriminante è positivo (Δ > 0) allora avremo due soluzioni reali distinte, infatti ci troviamo a sommare/sottrarre la radice di un numero positivo.
- Se il discriminante è nullo (Δ = 0) allora avremo due soluzioni reali coincidenti, infatti ci ritroveremo a sommare/sottrarre la radice di zero, che è zero.
- Se il discriminante è negativo (Δ < 0) allora la formula risolutiva
Esempi di equazioni di secondo grado complete
Le equazioni di secondo grado sono equazioni polinomiali in cui il termine di grado massimo è pari a due. Un’equazione di secondo grado completa è un’equazione in cui i coefficienti di tutti i termini sono diversi da zero. Ecco alcuni esempi:
x^2-3x+2 = 0
Per risolvere questa equazione, dobbiamo prima calcolare il delta:
Δ = b^2-4ac = (-3)^2-4·1·2 = 9-8 = 1 > 0
Poiché il discriminante è positivo, ci aspettiamo due soluzioni reali e distinte per l’equazione:
x_(1,2) = (-b±√(Δ))/(2a) = (-(-3)±√(1))/(2·1) = (3±1)/(2) = (3-1)/(2) = 1 ; (3+1)/(2) = (4)/(2) = 2
Quindi le soluzioni sono x_1 = 1, x_2 = 2.
x^2-2x+1 = 0
Per questa equazione, calcoliamo il discriminante:
Δ = b^2-4ac = (-2)^2-4·1·1 = 4-4 = 0
Pertanto, avremo due soluzioni reali e coincidenti:
x_(1,2) = (-b±√(Δ))/(2a) = (-(-2)±√(0))/(2·1) = (2±0)/(2) = (2)/(2) = 1
L’unica soluzione reale (con molteplicità algebrica 2) è x = 1.
x^2+x+1 = 0
Calcoliamo il delta dell’equazione:
Δ = b^2-4ac = 1^2-4·1·1 = 1-4 = -3 < 0
Poiché il delta è negativo, l’equazione non ha soluzioni reali.
Equazioni di secondo grado monomie
Un’equazione di secondo grado monomia è un’equazione di secondo grado in cui i coefficienti dei termini di grado 1 e 0 sono nulli, ossia b = 0 = c. Il metodo di risoluzione delle equazioni di secondo grado monomie è immediato e non richiede calcoli. Esse infatti ammettono sempre due soluzioni reali e coincidenti, entrambe nulle, quale che sia il valore di a ≠ 0:
x = 0
Se lo desideriamo, possiamo applicare la formula risolutiva per le equazioni complete:
x_(1,2) = (-b±√(b^2-4ac))/(2a) = (-0±√(0^2-4·a·0))/(2·a) = (0±0)/(2a)
Equazioni di secondo grado pure
Un’equazione di secondo grado pura è un’equazione di secondo grado in forma normale in cui il coefficiente del termine di grado 1 è nullo e il termine noto è diverso da zero: b = 0, c ≠ 0
Forma dell’equazione di secondo grado pura
L’equazione di secondo grado pura si presenta nella forma:
ax^2+c = 0 con a ≠ 0, c ≠ 0
Per risolvere un’equazione in questa forma, possiamo procedere al calcolo diretto delle eventuali soluzioni.
Formula risolutiva
Applicando la formula risolutiva per le equazioni di secondo grado complete nel caso delle monomie, otteniamo le seguenti soluzioni:
x_(1,2) = ±√((-c)/(a))
Dove:
- se a,c sono concordi, allora -(c)/(a) è negativo e l’equazione non ammette soluzioni reali (impossibile);
- se a,c sono discordi, allora -(c)/(a) è positivo e l’equazione ammette due soluzioni reali e distinte (determinata).
Perché dobbiamo aggiungere un segno ± nell’estrarre la radice quadrata?
Aggiungere il segno ± è necessario poiché entrambe le possibilità risolvono l’equazione. Infatti, se eleviamo al quadrato entrambe le soluzioni otteniamo:
(+√((-c)/(a)))^2 = (-c)/(a) ; (-√((-c)/(a)))^2 = (-c)/(a)
Come richiesto dall’equazione monomia di secondo grado. È importante fare attenzione a non trascurare questo dettaglio e a non confondere l’estrarre la radice quadrata di un numero con la risoluzione di un’equazione, in cui cerchiamo tutti i possibili valori che, sostituiti a x, rendono vera l’uguaglianza.
Esempi di equazioni pure
- -2x^2+4 = 0
Applicando il procedimento, otteniamo:
x^2 = (-4)/(-2) = (4)/(2) = 2
Il secondo membro è positivo, quindi l’equazione ammette due soluzioni distinte date da x_(1,2) = ±√(2). - 3x^2+7 = 0
Si ha:
x^2 = (-7)/(3)
Dove (-7)/(3) è negativo, dunque l’equazione non ammette soluzioni reali.
Fonte del contenuto: Matematika.it
Equazioni di secondo grado spurie
Un’equazione di secondo grado spuria è un’equazione di secondo grado in forma normale in cui il termine noto è nullo mentre il coefficiente del termine di grado 1 non è nullo: b ≠ 0, c = 0
L’equazione di secondo grado spuria può essere scritta come:
ax^2+bx = 0
con a ≠ 0 e b ≠ 0. In questo caso, la risoluzione è immediata e non richiede l’utilizzo della formula del discriminante.
Per risolvere un’equazione di secondo grado spuria, è necessario effettuare un raccoglimento a fattore comune:
ax^2+bx = 0 → x(ax+b) = 0
Successivamente, applichiamo la legge di annullamento del prodotto, ossia poniamo separatamente ognuno dei due fattori uguale a zero:
x = 0 ; ax+b = 0
In questo modo otteniamo due soluzioni distinte:
x1 = 0, x2 = -(b)/(a)
Esempio di equazione di secondo grado spuria
Consideriamo l’equazione:
3x^2+7x = 0
Applicando il procedimento descritto sopra, otteniamo:
x(3x+7) = 0
Le soluzioni dell’equazione sono quindi:
x = 0 ; 3x+7 = 0 → x = -(7)/(3)
Metodo alternativo – Risolvere le equazioni di secondo grado per scomposizione
Introduzione
Esiste un metodo alternativo per risolvere le equazioni di secondo grado, che non richiede l’utilizzo della formula del delta, ma ha una limitazione pratica. Questo metodo può essere utilizzato per le equazioni complete e non complete.
Scomposizione del polinomio di secondo grado
Consideriamo la forma normale delle equazioni di secondo grado:
ax^2+bx+c = 0 con a ≠ 0
Se è possibile scomporre il polinomio di secondo grado come prodotto di due binomi di grado 1, allora possiamo scomporre il polinomio nella seguente forma:
ax^2+bx+c = a(x+A)(x+B)
Calcolo delle soluzioni
Riscriviamo l’equazione nella forma equivalente:
a(x+A)(x+B) = 0 → (x+A)(x+B) = 0
Applichiamo la legge di annullamento del prodotto per calcolare le soluzioni:
x+A = 0 → x = -A ; x+B = 0 → x = -B
Questo metodo può essere utilizzato solo per le equazioni di secondo grado determinate, cioè con due soluzioni reali distinte (x_1 = -A ≠-B = x_2) o con due soluzioni reali coincidenti (A = B).
Tecniche di scomposizione
Per ottenere la scomposizione del polinomio di grado 2 possiamo usare qualsiasi tecnica atta allo scopo, come la differenza di quadrati, il trinomio notevole con somma e prodotto, il quadrato di binomio, e altre tecniche.
Metodo di scomposizione del trinomio di secondo grado
Il metodo di scomposizione del trinomio di secondo grado è utile per diversi motivi. In primo luogo, talvolta è possibile riconoscere al volo che il trinomio ax2+bx+c può essere scomposto facilmente, evitando i calcoli della formula del discriminante. In secondo luogo, questo metodo consente di comprendere, dal punto di vista teorico, perché nelle equazioni di secondo grado con delta uguale a zero si parla di due soluzioni reali e coincidenti, o anche di una soluzione reale con molteplicità algebrica 2.
Supponiamo di avere l’equazione di secondo grado x2+4x+4 = 0. È evidente che il primo membro può essere scritto come il quadrato di un binomio, ovvero (x+2)2. Possiamo scrivere l’equazione come (x+2)(x+2) = 0. Pertanto, x = -2 è una duplice soluzione dell’equazione, poiché annulla sia il primo fattore sia il secondo. Questo significa che x = -2 è un singolo valore numerico che risolve l’equazione in due modi, ovvero rappresenta una soluzione reale con molteplicità algebrica 2.
Inoltre, il metodo di scomposizione del trinomio di secondo grado può essere utilizzato al contrario per scomporre polinomi in cui i prodotti notevoli non sono d’aiuto. Supponiamo di avere un polinomio di secondo grado ax2+bx+c e di volerlo scomporre. Possiamo considerare l’equazione di secondo grado associata ax2+bx+c = 0. Se l’equazione ha soluzioni reali, allora il polinomio può essere scomposto nel prodotto di due binomi.
- Se Δ = 0, l’equazione ammette un’unica soluzione con molteplicità algebrica 2. In questo caso, la scomposizione del polinomio è data da ax2+bx+c = a(x-x1)2, dove x1 è la soluzione unica dell’equazione.
- Se Δ > 0, l’equazione ammette due soluzioni reali distinte x1 e x2. In questo caso, la scomposizione del polinomio è data da ax2+bx+c = a(x-x1)(x-x2).
In entrambi i casi, è importante ricordare di anteporre un segno meno alle soluzioni.
Stai guardando: EQUAZIONI DI SECONDO GRADO