TANGENTE E COTANGENTE
La tangente e la cotangente, rappresentate rispettivamente come tan(α) e cot(α), sono funzioni trigonometriche che si definiscono sulla circonferenza goniometrica utilizzando il seno e il coseno di un angolo. Tali funzioni assegnano un valore reale ad ogni angolo. In questa lezione, discuteremo dettagliatamente della tangente e della cotangente di un angolo, partendo dalle definizioni e spiegando le loro proprietà.

Successivamente, presenteremo i grafici di queste due funzioni goniometriche. Le definizioni di tangente e cotangente saranno date a partire dalla circonferenza goniometrica, e attraverso l’utilizzo degli aspetti grafici e geometrici delle definizioni, dedurremo l’espressione analitica di queste funzioni in termini di seno e coseno. Non verranno presentati duplicati nelle informazioni per garantire una trattazione dettagliata.
Rappresentazione e definizione di tangente e cotangente
Definizione di tangente di un angolo
La tangente di un angolo α è definita come l’ordinata del punto di intersezione tra la retta tangente alla circonferenza goniometrica nel punto (1,0) e il secondo lato dell’angolo (o il suo prolungamento). Se il secondo lato dell’angolo cade nel primo o nel quarto quadrante, allora è proprio il secondo lato dell’angolo ad intersecare la retta tangente. Se invece il secondo lato dell’angolo giace nel secondo o nel terzo quadrante, sarà il suo prolungamento ad incontrare la retta tangente.
In formule, si ha:
tan(α) = y_T
dove T è il punto di intersezione tra la retta tangente e il secondo lato dell’angolo (o il suo prolungamento).
Tuttavia, se il secondo lato dell’angolo cade sull’asse y, ovvero se α=90° oppure α=270°, tale lato sarà parallelo alla retta tangente e non vi sarà alcun punto di intersezione. Pertanto, per questi valori di α non è definito alcun valore della tangente.
Definizione di tangente con seno e coseno
Definizione di tangente di un angolo con seno e coseno
La tangente di un angolo α (con α≠90° e α≠270°) può essere definita come il rapporto tra il seno e il coseno dello stesso angolo, ovvero:
tan(α) = (sin(α))/(cos(α)), per ogni α ≠ 90°+k180°, k∈Z
Per capire la derivazione di questa relazione, si disegna un angolo α sulla circonferenza goniometrica e si considera la retta tangente alla circonferenza nel punto S(1,0). Si indica con P il punto di intersezione tra il secondo lato dell’angolo e la circonferenza, e con T il punto di intersezione tra il secondo lato dell’angolo e la retta tangente t. Infine, si indicano con Q ed R le proiezioni del punto P sugli assi coordinati.
Considerando i triangoli ORP e OST, si nota che sono simili e hanno i tre angoli uguali: l’angolo α è in comune, entrambi sono triangoli rettangoli e la somma degli angoli interni di un triangolo è 180°. In particolare, i lati di triangoli simili sono ordinatamente in proporzione, quindi vale la relazione:
(TS)/(OS) = (PR)/(OR)
Osservando che OS è un raggio della circonferenza e ricordando che la circonferenza ha raggio unitario, si ha:
(tan(α))/(1) = (sin(α))/(cos(α))
e quindi:
tan(α) = (sin(α))/(cos(α))
che rappresenta la definizione di tangente con seno e coseno.
Seno, Coseno e Tangente : funzioni goniometriche 😉 – YouTube
Definizione di cotangente di un angolo
Definizione di cotangente di un angolo sulla circonferenza goniometrica
La cotangente di un angolo α sulla circonferenza goniometrica può essere definita come l’ascissa del punto di intersezione tra la retta tangente alla circonferenza nel punto A(0,1) e il secondo lato dell’angolo (o il suo prolungamento). Se il secondo lato dell’angolo cade nel primo o nel secondo quadrante (0<α<180°), allora è il secondo lato dell’angolo ad intersecare la retta tangente. Se invece il secondo lato dell’angolo giace nel terzo o nel quarto quadrante (180°<α<360°), sarà il suo prolungamento ad incontrare la retta tangente.
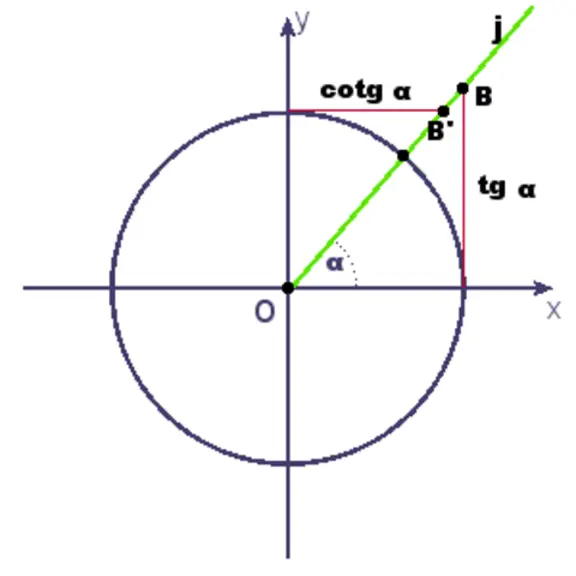
In formule, si ha:
cot(α) = x_C
dove C è il punto di intersezione tra il secondo lato dell’angolo (o il suo prolungamento) e la retta tangente la circonferenza nel punto (0,1).
Tuttavia, se il secondo lato dell’angolo cade sull’asse x, ovvero se α=0°=360° oppure α=180°, non vi sarà alcun punto di intersezione tra la retta c ed il secondo lato dell’angolo. Pertanto, per questi valori di α non è definito alcun valore della cotangente.
Definizione di cotangente con seno e coseno
Definizione di cotangente di un angolo con seno e coseno
La cotangente di un angolo α (con α≠k180°, k∈Z) può essere definita come il rapporto tra il coseno e il seno dello stesso angolo, ovvero:
cot(α) = (cos(α))/(sin(α))
Per dimostrare questa relazione, si disegna un angolo α sulla circonferenza goniometrica, con α≠180° e α≠360°, e si considera la retta tangente alla circonferenza nel punto A(0,1). Si indica con P il punto di intersezione tra il secondo lato dell’angolo e la circonferenza, con C il punto di intersezione tra il secondo lato dell’angolo e la retta tangente c, e con Q ed R le proiezioni del punto P sugli assi y ed x.
Considerando i triangoli rettangoli OAC e OQP, si nota che sono simili e hanno tutti e tre gli angoli congruenti. Pertanto, si può scrivere la proporzione tra i lati omologhi:
(AC)/(OA) = (QP)/(OQ)
Sostituendo i valori delle lunghezze dei lati corrispondenti, si ottiene:
cot(α) = (cos(α))/(sin(α))
che rappresenta la definizione di cotangente con seno e coseno.
Fonte: YouMath.it
Principali valori di tangente e cotangente
Calcolo dei valori di tangente e cotangente
Non è necessario memorizzare i valori notevoli di tangente e cotangente. Infatti, grazie alle definizioni che abbiamo dato in precedenza:
tan(α) = (sin(α))/(cos(α))
cot(α) = (cos(α))/(sin(α))
è possibile ricavare i valori di tangente e cotangente degli angoli notevoli conoscendo i valori del seno e del coseno in corrispondenza di tali angoli.
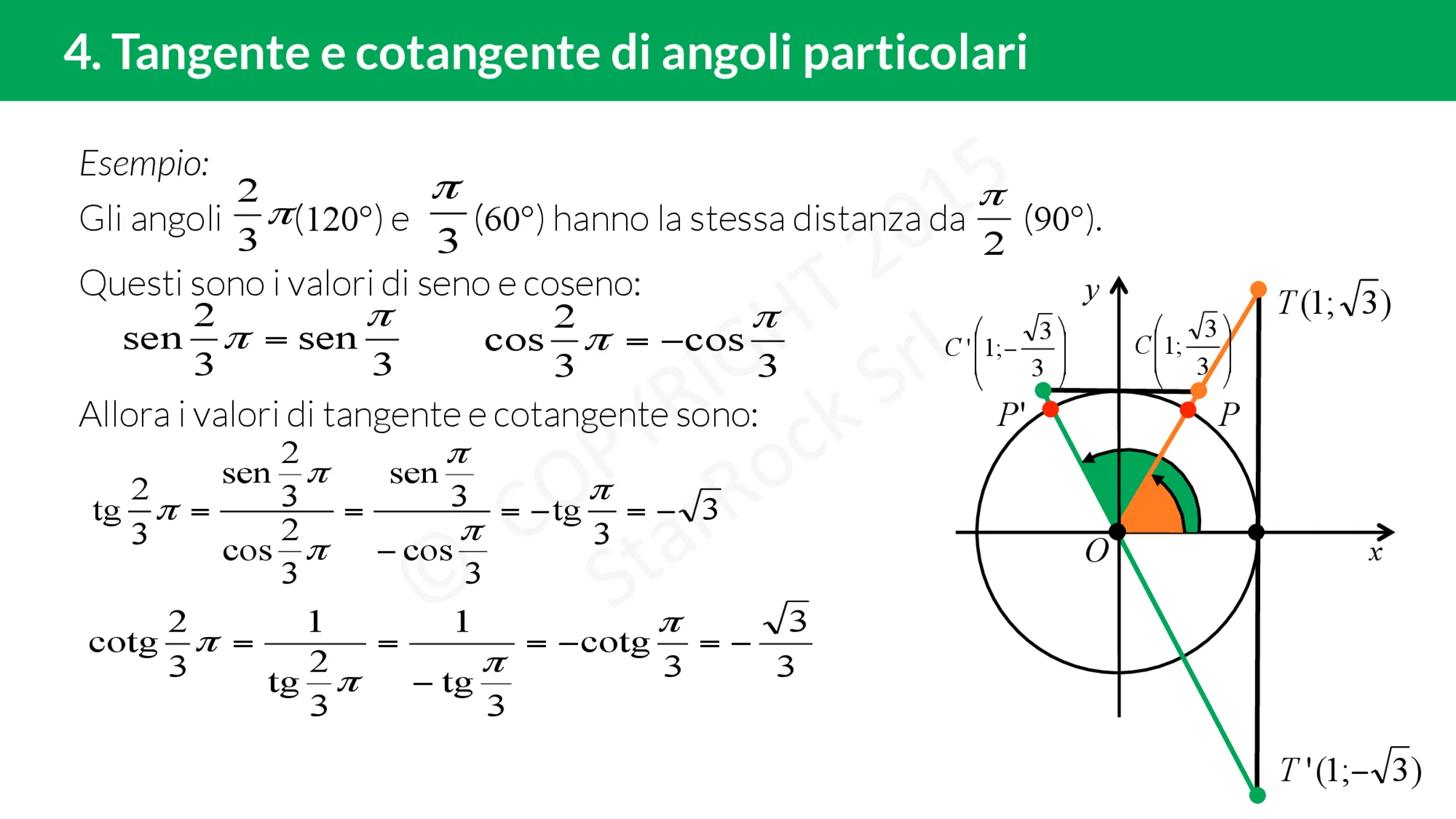
Ad esempio, se α=π/6, sapendo che il seno di 30° vale 1/2 e che il coseno di 30° vale √3/2, è possibile ricavare immediatamente il valore della tangente e della cotangente di 30°:
tan((π)/(6)) = tan(30°) = (sin(30°))/(cos(30°)) = ((1)/(2))/((√(3))/(2)) = (1)/(2)·(2)/(√(3)) = (1)/(√(3)) = (√(3))/(3)
cot((π)/(6)) = cot(30°) = (cos(30°))/(sin(30°)) = ((√(3))/(2))/((1)/(2)) = (√(3))/(2)·2 = √(3)
Tabella dei valori notevoli
Nella seguente tabella sono riportati i valori di seno, coseno, tangente e cotangente per i principali angoli espressi sia in gradi che in radianti:
Rappresentazione e definizione di tangente e cotangente
Partiamo dalla definizione di tangente e cotangente e come prima cosa disegniamo un angolo α sulla circonferenza goniometrica facendo coincidere il vertice dell’angolo col centro della circonferenza ed il suo primo lato col semiasse positivo delle ascisse:
Definizione di tangente di un angolo
Dato un angolo α sulla circonferenza goniometrica consideriamo la retta t tangente la circonferenza nel punto S(1,0) e sia T il punto di intersezione tra tale retta ed il secondo lato dell’angolo (o il suo prolungamento).
Si definisce tangente dell’angolo α l’ordinata del punto T dato dall’intersezione tra il secondo lato dell’angolo (o il suo prolungamento) e la retta tangente la circonferenza nel punto (1,0). In formule: tan(α) = yT.
Definizione di cotangente di un angolo
Consideriamo un angolo α sulla circonferenza goniometrica e la retta c tangente la circonferenza nel punto A(0,1). Sia C il punto di intersezione tra tale retta ed il secondo lato dell’angolo (o il suo prolungamento).
Si definisce cotangente dell’angolo α l’ascissa del punto C dato dall’intersezione tra il secondo lato dell’angolo (o il suo prolungamento) e la retta tangente la circonferenza nel punto (0,1), ossia cot(α) = xC.
Definizione di tangente con seno e coseno
La tangente di un angolo α è il rapporto tra il seno ed il coseno dello stesso angolo, ossia tan(α) = (sin(α))/(cos(α)), per ogni α ≠ 90°+k180°, k∈Z.
Definizione di cotangente con seno e coseno
La cotangente di un angolo α è il rapporto tra il coseno ed il seno dello stesso angolo, ossia cot(α) = (cos(α))/(sin(α)), per ogni α ≠ k180°, k∈Z.
Principali valori di tangente e cotangente
Non è necessario ricordare a memoria i valori notevoli di tangente e cotangente, ma grazie alle definizioni di tangente e cotangente è possibile ricavare tali valori conoscendo il valore del seno e del coseno in corrispondenza di tali angoli.
| α in gradi | α in radianti | sin(α) | cos(α) | tan(α) | cot(α) |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | not ∃ |
| 30° | (π)/(6) | (1)/(2) | (√(3))/(2) | (√(3))/(3) | √(3) |
| 45° | (π)/(4) | (√(2))/(2) | (√(2))/(2) | 1 | 1 |
| 60° | (π)/(3) | (√(3))/(2) | (1)/(2) | √(3) | (√(3))/(3) |
| 90° | (π)/(2) |
Le funzioni tangente e cotangente
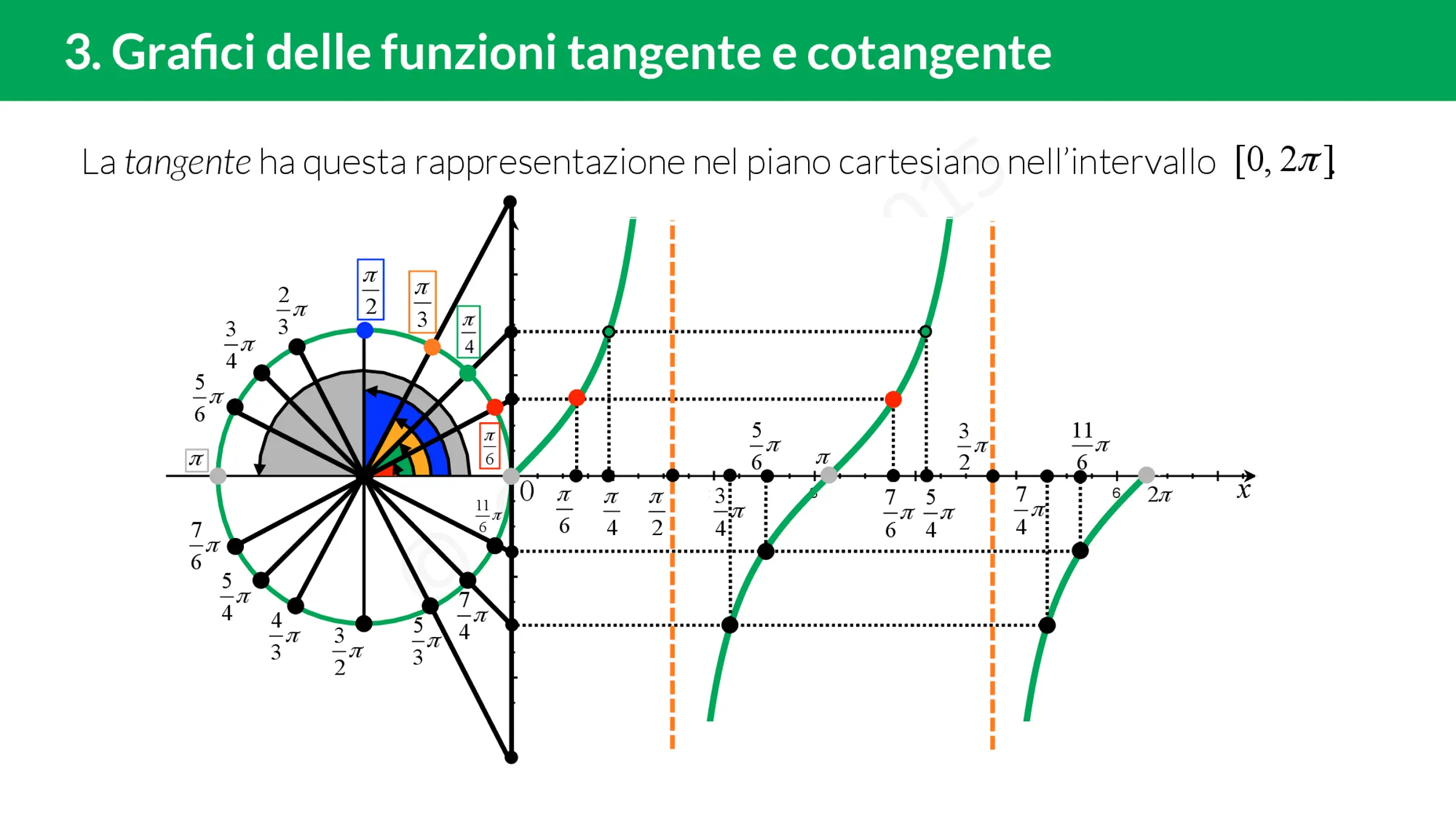
Per tracciare il grafico delle funzioni tangente e cotangente, è necessario riepilogare alcune informazioni essenziali.
Il dominio e l’immagine delle funzioni
La funzione tangente non è definita per α = (π)/(2)+kπ, il che significa che il suo dominio è:
Dom[tan] = R-(π)/(2)+kπ, k ∈ Z
Allo stesso modo, la funzione cotangente non è definita per α = kπ, il che significa che il suo dominio è:
Dom[cot] = R-kπ, k ∈ Z
Entrambe le funzioni hanno come immagine l’insieme R dei numeri reali.
I limiti delle funzioni
Chi ha già confidenza con i limiti saprà che:
lim_(x → ((π)/(2))^+) tan(x) = -∞
lim_(x → ((π)/(2))^-) tan(x) = +∞
lim_(x → 0^+) cot(x) = +∞
lim_(x → 0^-) cot(x) = -∞
La periodicità delle funzioni
Fissato un angolo α compreso tra 0 e 2π, se a tale angolo sommiamo o sottraiamo π otterremo un nuovo angolo la cui tangente e cotangente coincidono con quella dell’angolo α. In simboli:
tan(α) = tan(α+kπ) per qualsiasi k ∈ Z
cot(α) = cot(α+kπ) per qualsiasi k ∈ Z
Da qui deduciamo che le funzioni tangente e cotangente sono funzioni periodiche di periodo π.
Consultando il grafico delle funzioni tangente e cotangente, è possibile riconoscere tutte le proprietà elencate a partire dalla definizione.
| α in gradi | α in radianti | sin(α) | cos(α) | tan(α) |
|---|
Stai guardando: TANGENTE E COTANGENTE