PARALLELOGRAMMA
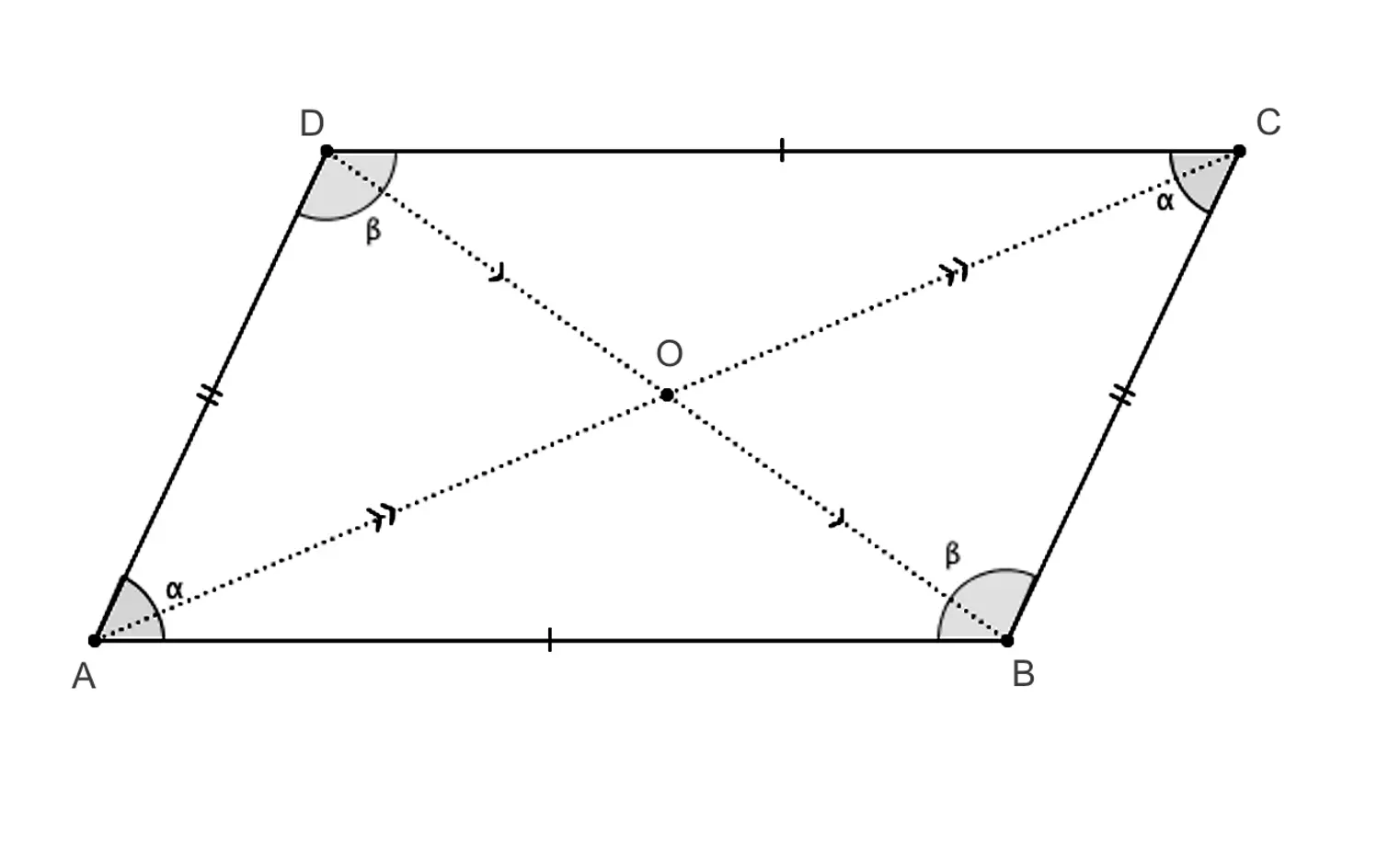
In Geometria, un parallelogramma è un poligono convesso che presenta quattro lati paralleli a due a due. Una definizione alternativa di parallelogramma è quella di un quadrilatero convesso con i lati opposti paralleli e quindi con i lati opposti congruenti. Per maggiori informazioni sul parallelogramma, in questo formulario troverete una sintesi completa che include la definizione, le formule e le proprietà geometriche che lo caratterizzano.

Definizione di parallelogramma
Un parallelogramma è un quadrilatero convesso in cui i lati opposti sono paralleli. Ciò significa che se tracciamo una linea che attraversa il parallelogramma, questa taglierà i lati paralleli in modo uguale.
Definizione equivalente di parallelogramma
Esistono diverse definizioni equivalenti di parallelogramma, ma tutte sottolineano la stessa caratteristica fondamentale: i lati opposti sono paralleli. Ad esempio, un parallelogramma può essere definito come un quadrilatero con due coppie di lati paralleli o come un quadrilatero in cui le diagonali si dividono a metà.
Altre informazioni utili
È importante ricordare che un quadrilatero ha quattro lati, mentre il termine “convesso” significa che non ci sono prolungamenti dei lati e che i lati non si intrecciano tra di loro. Questi concetti sono fondamentali per definire correttamente un parallelogramma.
Fonte: Wikipedia
Formule del parallelogramma
Definizione delle variabili

Nelle formule del parallelogramma, consideriamo b come il lato di base, L come il lato obliquo e h come l’altezza. Inoltre, chiamiamo d1 e d2 rispettivamente la diagonale minore e la diagonale maggiore, 2p il perimetro e A l’area del parallelogramma.
Il parallelogramma – YouTube
Formule del parallelogramma
Le formule del parallelogramma sono utili per calcolare il perimetro, l’area, la base e l’altezza del parallelogramma. Ecco le principali formule:
- Perimetro: 2p = 2L + 2b
- Base: b = (2p – 2L) / 2
- Lato obliquo: L = (2p – 2b) / 2
- Area: A = b × h
- Base: b = A / h
- Altezza: h = A / b
Proprietà del parallelogramma
Il parallelogramma ha numerose proprietà, tra cui:
- I lati opposti sono paralleli.
- I lati opposti sono congruenti.
- Gli angoli opposti sono congruenti, gli angoli consecutivi sono supplementari.
- La somma degli angoli interni di un parallelogramma è uguale a un angolo giro.
- Le diagonali si intersecano nel loro punto medio.
- Ciascuna diagonale divide il parallelogramma in due triangoli congruenti.
- Il punto di intersezione tra le due diagonali è il centro di simmetria del parallelogramma.
- Il parallelogramma è un caso particolare di trapezio in cui i lati sono a due a due paralleli.
Insieme dei parallelogrammi
Il parallelogramma è uno dei tipi di quadrilateri convessi. Esiste una classificazione con un diagramma di Eulero-Venn nell’insieme dei quadrilateri convessi.
Tipi di parallelogramma particolari
Ci sono tre tipi di parallelogramma particolari:
- Il rombo è un parallelogramma con i lati congruenti.
- Il rettangolo è un parallelogramma con gli angoli congruenti (90°).
- Il quadrato è un parallelogramma con i lati congruenti e gli angoli congruenti (90°).
Stai guardando: PARALLELOGRAMMA