DISTANZA TRA DUE PUNTI
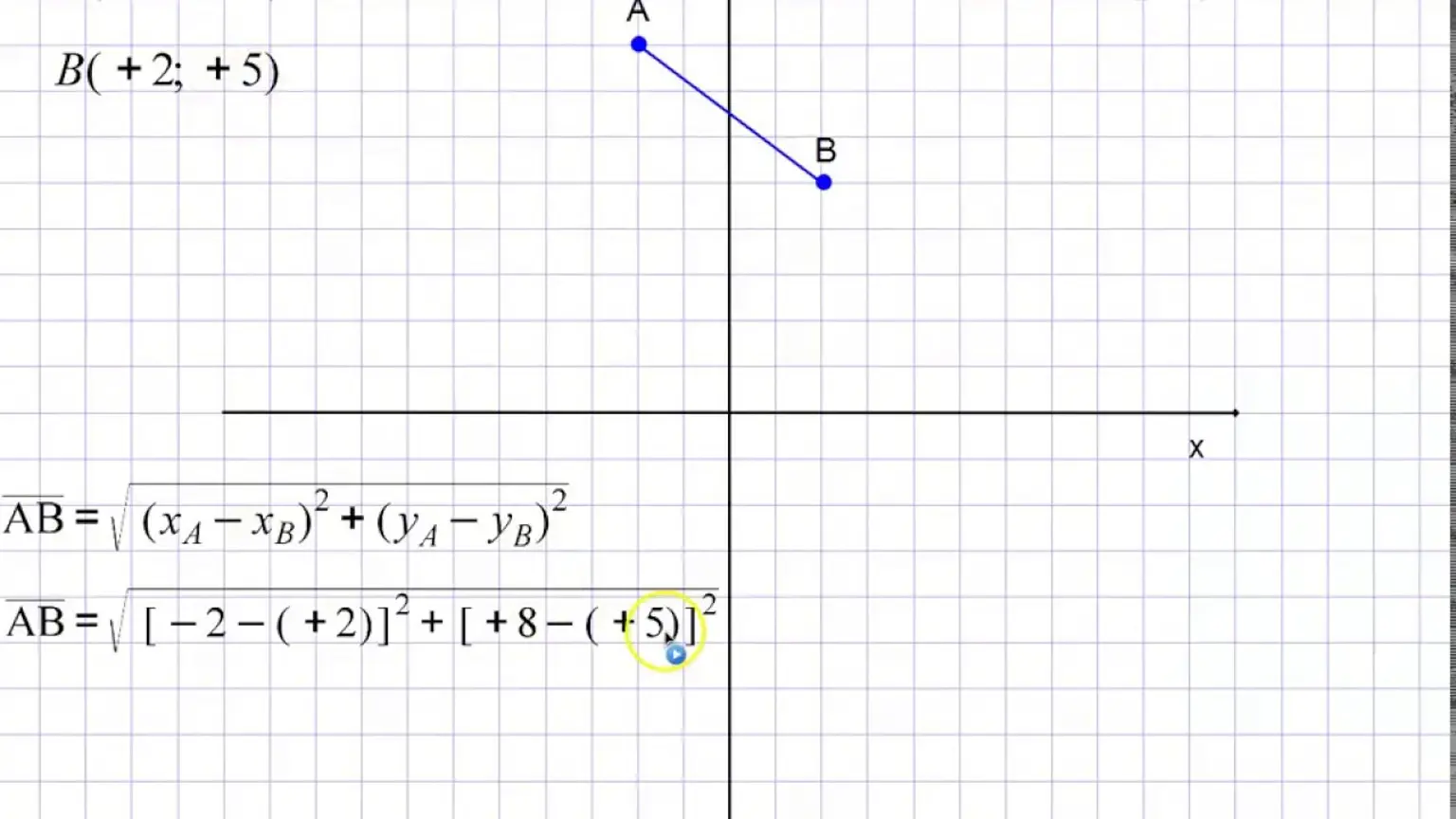
La distanza tra due punti nel piano cartesiano, anche chiamata distanza euclidea, è definita come la radice quadrata della somma dei quadrati delle differenze tra le ascisse e le ordinate dei due punti. Essendo la distanza tra due punti definita come non negativa, sarà positiva se i due punti sono distinti, oppure nulla se i due punti coincidono. La formula della distanza tra due punti nel piano cartesiano può essere utilizzata per calcolare la distanza tra due punti in un sistema di coordinate cartesiane.

Inoltre, la dimostrazione della formula può essere fornita tramite il teorema di Pitagora, e può essere contestualizzata nel caso particolare di una coppia di punti allineati orizzontalmente o verticalmente. Infine, per aiutare nella comprensione e nella risoluzione degli esercizi, forniremo alcuni esempi di calcolo. Potrete trovare una serie di esercizi correlati e un comodo strumento di calcolo online alla fine della pagina.
Formula della distanza tra due punti
La formula per calcolare la distanza tra due punti nel piano cartesiano, individuati da una coppia di coordinate cartesiane (ascissa, ordinata), è la distanza euclidea.
Definizione
Definiamo la distanza euclidea tra i due punti P1 e P2 come d(P1,P2) o P1P2, il valore dato da:
d(P1,P2) = √((x2-x1)2+(y2-y1)2)
A parole: la distanza tra due punti del piano è la radice quadrata della somma tra il quadrato della differenza delle ascisse e il quadrato della differenza delle ordinate dei due punti.
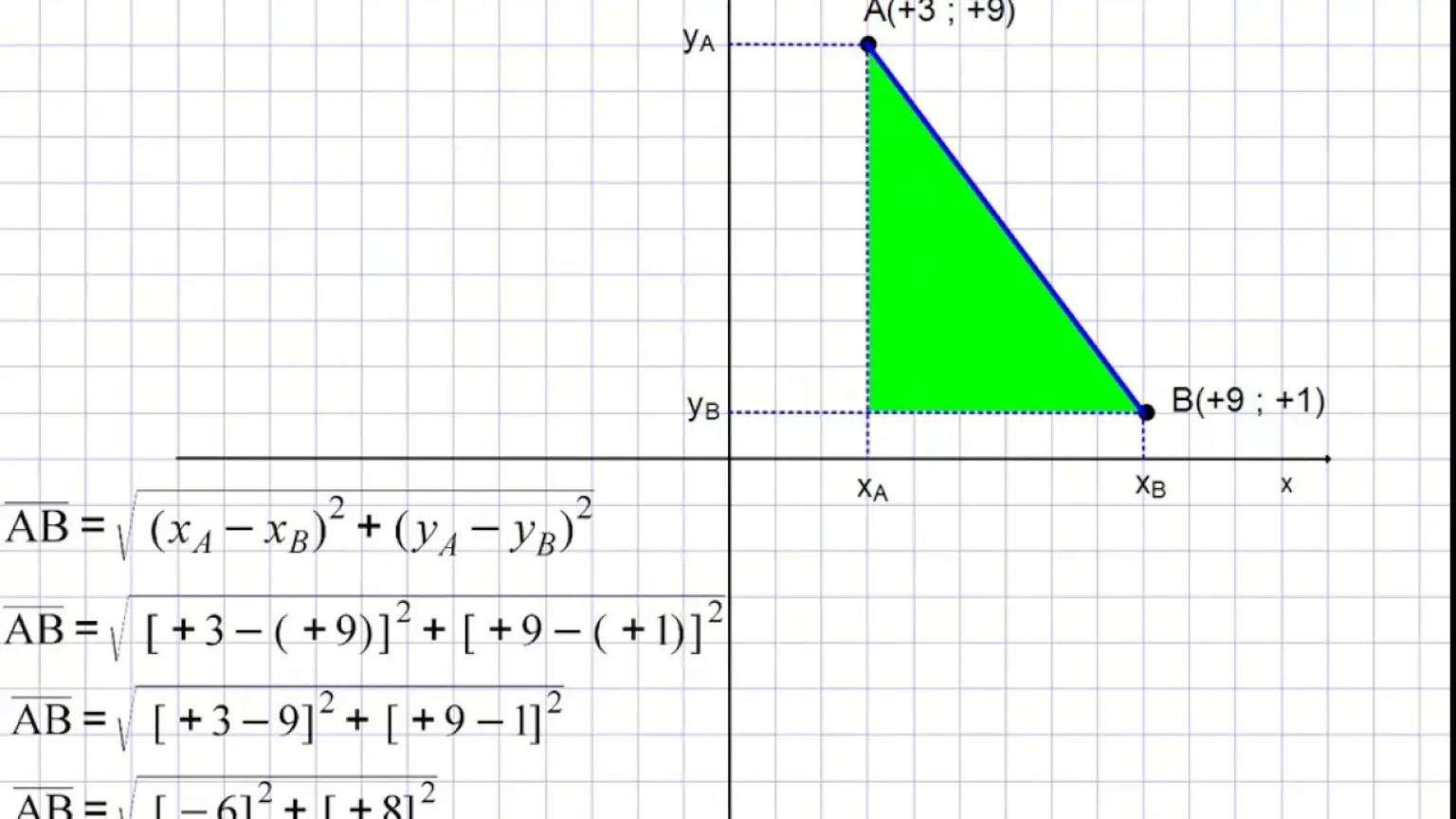
Fonte: Wikipedia
Esempi sulla distanza tra due punti
Calcolo della distanza tra due punti sul piano cartesiano. – YouTube
Esempio A
Calcoliamo la distanza tra i punti P1 = (1,2) e P2 = (3,4):
d(P1,P2) = √((x2-x1)2+(y2-y1)2) = √((3-1)2+(4-2)2) = √(22+22) = √8
La distanza è quindi pari alla radice di 8, che può essere riscritta come 2√2.
Esempio B
Calcoliamo la distanza tra i punti P = (1,-2) e Q = (2,2):
d(P,Q) = √((xQ-xP)2+(yQ-yP)2) = √((2-1)2+(2-(-2))2) = √(12+42) = √17
È importante prestare attenzione ai segni quando si applica la formula della distanza tra due punti.
Esempio C
Calcoliamo la distanza del punto C = (5,12) dall’origine degli assi:
d(O,C) = √((xC-xO)2+(yC-yO)2) = √((5-0)2+(12-0)2) = √(25+144) = √169 = 13
La distanza è 13, che corrisponde alla radice di 169.
Esempio D
Determiniamo la distanza tra i punti A = (-1,-3) e B = (5,-3):

d(A,B) = √((xB-xA)2+(yB-yA)2) = √((5-(-1))2+(-3-(-3))2) = √(36+0) = √36 = 6
Casi particolari nel calcolo della distanza tra due punti
1. Distanza tra due punti allineati su una retta orizzontale
Se i due punti sono allineati su una retta orizzontale del tipo y = a, cioè parallela all’asse delle ascisse, allora le loro coordinate devono essere della forma P1 = (x1,a) e P2 = (x2,a). La formula della distanza tra i due punti si semplifica in:
d(P1,P2) = |x2-x1|
Il valore assoluto è necessario perché la differenza x2-x1 potrebbe essere negativa.
2. Distanza tra due punti allineati su una retta verticale
Se i due punti sono allineati su una retta verticale del tipo x = a, cioè parallela all’asse delle ordinate, allora le loro coordinate devono essere della forma P1 = (a,y1) e P2 = (a,y2). La formula della distanza tra i due punti si semplifica in:
d(P1,P2) = |y2-y1|
3. Distanza di un punto dall’origine degli assi
Per calcolare la distanza di un punto P = (xP,yP) dall’origine degli assi O = (0,0), si applica la formula generale per la distanza tra due punti, tenendo conto che uno dei due punti è l’origine:
d(P,O) = √(xP2+yP2)
Dimostrazione della formula per la distanza tra due punti nel piano
Per dimostrare la formula per la distanza tra due punti nel piano, consideriamo un terzo punto C allineato orizzontalmente a P1 e verticalmente a P2:
C = (xC,yC) = (x2,y1)
Il triangolo P1P2C è un triangolo rettangolo in C, poiché è allineato orizzontalmente a P1 e verticalmente a P2.
Applicando il teorema di Pitagora, possiamo calcolare la distanza P1P2 come lunghezza dell’ipotenusa del triangolo rettangolo P1P2C con angolo retto in C:
P1P2 = √(P1C2+CP22)
Scriviamo le lunghezze dei due cateti come semplici differenze. Per P1C come differenza tra le ascisse dei due punti:
P1C = |xC-x1| = |x2-x1|
E per CP2 come differenza tra le ordinate dei due punti:
CP2 = |y2-yC| = |y2-y1|
Sostituendo il tutto nella formula del teorema di Pitagora, ricaviamo:
P1P2 = √((|x2-x1|)2+(|y2-y1|)2)
Eliminiamo il valore assoluto, poiché abbiamo un elevamento al quadrato:
P1P2 = √((x2-x1)2+(y2-y1)2)
La formula per la distanza tra due punti è dimostrata.
Fonte: Matematichiamo
Proprietà della distanza tra due punti
La distanza euclidea tra due punti nel piano cartesiano è definita dalla seguente formula:
d(P1, P2) = √((x2 – x1)2 + (y2 – y1)2)
Proprietà della distanza euclidea
Ecco alcune proprietà fondamentali della distanza euclidea:
Proprietà 1: La distanza euclidea è ben definita
Il radicando della formula della distanza è una somma di quadrati e quindi è sempre positivo o nullo (nel caso in cui i due punti coincidano). Ciò significa che la definizione di distanza è ben posta, in quanto non ci troveremo mai a calcolare la radice quadrata di un numero negativo.
Proprietà 2: La distanza euclidea è non negativa
Il valore della distanza euclidea è necessariamente non negativo, in quanto è la radice quadrata di un numero positivo o nullo. In altre parole, la distanza euclidea è sempre maggiore o uguale a zero e sarà zero solo se i due punti coincidono.
Proprietà 3: La distanza euclidea è simmetrica
La distanza euclidea non dipende dall’ordine dei punti tra cui si calcola, cioè:
d(P1, P2) = d(P2, P1)
In altre parole, la distanza euclidea è simmetrica.
Proprietà 4: La distanza euclidea soddisfa la proprietà di disuguaglianza triangolare
La distanza euclidea tra due punti soddisfa la proprietà di disuguaglianza triangolare, che afferma che la lunghezza di un lato di un triangolo è sempre minore della somma delle lunghezze degli altri due lati. In altre parole:
d(P1, P2) ≤ d(P1, P3) + d(P3, P2)
d(P2, P3) ≤ d(P2, P1) + d(P1, P3)
d(P3, P1) ≤ d(P3, P2) + d(P2, P1)
La disuguaglianza triangolare è importante in molti contesti
Distanza tra due punti nello spazio e in più dimensioni
L’approfondimento della distanza euclidea tra due punti nel piano si generalizza facilmente in spazi vettoriali n-dimensionali. Per la distanza tra due punti nello spazio, si definiscono i punti P1 e P2 con le coordinate (x1,y1,z1) e (x2,y2,z2) rispettivamente. La formula della distanza euclidea diventa quindi:
d(P1,P2) = √((x2-x1)2+(y2-y1)2+(z2-z1)2)
In uno spazio vettoriale ad n dimensioni Rn (n ≥ 1), la distanza euclidea tra due punti P1 e P2 con le coordinate (c1,…,cn) e (d1,…,dn) rispettivamente, può essere espressa come:
d(P1,P2) = ||P2-P1||
dove ||·|| indica la norma di un vettore. Esplicitamente, la formula della distanza euclidea diventa:
d(P1,P2) = √((d1-c1)2+(d2-c2)2+…+(dn-cn)2)
Questa formula può anche essere espressa usando il simbolo di sommatoria:
d(P1,P2) = √(Σi = 1n(di-ci)2)
Per maggiori dettagli sull’argomento si può consultare la lezione dedicata al concetto di spazio euclideo.
Stai guardando: DISTANZA TRA DUE PUNTI