FUNZIONE PARI, FUNZIONE DISPARI

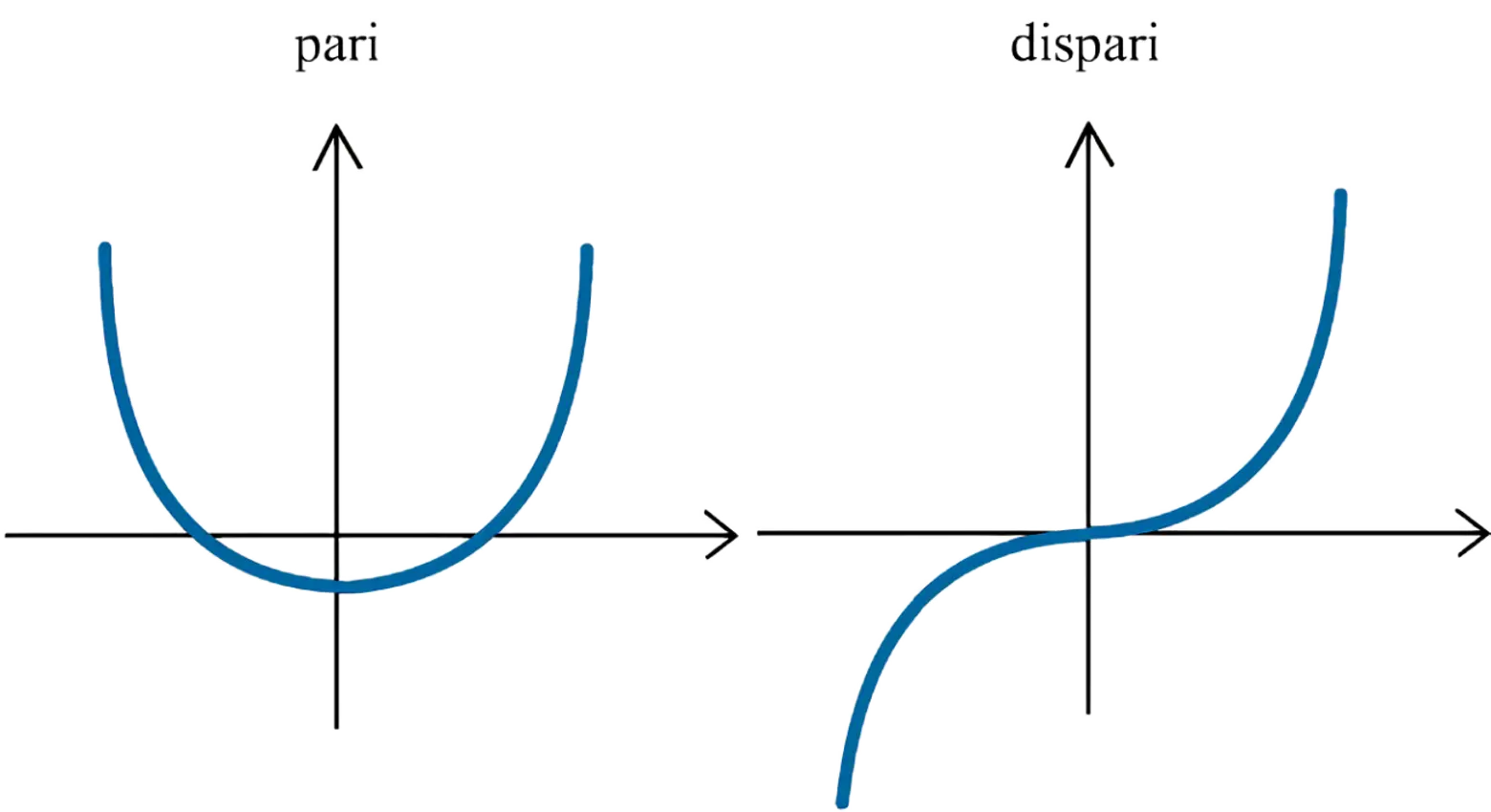
Una funzione è considerata pari se è simmetrica rispetto all’asse delle ordinate, il che significa che il valore della funzione per x e -x è lo stesso. Al contrario, una funzione è considerata dispari se è simmetrica rispetto all’origine, il che significa che il valore della funzione per x e -x è opposto in segno. Questi termini potrebbero sembrare poco intuitivi, ma seguendo le rispettive definizioni è possibile determinare se una funzione è pari, dispari o nessuna delle due.

Definizioni di funzione pari e dispari
Per introdurre le definizioni di parità e disparità di una funzione non possiamo prescindere dal concetto di simmetria di un insieme reale rispetto allo zero. Consideriamo una funzione
f:Dom(f) ⊆ R → R
e immaginiamo di rappresentare il dominio Dom(f) su una retta orientata, avendo cura di indicare il valore x = 0. Se si ricorda cos’è la simmetria rispetto a un punto, si capisce in un istante qual è la proprietà che caratterizza un insieme reale simmetrico rispetto all’origine (il valore zero).
Funzione pari
Una funzione f:Dom(f) ⊆ R → R è una funzione pari se il suo dominio è simmetrico rispetto all’origine e se vale la proprietà:
f(-x) = f(x) ∀ x∈ Dom(f)
Funzione dispari
Una funzione f:Dom(f) ⊆ R → R è una funzione dispari se il suo dominio è simmetrico rispetto all’origine e se soddisfa la proprietà:
f(-x) = -f(x) ∀ x∈ Dom(f)
Simmetrie e Periodicità : Funzioni Pari – Funzioni Dispari – Funzioni Periodiche – YouTube
Funzione non pari e non dispari
Nel caso in cui non sussistano alcune delle precedenti condizioni, la funzione considerata non è né pari né dispari.
Al di là delle condizioni algebriche che contraddistinguono le funzioni pari e le funzioni dispari, è importante ricordare che le definizioni di parità e disparità non possono prescindere dalla simmetria del dominio rispetto all’origine. Per questo motivo la prima ipotesi che si dovrà verificare sarà proprio quella relativa alla simmetria del dominio: se essa sussiste, si procederà con il controllo della condizione algebrica, in caso contrario si concluderà che la funzione in esame non è né pari né dispari.
DominioSimmetrico → Cond. algebrica
begincases
f(-x) = f(x) → Pari ;
f(-x) = -f(x) → Dispari ;
Altrimenti → Niente ;
Non simmetrico → Niente
endcases
Fonte: youmath.it
Esempi di funzioni pari e dispari
Applichiamo le definizioni in alcuni esempi per stabilire se le funzioni proposte sono pari o dispari.
Esempio I
Consideriamo
f(x) = x^4+3x^2
La funzione è pari, infatti è definita su tutto R che è un insieme evidentemente simmetrico rispetto all’origine, e inoltre:
f(-x) = (-x)^4+3(-x)^2 = x^4+3x^2 = f(x)
Non è dispari, infatti:
f(-x) = (-x)^4+3(-x)^2 = x^4+3x^2 = f(x) ; e ;-f(x) = -(x^4+3x^2) = -x^4-3x^2
Quindi f(-x) ≠-f(x).
Si noti che nella verifica della condizione algebrica abbiamo effettuato la valutazione della funzione sostituendo -x in luogo di x. Onde evitare banali errori di distrazioni si consiglia di ricorrere alle parentesi e di scrivere meccanicamente (-x) in luogo di x.
Esempio II
Sia
f(x) = 2x^7+3x^5+4x
Anche in questo caso abbiamo a che fare con una funzione polinomiale, pertanto definita su Dom(f) = R, quindi ha senso procedere con il controllo delle condizioni algebriche che definiscono la parità e la disparità.
La funzione non è pari, poiché:
f(-x) = 2(-x)^7+3(-x)^5+4(-x) = -2x^7-3x^5-4x ≠ f(x)
È dispari, infatti:
f(-x) = 2(-x)^7+3(-x)^5+4(-x) = -2x^7-3x^5-4x = -(2x^7+3x^5+4x) = -f(x)
Esempio III
La funzione
f(x) = x^7+x^6+2x^4+3x
è definita su tutto R, per cui possiamo procedere con la verifica della condizione algebrica.
Non è pari, perché:
f(-x) = (-x)^7+(-x)^6+2(-x)^4+3(-x) = -x^7+x^6+2x^4-3x ≠ f(x)
Non è dispari, infatti:
f(-x) = (-x)^7+(-x)^6+2(-x)^4+3(-x) = ;-x^
Proprietà delle funzioni pari e dispari
Dopo aver fornito le definizioni di funzione pari e di funzione dispari, procediamo con l’elenco delle proprietà più importanti di cui esse godono, e omettiamo le dimostrazioni.
Non sottovalutiamo queste proprietà perché possono tornare davvero utili nel prosieguo dello studio dell’Analisi matematica. Possono semplificare notevolmente lo studio di una funzione o ancora il calcolo di un integrale.
Qui di seguito considereremo due funzioni entrambe definite su un insieme simmetrico rispetto all’origine D ⊆ R:
f : D ⊆ R → R ; g : D ⊆ R → R
Parità e disparità della funzione nulla
f(x) è una funzione pari che dispari su D se e solo se f(x) è identicamente nulla su D.
Operazioni con le funzioni pari
In riferimento alle operazioni tra funzioni, se f(x) e g(x) sono funzioni pari su D allora:
- la funzione somma f(x)+g(x) è una funzione pari;
- la funzione differenza f(x)-g(x) è una funzione pari;
- la funzione prodotto f(x)·g(x) è una funzione pari;
- la funzione quoziente (f(x))/(g(x)) con g(x) ≠ 0 è una funzione pari.
Indipendentemente dal valore della costante reale non nulla c∈R-0, la funzione c·f(x) è una funzione pari. Se c fosse uguale a 0 la funzione sarebbe identicamente nulla ed è dunque sia pari che dispari.
Operazioni con le funzioni dispari
Se f(x) e g(x) sono funzioni dispari su D allora:
- la funzione somma f(x)+g(x) è una funzione dispari;
- la funzione differenza f(x)-g(x) è una funzione dispari;
- la funzione prodotto f(x)·g(x) è una funzione pari;
- la funzione quozione (f(x))/(g(x)) con g(x) ≠ 0 è una funzione pari.
Indipendentemente dal valore della costante reale non nulla c∈R-0, la funzione c·f(x) è una funzione dispari. Se c fosse uguale a 0 allora la funzione sarebbe identicamente nulla che è sia pari che dispari.
Operazioni tra funzioni pari e funzioni dispari
Se f(x) è una funzione pari e g(x) è una funzione dispari su D, entrambe non identicamente nulle, allora:
- la funzione somma f(x)+g(x) non è né pari né dispari;
- la funzione differenza f(x)-g(x) non è né pari né dispari;
- la funzione prodotto f(x)·g(x) è una funzione dispari;
- la funzione quozione (f(x))/(g(x)) con g(x) ≠ 0 è una funzione dispari.
Stai guardando: FUNZIONE PARI, FUNZIONE DISPARI