FUNZIONE ESPONENZIALE E^X, A^X
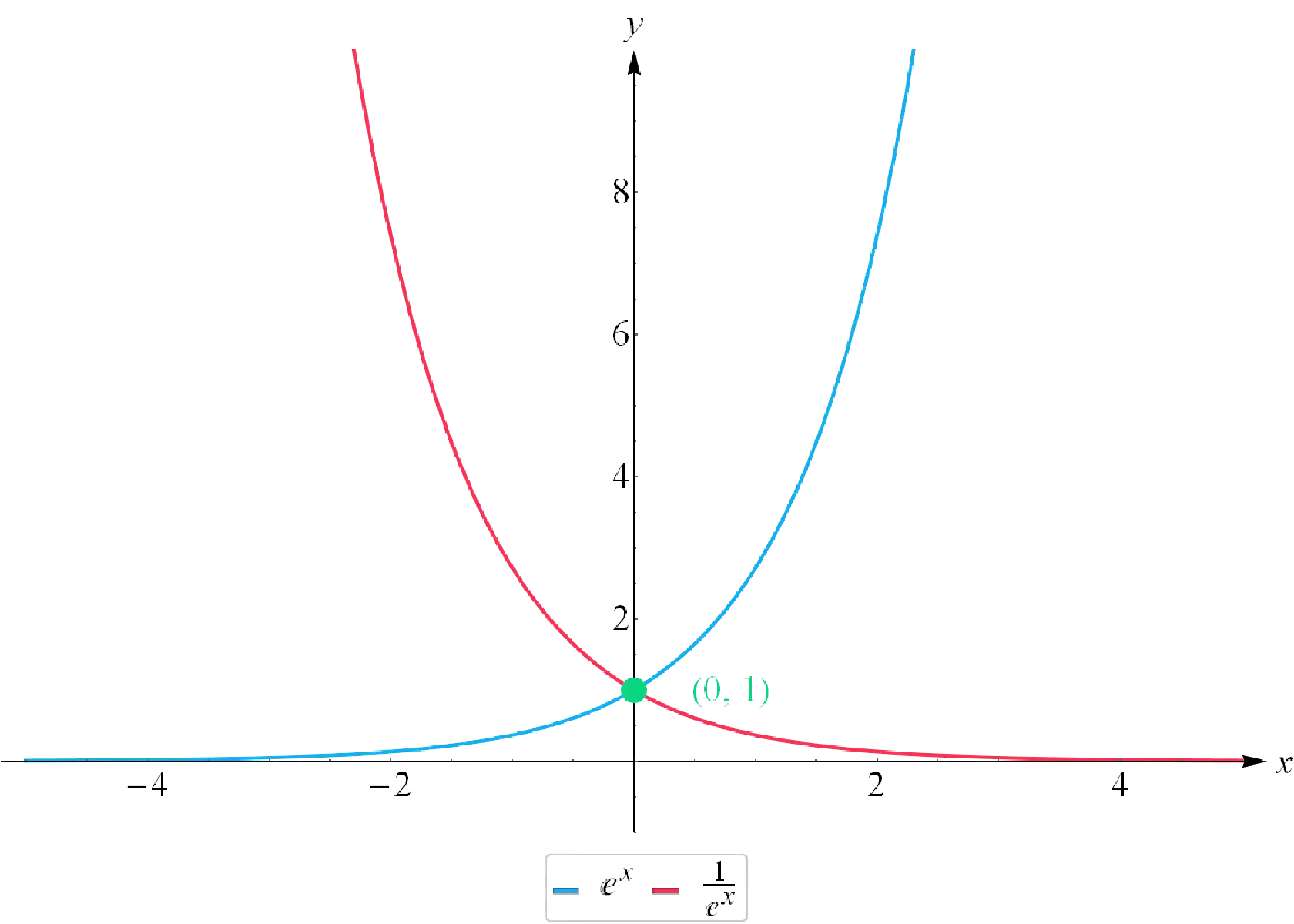
Una funzione esponenziale è definita come una funzione in cui la base è costante e l’esponente è variabile. Nel contesto specifico della funzione esponenziale con base il numero di Nepero, essa viene espressa come f(x) = ex. In generale, una funzione esponenziale può essere scritta come y = a^x o f(x) = a^x. Nel caso in cui la base della funzione esponenziale è maggiore di 1, essa viene rappresentata graficamente e ha alcune proprietà ben definite.

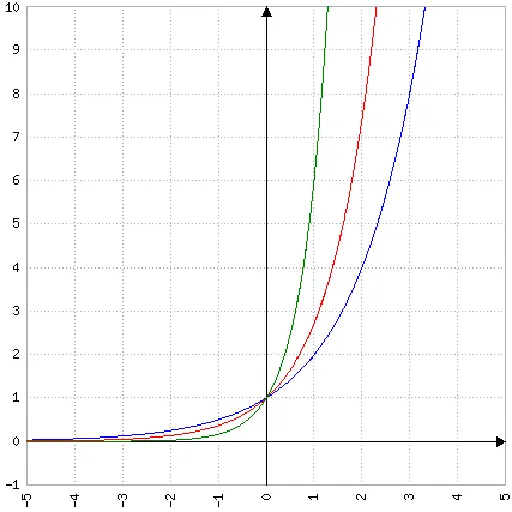
È importante sottolineare che nel caso specifico della funzione esponenziale con base e, essa viene indicata come y = e^x o f(x) = e^x. In questo contesto, il grafico della funzione esponenziale con base maggiore di 1 è crescente e asintotico all’asse delle ascisse, con l’intercetta sull’asse delle ordinate in corrispondenza del punto (0,1). La funzione presenta inoltre una serie di proprietà, tra cui la simmetria rispetto alla bisettrice dei quadranti e l’essere sempre positiva.
Grafico della funzione esponenziale
Proprietà della funzione esponenziale
La funzione esponenziale con base maggiore di 1 presenta numerose proprietà interessanti, che la rendono molto utile in molte applicazioni matematiche e scientifiche. Di seguito, vediamo le principali proprietà analitiche della funzione esponenziale:
Dominio
Il dominio della funzione esponenziale con base maggiore di 1 è l’insieme dei numeri reali, ovvero Dom(f) = (-∞,+∞).
Pari o dispari
La funzione esponenziale non è né pari né dispari.
Limiti
La funzione esponenziale è illimitata superiormente e ha immagine Im(f) = (0,+∞). Inoltre, ai due estremi del dominio, la funzione presenta i seguenti limiti:
- lim_(x → -∞)a^x = 0^+
- lim_(x → +∞)a^x = +∞
Esponenziali : introduzione alla funzione esponenziale e principali caratteristiche – YouTube
Monotonia e convessità
La funzione esponenziale è monotona crescente strettamente su tutto il dominio e convessa su tutto il dominio.
Continuità e derivabilità
La funzione esponenziale è continua su tutto R e derivabile su tutto R.
Derivata
La derivata dell’esponenziale è:
(d)/(dx)a^(x) = a^(x)ln(a)
Integrale
L’integrale dell’esponenziale è:
∫a^(x)dx = (a^(x))/(ln(a))+c
Sviluppo di Taylor
Per studenti universitari, lo sviluppo di Taylor (con centro in x_0 = 0) della funzione y = e^x è:
e^(x) = 1+x+(x^2)/(2)+(x^3)/(6)+(x^4)/(24)+(x^5)/(120)+···+(x^n)/(n!)+o(x^n) ∀ x∈R
Fonte: Wikipedia
Stai guardando: FUNZIONE ESPONENZIALE E^X, A^X