RETTE PARALLELE E PERPENDICOLARI
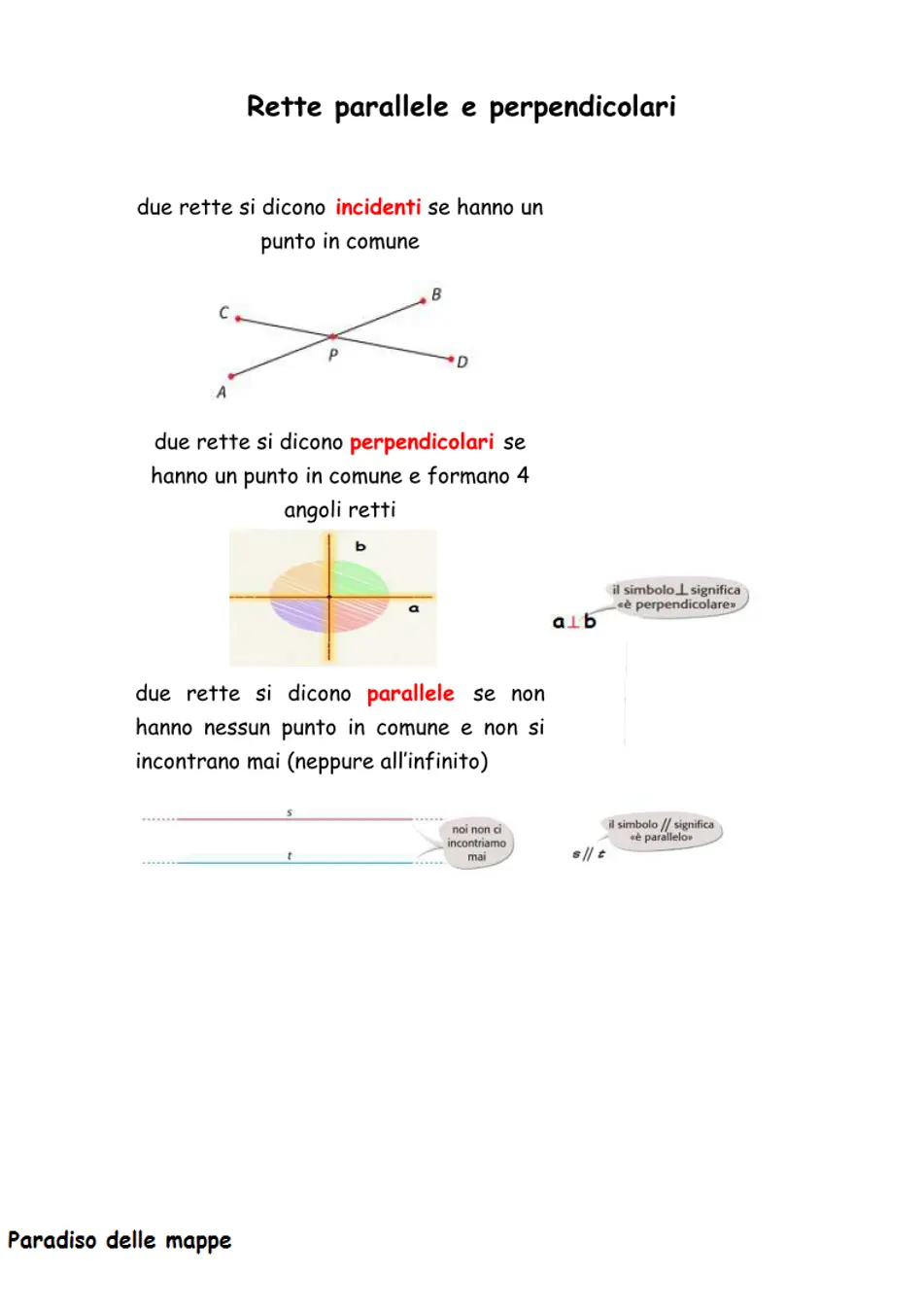
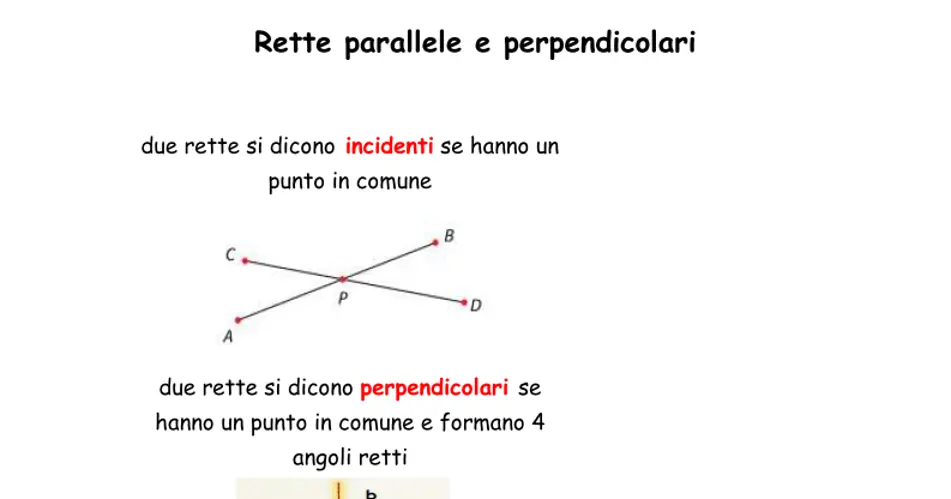
Nel piano cartesiano, due rette parallele non si incontrano mai, mentre due rette perpendicolari si intersecano ad angolo retto. Per determinare se due rette sono parallele o perpendicolari, possiamo utilizzare alcune condizioni e formule specifiche. Nel caso di rette parallele, le equazioni delle due rette hanno lo stesso coefficiente angolare, mentre nel caso di rette perpendicolari il coefficiente angolare di una delle due rette è l’opposto dell’inverso del coefficiente angolare dell’altra retta. Ricordiamo che due rette coincidenti sono sempre parallele e perpendicolari a se stesse. Queste informazioni possono essere utili nella risoluzione di problemi di geometria piana.

Il Coronavirus e la sua diffusione in Italia
Cosa è il Coronavirus?
Il Coronavirus, anche conosciuto come COVID-19, è una malattia infettiva causata dal nuovo virus SARS-CoV-2. Il virus è stato identificato per la prima volta a Wuhan, in Cina, nel dicembre 2019 e si è diffuso rapidamente in tutto il mondo.
Come si diffonde il Coronavirus?
Il Coronavirus si diffonde principalmente attraverso il contatto con goccioline respiratorie di una persona infetta. Queste goccioline possono essere trasmesse da una persona infetta quando tossisce, starnutisce o parla. È anche possibile contrarre il virus toccando una superficie contaminata e poi toccandosi il viso.
La diffusione del Coronavirus in Italia
In Italia, il primo caso di Coronavirus è stato confermato il 31 gennaio 2020. Da allora, il virus si è diffuso rapidamente in tutto il paese, con la Lombardia che è stata la regione più colpita. Il governo italiano ha adottato misure severe per cercare di contenere la diffusione del virus, tra cui il lockdown nazionale e l’obbligo di indossare mascherine in luoghi pubblici.
Si prega di fare attenzione e di seguire le linee guida del governo per proteggere sé stessi e gli altri dal Coronavirus.
Rette parallele e condizione di parallelismo tra rette
Rette Parallele e Perpendicolari – YouTube
Cosa sono le rette parallele?
Le rette parallele sono due o più rette nel piano che non si intersecano in alcun punto o che coincidono tra loro. Le rette parallele possono essere distinte o coincidenti.
Criterio di parallelismo delle rette parallele
Il criterio di parallelismo delle rette parallele, noto anche come teorema delle rette parallele, si riferisce agli angoli formati da due rette parallele tagliate da una trasversale. Esistono diverse caratterizzazioni equivalenti della definizione di rette parallele, ma la più importante ed elementare è quella relativa al criterio di parallelismo.
Condizione di parallelismo tra rette
Le rette nel piano sono parallele se e solo se hanno lo stesso coefficiente angolare. Se le rette sono date in forma esplicita o implicita, la condizione di parallelismo tra le due rette è data dalle seguenti equazioni:
- Esplicita: due rette r e s sono parallele se e solo se i loro coefficienti angolari sono uguali: m1 = m2
- Verticale: due rette verticali sono parallele tra loro per definizione.
- Implicita: due rette r e s sono parallele se e solo se a1b2 = a2b1
Esempi di rette parallele
- Le rette r: y = 3x+6 e s: y = 3x-8 sono parallele perché presentano lo stesso coefficiente angolare: m_r = 3 = m_s.
- Le rette t: -x+2y+1 = 0 e u: -5x+10y = 0 sono parallele, infatti a_1b_2 = (-1)·10 = -10 = (-5)·2 = a_2b_1.
Le rette parallele sono importanti nella geometria e nella matematica, ed è essenziale capire la loro definizione e la condizione di parallelismo tra le rette. Con queste conoscenze, è possibile risolvere problemi che coinvolgono le rette parallele.
Rette perpendicolari e condizione di perpendicolarità
Cosa sono le rette perpendicolari?
Le rette perpendicolari nel piano sono due rette che si intersecano in un solo punto e formano quattro angoli retti, ovvero angoli di 90 gradi. Le rette perpendicolari sono anche chiamate rette ortogonali.
Condizione di perpendicolarità tra rette
In termini analitici, la condizione di perpendicolarità tra due rette r e s è espressa dalla seguente formula: le due rette sono perpendicolari se e solo se il prodotto tra i loro coefficienti angolari è uguale a -1: m_r·m_s = -1.
Se le due rette sono date in forma esplicita, la condizione di perpendicolarità tra le due rette si esprime attraverso il fatto che il coefficiente angolare di una retta è l’opposto del reciproco del coefficiente angolare dell’altra retta: m_r = -(1)/(m_s).
Se le due rette sono date in forma implicita, la condizione di perpendicolarità tra le due rette è data dalla seguente formula: a1a2+b1b2 = 0.
Esempi di rette perpendicolari
- Le rette r: y = -5x+12 e s: y = (x)/(5)-(6)/(7) sono perpendicolari perché m_r·m_s = (-5)·(1)/(5) = -1.
- Le rette t: 4x+3y = 0 e u: -6x+8y+5 = 0 sono perpendicolari, infatti a1a2+b1b2 = 4·(-6)+3·8 = -24+24 = 0.
Fonte: https://www.matematicamente.it/lezioni-di-matematica/algebra/retta/rette-perpendicolari/
Le rette perpendicolari sono importanti nella geometria e nella matematica, e sono spesso utilizzate per risolvere problemi geometrici. Con le conoscenze della definizione e della condizione di perpendicolarità tra le rette, è possibile determinare se due rette sono perpendicolari e trovare l’equazione di una retta perpendicolare ad un’altra data.
Stai guardando: RETTE PARALLELE E PERPENDICOLARI