VALORE ASSOLUTO

Il valore assoluto, noto anche come modulo, è una funzione che restituisce sempre un valore positivo o zero. In particolare, ad un numero negativo viene associato il suo corrispettivo positivo, mentre i numeri positivi vengono lasciati invariati. In questa lezione, esploreremo il concetto di valore assoluto di un numero reale e analizzeremo le sue proprietà.

Successivamente, introdurremo la funzione modulo (o valore assoluto) e ne studieremo le caratteristiche, oltre a tracciare il suo grafico. In questo modo, avrai una comprensione completa della funzione di valore assoluto e del suo utilizzo in matematica.
Definizione di valore assoluto di un numero reale
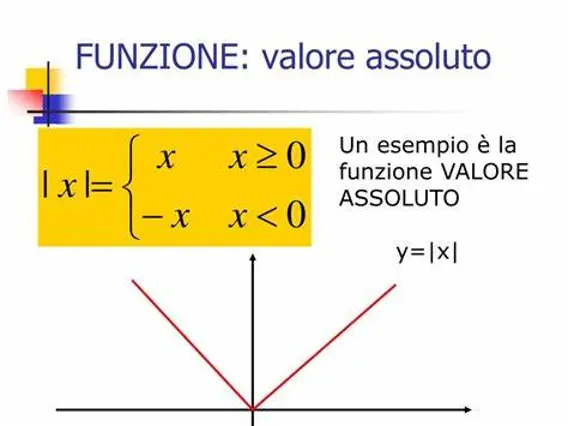
Il valore assoluto di un numero reale x, indicato con |x| o con abs(x), è definito nel modo seguente:
- |x| = x se x è un numero non negativo (cioè positivo o nullo)
- |x| = -x se x è un numero negativo
In notazione matematica:
|x| = x se x ≥ 0; -x se x < 0
Ad esempio, il valore assoluto di -5 è uguale a 5 e si scrive:
|-5| = 5
Il valore assoluto sia di 3/2 che di -3/2 è uguale a 3/2:
|(3)/(2)| = (3)/(2) ; |-(3)/(2)| = (3)/(2)
Il valore assoluto di qualsiasi numero reale è sempre un numero non negativo.
Equazioni con Valore Assoluto – YouTube
Proprietà del valore assoluto di un numero reale
Siano a e b due numeri reali. Di seguito, sono elencate le proprietà del valore assoluto:
- Il valore assoluto di a è una quantità maggiore o uguale a zero. In notazione matematica:
- Il valore assoluto di a è uguale a zero se e solo se a è uguale a zero. In notazione matematica:
- Il valore assoluto di un prodotto è uguale al prodotto dei valori assoluti:
- Supponendo che b sia diverso da zero, il valore assoluto di a fratto b è uguale al rapporto dei valori assoluti:
- Il valore assoluto di una differenza è uguale a zero se e solo se minuendo e sottraendo sono uguali:
- In notazione matematica:
- In notazione matematica:
- Disuguaglianza triangolare:
- Lipschitzianità del valore assoluto:
Funzione valore assoluto o funzione modulo
Il valore assoluto di un numero reale x è una funzione che associa ad x un numero reale non negativo (|x|). La definizione matematica è la seguente:
| |: R → R, x ↦ |x|: = x se x ≥ 0 ;-x se x < 0
Proprietà del valore assoluto (o modulo):
Il dominio del valore assoluto è (-∞,+∞). La funzione è pari e ha un’immagine Im(f) = [0,+∞) illimitata superiormente. Inoltre, il valore assoluto è monotono, ovvero è strettamente decrescente per x < 0 e strettamente crescente per x > 0. È anche convessa su tutto R e continua su tutto R, ad eccezione del punto angoloso in x=0.
Il limite del valore assoluto agli estremi del dominio è:
| x | → +∞ per x → ±∞
La derivata del valore assoluto è:
|x|’ = x/|x| per x≠0
Mentre l’integrale del valore assoluto è:
∫ |x| dx = x |x|/2 + C
Fonte: YouMath
Stai guardando: VALORE ASSOLUTO