ARCOTANGENTE ARCTAN(X)
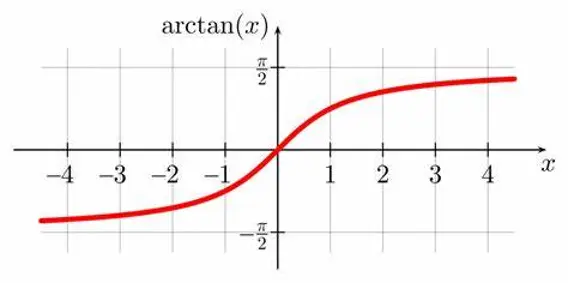
La funzione goniometrica inversa arcotangente, indicata con arctan(x), arctg(x) o atan(x), rappresenta l’inversa della funzione tangente e restituisce gli angoli in radianti compresi tra -∏/2 e +∏/2. La funzione arcotangente y=arctan(x) può essere rappresentata graficamente e possiede diverse proprietà che possono essere facilmente consultate in un formulario. La sua equazione è f(x) = arctan(x).

La definizione e il calcolo dell’arcotangente
Definizione
L’arcotangente è definita come la funzione inversa della tangente sull’intervallo $(-\frac{\pi}{2}, \frac{\pi}{2})$. In altre parole, fissato $x \in \mathbb{R}$, l’angolo $\alpha = \arctan(x)$ è l’angolo compreso tra $-\frac{\pi}{2}$ e $\frac{\pi}{2}$ tale che $\tan(\alpha) = x$.
Calcolo
Per calcolare l’arcotangente di un valore $x$, dobbiamo trovare l’angolo $\alpha$ compreso tra $-\frac{\pi}{2}$ e $\frac{\pi}{2}$ tale che $\tan(\alpha) = x$. Questo può essere fatto utilizzando la definizione stessa dell’arcotangente.
Ad esempio, per calcolare $\arctan(1)$, dobbiamo trovare l’angolo $\alpha$ tale che $\tan(\alpha) = 1$. Osservando la tabella dei valori delle funzioni goniometriche, vediamo che $\tan(\frac{\pi}{4}) = 1$. Poiché $\frac{\pi}{4}$ è compreso tra $-\frac{\pi}{2}$ e $\frac{\pi}{2}$, abbiamo che $\arctan(1) = \frac{\pi}{4}$.
Grafico
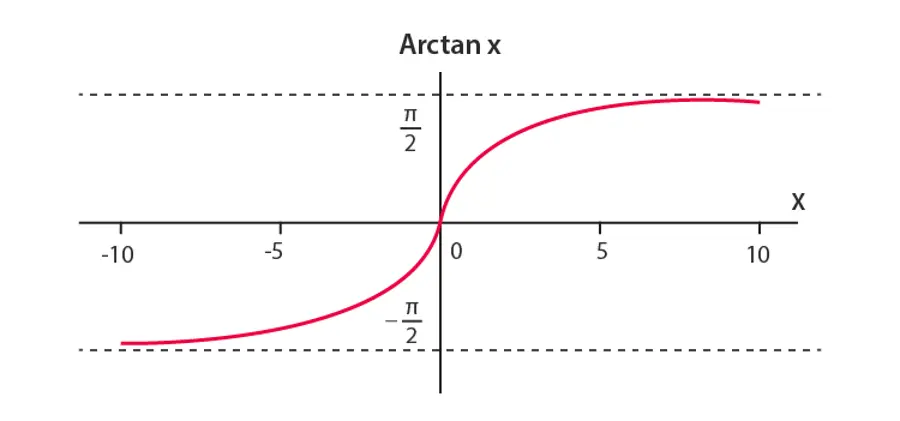
Il grafico dell’arcotangente è una curva che si estende su tutto l’intervallo $(-\infty, \infty)$ e ha asintoti verticali in corrispondenza di $x = -\frac{\pi}{2}$ e $x = \frac{\pi}{2}$.
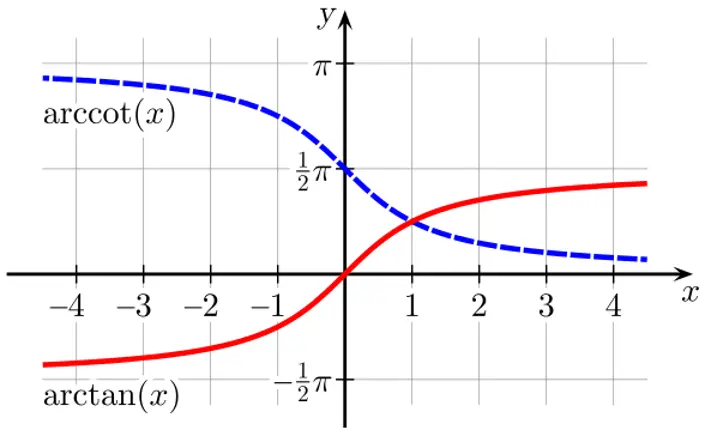
Identità dell’arcotangente
Prima di iniziare a utilizzare l’arcotangente per risolvere esercizi, è utile conoscere alcune identità che possono semplificare i calcoli. Ecco le principali identità dell’arcotangente:
Seno de arcotangente de x. Sen(arctan x) – YouTube
Identità di base
- $\arctan(\tan(x)) = x$ per $-\frac{\pi}{2} < x < \frac{\pi}{2}$
- $\tan(\arctan(x)) = x$ per ogni $x \in \mathbb{R}$
Identità trigonometriche
- $\sin(\arctan(x)) = \frac{x}{\sqrt{1+x^2}}$ (Dimostrazione: sin(arctan(x)))
- $\cos(\arctan(x)) = \frac{1}{\sqrt{1+x^2}}$
- $\cot(\arctan(x)) = \frac{1}{x}$ per $x \neq 0$
- $\sec(\arctan(x)) = \sqrt{x^2+1}$
- $\csc(\arctan(x)) = \frac{\sqrt{x^2+1}}{x}$ per $x \neq 0$
Identità di somma
- $\arctan(x)+\operatorname{arccot}(x) = \frac{\pi}{2}$ per ogni $x$
- $\arctan(x)+\arctan\left(\frac{1}{x}\right) = \begin{cases} -\frac{\pi}{2} & \text{se } x < 0 \ \frac{\pi}{2} & \text{se } x > 0 \end{cases}$ per $x \neq 0$
Le identità dell’arcotangente possono essere utili per semplificare i calcoli e risolvere alcuni esercizi di trigonometria. Per ulteriori formule trigonometriche, si può consultare la lezione dedicata.
Fonte: Matematicamente.it.
Proprietà dell’arcotangente
1) Dominio
Il dominio dell’arcotangente è $(-\infty,+\infty)$.
2) Parità
L’arcotangente è una funzione dispari, ovvero $\operatorname{arctan}(-x) = -\operatorname{arctan}(x)$ per ogni $x$.
3) Immagine
L’arcotangente è una funzione limitata, con immagine nell’intervallo $(-\frac{\pi}{2},\frac{\pi}{2})$.
4) Monotonia
L’arcotangente è una funzione monotona strettamente crescente su tutto il dominio.
5) Convessità
L’arcotangente è concava sull’intervallo $(0,+\infty)$ e convessa sull’intervallo $(-\infty,0)$.
6) Continuità e derivabilità
L’arcotangente è continua su tutto $\mathbb{R}$ e derivabile su tutto $\mathbb{R}$.
7) Limiti
Gli estremi del dominio dell’arcotangente hanno limiti finiti:
$$\lim_{x \to -\infty} \operatorname{arctan}(x) = -\frac{\pi}{2} \quad \text{e} \quad \lim_{x \to +\infty} \operatorname{arctan}(x) = \frac{\pi}{2}$$
8) Limite notevole
L’arcotangente ha il seguente limite notevole:
$$\lim_{x \to 0} \frac{\operatorname{arctan}(x)}{x} = 1$$
9) Derivata
La derivata dell’arcotangente è:
$$\frac{d}{dx}\operatorname{arctan}(x) = \frac{1}{1+x^2}$$
10) Integrale
L’integrale dell’arcotangente è:
$$\int \operatorname{arctan}(x)dx = x\operatorname{arctan}(x) – \frac{1}{2}\log(x^2+1) + C$$
11) Sviluppo di Taylor
Lo sviluppo di Taylor dell’arcotangente con centro in $x_0 = 0$ è:
$$\operatorname{arctan}(x) = x – \frac{x^3}{3} + \frac{x^5}{5} – \frac{x^7}{7} + \frac{x^9}{9} + o(x^9)$$
Queste proprietà dell’arcotangente possono essere utili nella risoluzione di problemi di matematica e analisi.
Fonte: Matematika.it.
Stai guardando: ARCOTANGENTE ARCTAN(X)