TRIANGOLO RETTANGOLO
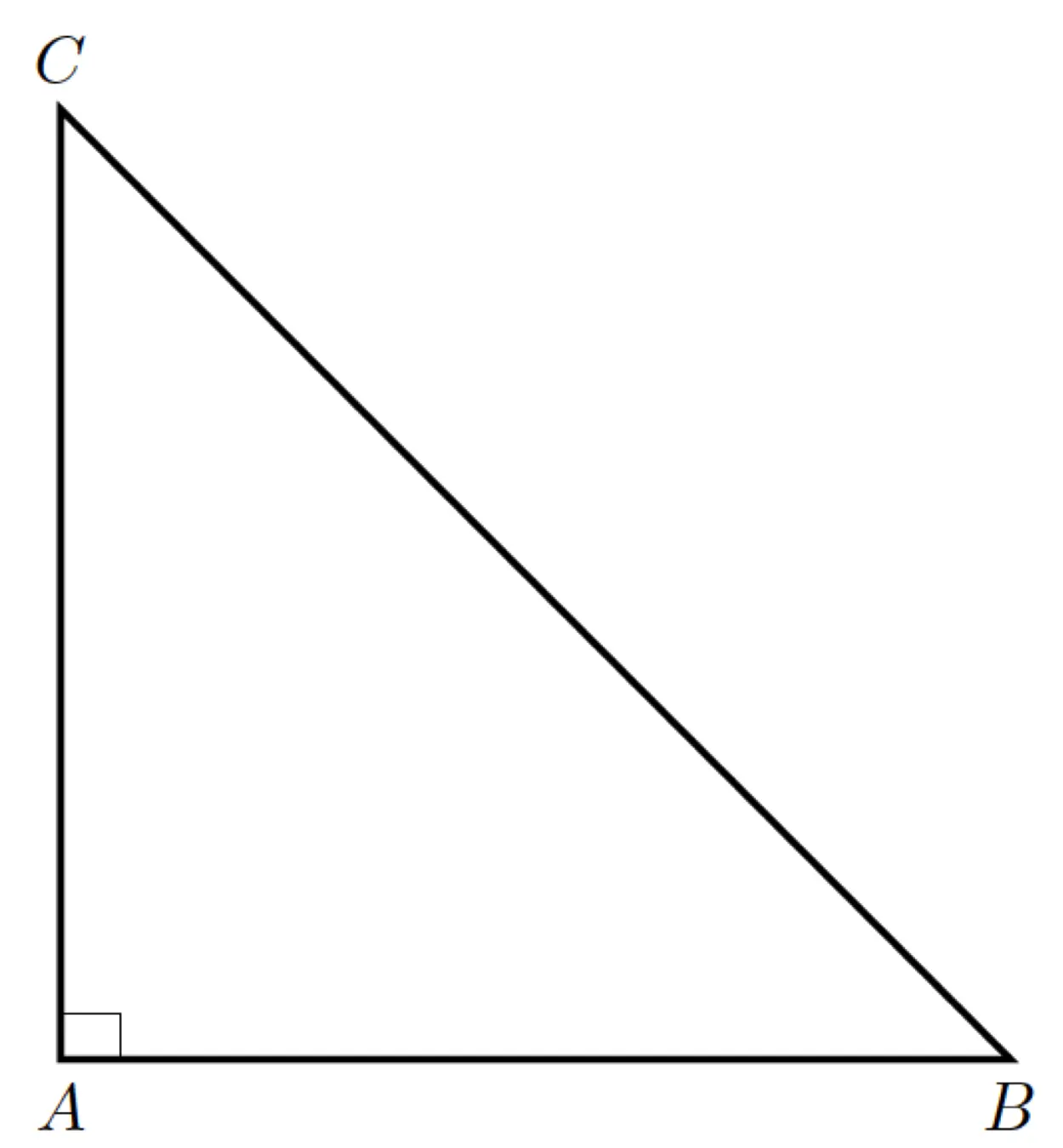
Un triangolo rettangolo è un tipo di triangolo in cui uno degli angoli interni misura esattamente 90°, ed è chiamato angolo retto. I due lati che formano l’angolo retto sono detti cateti, mentre il lato opposto all’angolo retto è chiamato ipotenusa. Il triangolo rettangolo è importante in matematica perché ci sono molte formule utili per risolvere i problemi relativi ad esso.

Ad esempio, ci sono formule per trovare l’area, l’altezza e il perimetro del triangolo rettangolo, nonché formule basate sul teorema di Pitagora e sui teoremi di Euclide. Ci sono anche formule specifiche per i triangoli rettangoli particolari, come il triangolo rettangolo isoscele (45°-45°) e quello con angoli acuti di 30°-60°. Inoltre, ci sono molte proprietà dei triangoli rettangoli, inclusi i teoremi più importanti. Infine, ci sono esempi di esercizi e problemi svolti relativi ai triangoli rettangoli.
Triangolo rettangolo: definizione e formule
Definizione di triangolo rettangolo
Un triangolo rettangolo è un triangolo che possiede un angolo retto, ovvero un angolo di 90 gradi, o due lati perpendicolari tra loro. Questa definizione è alla base della classificazione dei triangoli in base agli angoli.
Formule del triangolo rettangolo
Per calcolare diverse grandezze di un triangolo rettangolo, possiamo utilizzare le seguenti formule:
Perimetro del triangolo rettangolo
Il perimetro di un triangolo rettangolo è dato dalla somma dei tre lati:
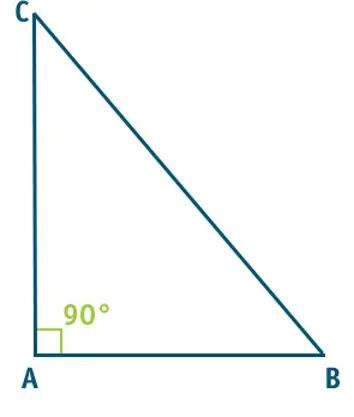
2p = i+c1+c2
Trigonometria: teoremi sui Triangoli Rettangoli e loro risoluzione – YouTube
Ipotenusa
L’ipotenusa di un triangolo rettangolo può essere calcolata come:
i = 2p-c1-c2
Cateto minore e maggiore
I cateti minore e maggiore possono essere calcolati come segue:
c1 = 2p-i-c2
c2 = 2p-i-c1
Area del triangolo rettangolo
L’area del triangolo rettangolo può essere calcolata come il semiprodotto dei due cateti diviso due:
S = (c1×c2)/(2)
Altre formule utili
È possibile calcolare le grandezze del triangolo rettangolo utilizzando anche le seguenti formule:
- Altezza relativa all’ipotenusa:
h = (c1×c2)/(i)
- Altezza dal semiperimetro:
h = (2S)/(i)
- Altezza dal prodotto tra l’ipotenusa e l’altezza:
h = (i×h)/(2)
- Ipotenusa dal teorema di Pitagora:
i = √(c1^2+c2^2)
- Cateto minore dal teorema di Pitagora:
c1 = √(i^2-c2^2)
- Cateto maggiore dal teorema di Pitagora:
c2 = √(i^2-c1^2)
- Altezza dal primo teorema di Euclide:
h = √(p1×p2)
- Proiezione del cateto maggiore sull’ipotenusa dal secondo teorema di Euclide:
p2 = (c2^2)/(i)
- Proiezione del cateto minore sull’ipotenusa dal secondo teorema di Euclide:
p1 = (c1^2)/(i)
Triangolo rettangolo is
Proprietà del triangolo rettangolo
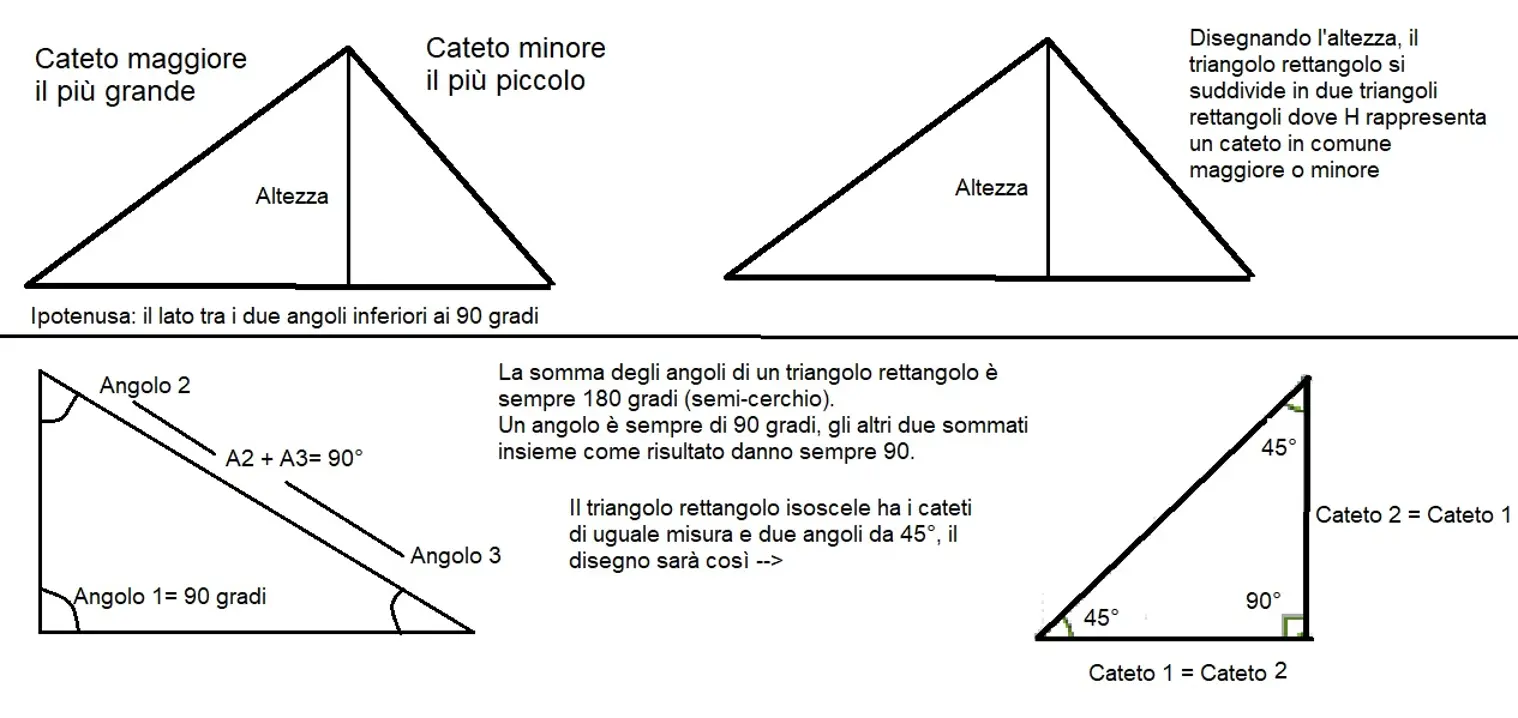
Definizione di triangolo rettangolo
Un triangolo rettangolo è un tipo di triangolo che possiede un angolo interno pari a 90°, dunque due lati perpendicolari tra loro. Il lato opposto all’angolo retto si chiama ipotenusa, mentre gli altri due lati si chiamano cateti.
Proprietà del triangolo rettangolo
Angoli interni e complementari
Gli angoli interni diversi dall’angolo retto sono angoli acuti e sono complementari. Ciò è dovuto al fatto che la somma degli angoli interni di un triangolo qualsiasi vale 180°, e poiché c’è un angolo di 90°, la somma delle ampiezze degli altri due angoli è necessariamente pari a 90°.
Ortocentro
L’ortocentro di un triangolo rettangolo coincide con il vertice dell’angolo retto.
Circoncentro e semicirconferenza circoscritta
Un triangolo rettangolo è sempre inscrivibile in una semicirconferenza. Il circocentro coincide con il punto medio dell’ipotenusa, che a sua volta coincide con il diametro della semicirconferenza circoscritta.
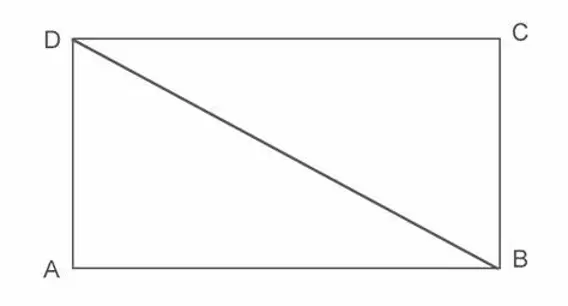
Metà di un rettangolo
Un triangolo rettangolo è metà di un determinato rettangolo.
Altezza relativa ai cateti
Ciascun cateto è l’altezza relativa all’altro cateto.
Mediana relativa all’ipotenusa
In ogni triangolo rettangolo la mediana relativa all’ipotenusa è metà dell’ipotenusa stessa.
Teorema di Pitagora
Vale il teorema di Pitagora: in un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui due cateti.
i^2 = c1^2+c2^2
Primo teorema di Euclide
Vale il primo teorema di Euclide: in un triangolo rettangolo ciascun cateto è il medio proporzionale tra l’ipotenusa e la proiezione del cateto sull’ipotenusa.
i:c1 = c1:p1 ; i:c2 = c2:p2
Secondo teorema di Euclide
Vale il secondo teorema di Euclide: in un triangolo rettangolo l’altezza relativa all’ipotenusa è il medio proporzionale tra le proiezioni dei due cateti sull’ipotenusa.
p1:h = h:p2
Per maggiori informazioni sui teoremi di Euclide, si rimanda alla lezione specifica.
Fonte: <a href=”https://it.wikipedia.org/wiki/Triangolo_rettang
Triangoli rettangoli con coppie di angoli notevoli (triangoli rettangoli notevoli)
Triangolo rettangolo isoscele (45°-45°)
In un triangolo rettangolo isoscele con angoli acuti di 45°-45°, i due cateti sono congruenti. Se chiamiamo la loro misura comune c = c_1 = c_2, vale la seguente relazione tra la loro misura e la misura dell’ipotenusa:
i = c√(2) ; c = (i)/(√(2))
Triangolo rettangolo 30°-60°
In un triangolo rettangolo con angoli acuti di 30°-60°, il cateto minore c_1 si oppone all’angolo minore di ampiezza 30°, mentre il cateto maggiore c_2 si oppone all’angolo maggiore di ampiezza 60°. Valgono le seguenti relazioni tra le misure dei cateti e dell’ipotenusa:
- Cateto minore (dal cateto maggiore): c_1 = (c_2)/(√(3))
- Cateto maggiore (dal cateto minore): c_2 = c_1√(3)
- Ipotenusa (dal cateto minore): i = 2c_1
- Ipotenusa (dal cateto maggiore): i = (2)/(√(3))c_2
- Cateto minore (dall’ipotenusa): c_1 = (i)/(2)
- Cateto maggiore (dall’ipotenusa): c_2 = (i√(3))/(2)
Fonte: Wikipedia – Triangolo rettangolare
Stai guardando: TRIANGOLO RETTANGOLO