FORMULE TRIGONOMETRICHE

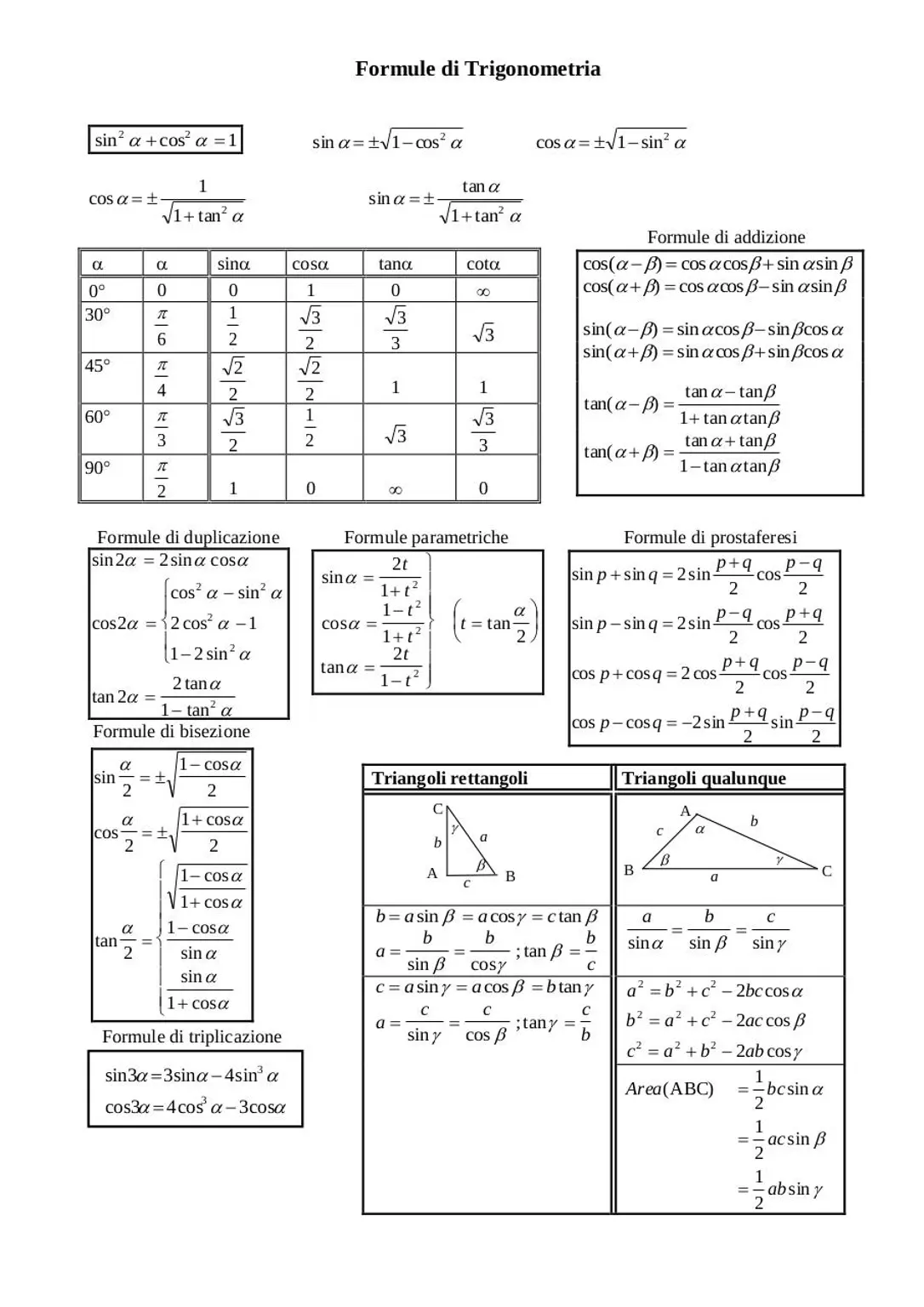
Il seguente formulario riassume le principali formule trigonometriche, che comprendono l’identità fondamentale della Trigonometria, le formule di bisezione e di duplicazione, le formule di Werner, le formule di Prostaferesi e le formule parametriche per seno, coseno e tangente. L’utilizzo di questo formulario può risultare utile in diverse applicazioni pratiche che coinvolgono la Trigonometria.

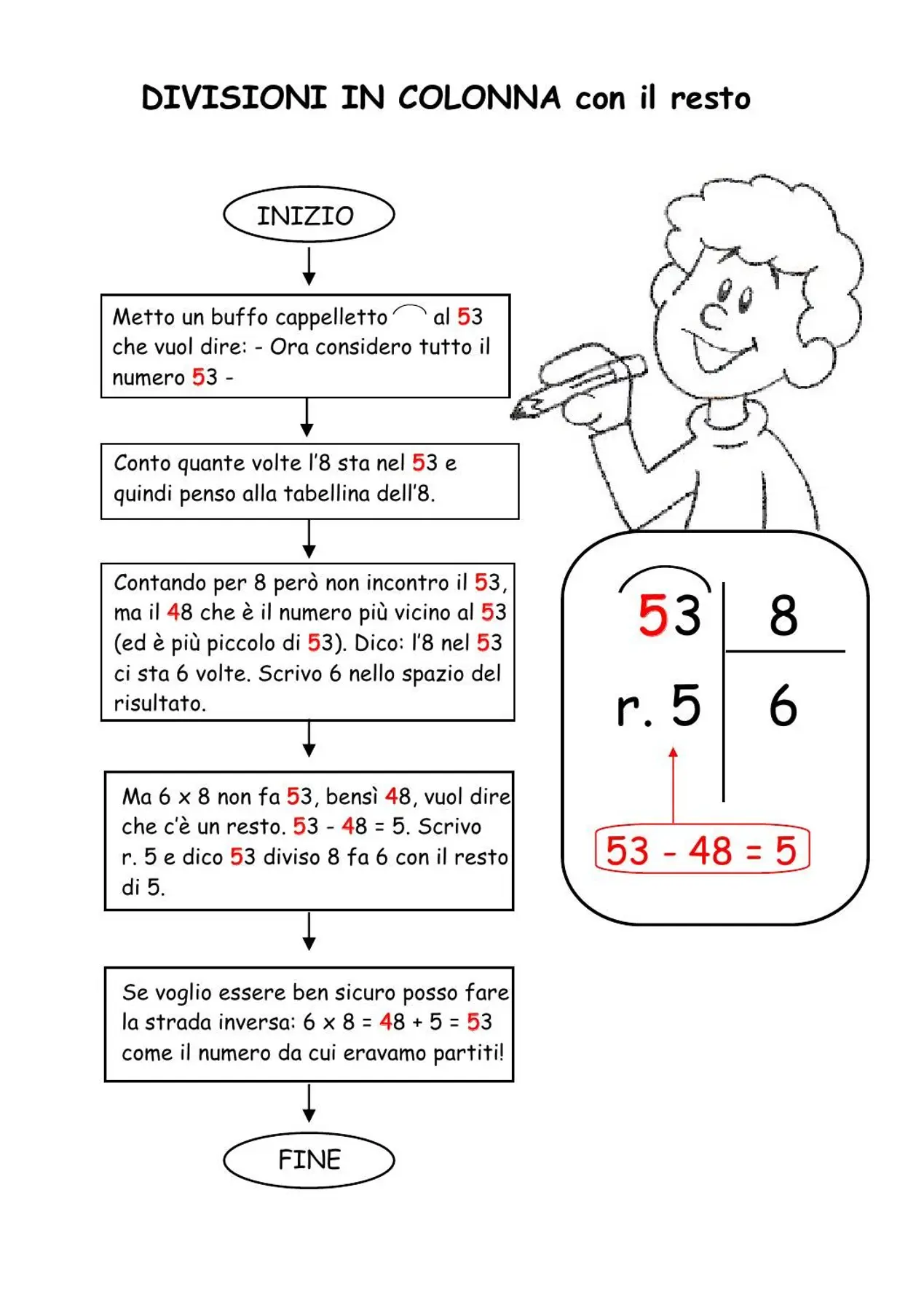
Le principali formule trigonometriche

In matematica, le formule trigonometriche sono delle relazioni che riguardano le funzioni trigonometriche. Le formule trigonometriche sono ampiamente utilizzate in geometria, fisica e ingegneria. Qui di seguito sono elencate le formule trigonometriche più importanti:

Identità fondamentale della trigonometria

L’identità fondamentale della trigonometria è una delle formule più importanti della trigonometria. Essa permette di riscrivere il seno in funzione del coseno e viceversa.

sin²(α) + cos²(α) = 1

È possibile utilizzare questa formula in due diverse forme:

• sin²(α) = 1 – cos²(α)
• cos²(α) = 1 – sin²(α)

Formule per gli archi associati per seno e coseno

Le formule sugli angoli associati consentono di calcolare il valore di seno e coseno di particolari angoli, chiamati archi associati. Di seguito sono elencati i valori di seno e coseno degli archi associati:

• sin((π/2)-α) = cos(α); cos((π/2)-α) = sin(α)
• sin((π/2)+α) = cos(α); cos((π/2)+α) = -sin(α)
• sin(π-α) = sin(α); cos(π-α) = -cos(α)
• sin(π+α) = -sin(α); cos(π+α) = -cos(α)
• sin((3/2)π-α) = -cos(α); cos((3/2)π-α) = -sin(α)
• sin((3/2)π+α) = -cos(α); cos((3/2)π+α) = sin(α)
• sin(-α) = -sin(α); cos(-α) = cos(α)

Fonte: https://www.matematika.it/formule-trigonometriche.html

Formule di Addizione, Sottrazione, Duplicazione & Co in goniometria 😉 – YouTube

Formule trigonometriche avanzate

Formule di sommazione degli angoli per seno, coseno, tangente

Le formule di sommazione degli angoli per seno, coseno e tangente permettono di riscrivere le funzioni goniometriche applicate alla somma o alla differenza di due angoli, in modo da disaccoppiare gli angoli. Di seguito sono riportate le formule di sommazione per seno, coseno e tangente:

• sin(α+β) = sin(α)cos(β) + cos(α)sin(β)
• sin(α-β) = sin(α)cos(β) – cos(α)sin(β)
• cos(α+β) = cos(α)cos(β) – sin(α)sin(β)
• cos(α-β) = cos(α)cos(β) + sin(α)sin(β)
• tan(α+β) = (tan(α)+tan(β))/(1-tan(α)tan(β)) dove α, β, α+β ≠ (π/2)+kπ, k ∈ Z
• tan(α-β) = (tan(α)-tan(β))/(1+tan(α)tan(β)) dove α, β, α-β ≠ (π/2)+kπ, k ∈ Z

Formule di duplicazione

Le formule di duplicazione permettono di esprimere le funzioni trigonometriche applicate al doppio di un angolo in modo alternativo. Di seguito sono riportate le formule di duplicazione:

• sin(2α) = 2sin(α)cos(α)
• cos(2α) = cos²(α) – sin²(α)
• tan(2α) = (2tan(α))/(1-tan²(α)) dove α ≠ (π/4)+k(π/2) ∧ α ≠ (π/2)+kπ, k ∈ Z

Formule parametriche per funzioni trigonometriche

Le formule parametriche sono fondamentali nella risoluzione di equazioni e disequazioni trigonometriche e in esercizi più avanzati. Di seguito sono riportate le formule parametriche per le funzioni trigonometriche:

• sin(α) = (2t)/(1+t²) dove t = tan(α/2) e α ≠ π+2kπ
• cos(α) = (1-t²)/(1+t²) dove t = tan(α/2) e α ≠ π+2kπ
• tan(α) = (2t)/(1-t²) dove t = tan(α/2) e α ≠ (π/2)+kπ ∧ α ≠ π+2kπ
• sin(α)sin(β) = (1/2)[cos(α-β)-cos(α+β)]
• cos(α)cos(β) = (1/2)[cos(α-β)+cos(α+β)]
• sin(α)cos(β) = (1/2)[sin(α-β)+sin(α+β)]
• sin(α)+sin(β) = 2sin((α+β)/2)cos((α-β)/2)
• sin(α)-sin(β) = 2cos((α+β)/2)sin((α-β)/2)
• cos(α)+cos(β) = 2cos((α+β)/2)cos((α-β)/2)
• cos(α)-cos(β) = -2sin((α+β)/2)sin((α-β)/2)

Stai guardando: FORMULE TRIGONOMETRICHE