IPERBOLE E IPERBOLE EQUILATERA
L’iperbole in Geometria Analitica è una conica e rappresenta il luogo geometrico dei punti del piano la cui differenza delle distanze dai due punti fissi, noti come fuochi, è costante. Un’iperbole equilatera ha gli asintoti perpendicolari coincidenti con gli assi. Questo formulario presenta le principali formule dell’iperbole e dell’iperbole equilatera nel piano cartesiano, incluso il calcolo delle coordinate dei fuochi, delle equazioni degli asintoti e dell’eccentricità. Tali formule sono essenziali per comprendere e risolvere i problemi relativi alle iperboli.

Iperbole nel piano cartesiano
L’iperbole è un luogo geometrico dei punti del piano, in cui la differenza delle distanze da due punti fissi, chiamati fuochi, è costante. Questa definizione può essere tradotta in termini algebrici, considerando un generico punto dell’iperbole e imponendo la condizione |PF1 – PF2| = costante.
Un’iperbole è caratterizzata da due assi di simmetria perpendicolari tra loro, e può essere rappresentata da due curve, chiamate rami dell’iperbole. Gli assi dell’iperbole sono le rette rispetto alle quali l’iperbole viene suddivisa in due parti uguali e simmetriche. La semidistanza tra i due rami dell’iperbole è chiamata semiasse trasverso, mentre i vertici dell’iperbole sono i punti di intersezione con uno dei due assi. Il centro dell’iperbole è il punto di intersezione degli assi e corrisponde al centro di simmetria dell’iperbole.
I fuochi dell’iperbole sono i due punti fissi rispetto ai quali è costante la differenza delle distanze da ogni punto dell’iperbole, e appartengono sempre all’asse che interseca l’iperbole. La semidistanza focale è la distanza tra i due fuochi dell’iperbole.
L’iperbole ha inoltre due asintoti, che sono le rette cui si approssimano i rami dell’iperbole all’infinito e che passano per il suo centro. L’eccentricità dell’iperbole è un valore che esprime la deformazione dell’iperbole rispetto agli assi, e misura quanto l’iperbole è schiacciata rispetto ad essi.
Formule dell’iperbole
Iperbole con assi di simmetria coincidenti con gli assi cartesiani
Per l’iperbole con gli assi di simmetria coincidenti con gli assi cartesiani e che interseca l’asse delle ascisse, l’equazione in forma canonica è data da (x^2)/(a^2)-(y^2)/(b^2) = 1, dove a e b sono i semiassi dell’iperbole e a ≠ 0, b ≠ 0. Questa equazione viene talvolta chiamata equazione dell’iperbole riferita ai propri assi.
L’equazione dell’iperbole è quadratica (di grado 2) nelle incognite x,y e ha senso soltanto se i coefficienti a,b sono entrambi non nulli. Un punto P = (x,y) appartiene all’iperbole se e solo se le sue coordinate ne soddisfano l’equazione.
Le radici dei denominatori presenti nell’equazione, a e b, corrispondono alle misure dei semiassi dell’iperbole. L’asse trasverso è l’asse che congiunge i due vertici dell’iperbole. Nel caso di un’iperbole che interseca l’asse x il semiasse trasverso è orizzontale e misura a. L’asse trasverso misura 2a e, se l’iperbole ha il centro nell’origine, è situato sull’asse delle ascisse.
Anche se a^2 ⋛ b^2, l’equazione individua sempre un’iperbole che interseca l’asse delle ascisse ed in cui l’asse trasverso giace sull’asse x. Nel caso particolare a = b si dice parla di iperbole equilatera, che è per definizione un’iperbole con i semiassi congruenti.
Iperbole Equilatera e Iperbole Traslata – YouTube
Iperbole con centro nell’origine
Se l’iperbole ha il centro nell’origine, le formule per il calcolo degli assi e dei semiassi dell’iperbole sono:
- semiasse orizzontale = a
- semiasse verticale = b
- asse orizzontale = 2a
- asse verticale = 2b
Vertici, fuochi, semidistanza focale, asintoti ed eccentricità dell’iperbole
Vertici dell’iperbole
Per un’iperbole che interseca l’asse x con centro nell’origine i vertici sono situati sull’asse x e hanno coordinate V_1 = (-a,0) e V_2 = (+a,0).
Fuochi dell’iperbole
I fuochi di un’iperbole che interseca l’asse x e con centro nell’origine giacciono sull’asse x e hanno coordinate F_1 = (-c,0) e F_2 = (+c,0), dove c = √(a^2+b^2).
Semidistanza focale
L’asse focale di un’iperbole che interseca l’asse x e con centro nell’origine è la retta che congiunge i due fuochi. La semidistanza focale è metà della distanza tra i due fuochi e si calcola mediante la formula c = √(a^2+b^2).
Asintoti dell’iperbole
Le equazioni degli asintoti di un’iperbole che interseca l’asse delle ascisse e con centro nell’origine sono date da y = ±(b)/(a)x. Gli asintoti sono rette passanti per l’origine.
Eccentricità dell’iperbole
L’eccentricità dell’iperbole, che misura la deformazione dell’iperbole rispetto agli assi, è definita come il rapporto tra la semidistanza focale e la lunghezza del semiasse trasverso. Nel caso di un’iperbole che interseca l’asse x e con centro nell’origine, la formula per calcolarla è e = (c)/(a), dove c = √(a^2+b^2). L’eccentricità dell’iperbole è sempre maggiore di 1: e > 1. Al tendere di e → 1, l’iperbole si schiaccia sempre di più sull’asse delle ascisse, mentre per valori crescenti di e si approssima all’asse delle ordinate.
Fonte: YouMath
Iperbole traslata che interseca l’asse delle x
Un’iperbole che interseca l’asse delle x e con il centro C = (xC,yC) non nell’origine costituisce una generalizzazione del caso appena visto e presenta un’equazione della forma:
((x-xC)2)/(a2) – ((y-yC)2)/(b2) = 1
In questo caso gli assi dell’iperbole sono rette parallele agli assi cartesiani ed hanno equazioni:
x = xC ; y = yC
Rispetto al caso dell’iperbole che interseca l’asse x con centro nell’origine restano invariate le formule per semidistanza focale ed eccentricità. Il semiasse trasverso coincide ancora con il semiasse orizzontale e misura a; il semiasse non trasverso è ancora quello verticale e misura b.
Le coordinate dei vertici e quelle dei fuochi possono essere ricavate con una semplice traslazione e applicando le corrispondenti formule di cambiamento delle coordinate:
V1 = (xC-a,yC) ; V2 = (xC+a,yC) ; F1 = (xC-c,yC) ; F2 = (xC+c,yC)
Per le equazioni degli asintoti basta ricorrere all’equazione della retta passante per un punto:
(y-yC) = ±(b)/(a)(x-xC)
Formule dell’iperbole
In questo articolo si descrivono le formule principali dell’iperbole con assi di simmetria paralleli agli assi cartesiani. Si distinguono due casi: iperbole che interseca l’asse x con centro nell’origine e traslata; iperbole che interseca l’asse y con centro nell’origine e traslata.
Iperbole che interseca l’asse delle x con centro nell’origine
L’equazione dell’iperbole è data da:
(x^2)/(a^2)-(y^2)/(b^2) = 1
Le radici dei denominatori a, b corrispondono alle misure dei semiassi dell’iperbole. L’asse trasverso misura 2a e l’asse non trasverso misura 2b. Il semiasse trasverso è orizzontale e misura a. I vertici dell’iperbole hanno coordinate V1 = (-a, 0) e V2 = (+a, 0). I fuochi dell’iperbole hanno coordinate F1 = (-c, 0) e F2 = (+c, 0), dove c = √(a^2+b^2) è la semidistanza focale. Le equazioni degli asintoti dell’iperbole sono y = ±(b)/(a)x. L’eccentricità dell’iperbole è e = c/a = √(a^2+b^2)/a.
Iperbole traslata che interseca l’asse delle x
L’equazione dell’iperbole traslata con centro C = (x_C,y_C) non nell’origine è:
((x-x_C)^2)/(a^2)-((y-y_C)^2)/(b^2) = 1
Le coordinate dei vertici e dei fuochi possono essere ricavate con le formule V1 = (x_C-a, y_C), V2 = (x_C+a, y_C), F1 = (x_C-c, y_C) e F2 = (x_C+c, y_C). Gli assi dell’iperbole sono rette parallele agli assi cartesiani e le equazioni sono x = x_C e y = y_C. Il semiasse trasverso è orizzontale e misura a; il semiasse non trasverso è verticale e misura b. Le equazioni degli asintoti dell’iperbole sono y – y_C = ±(b)/(a)(x – x_C).
Iperbole che interseca l’asse delle y con centro nell’origine
L’equazione dell’iperbole è data da:
(x^2)/(a^2)-(y^2)/(b^2) = -1
L’asse trasverso è verticale e misura 2b. L’asse non trasverso è orizzontale e misura 2a. Il semiasse trasverso è verticale e misura b. I vertici dell’iperbole hanno coordinate V1 = (0, -b) e V2 = (0, +b). I fuochi dell’iperbole hanno coordinate F1 = (0, -c) e F
Iperbole traslata che interseca l’asse y
Un’iperbole che interseca l’asse delle ordinate e ha il centro C = (xC,yC) non nell’origine, presenta un’equazione della forma:
((x-xC)2)/(a2) – ((y-yC)2)/(b2) = -1
Gli assi dell’iperbole sono rette parallele agli assi cartesiani ed hanno equazioni:
x = xC ; y = yC
Le formule per semidistanza focale ed eccentricità sono sempre le stesse. Il semiasse trasverso coincide ancora con il semiasse verticale e misura b; il semiasse non trasverso è orizzontale e misura a.
Per le coordinate dei vertici e dei fuochi basta ragionare per traslazione:
V1 = (xC,yC-b) ; V2 = (xC,yC>+b) ; F1 = (xC,yC>-c) ; F2 = (xC,yC>+c)
Per le equazioni degli asintoti possiamo usare l’equazione della retta passante per un punto:
(y-yC) = ±(b)/(a)(x-xC)
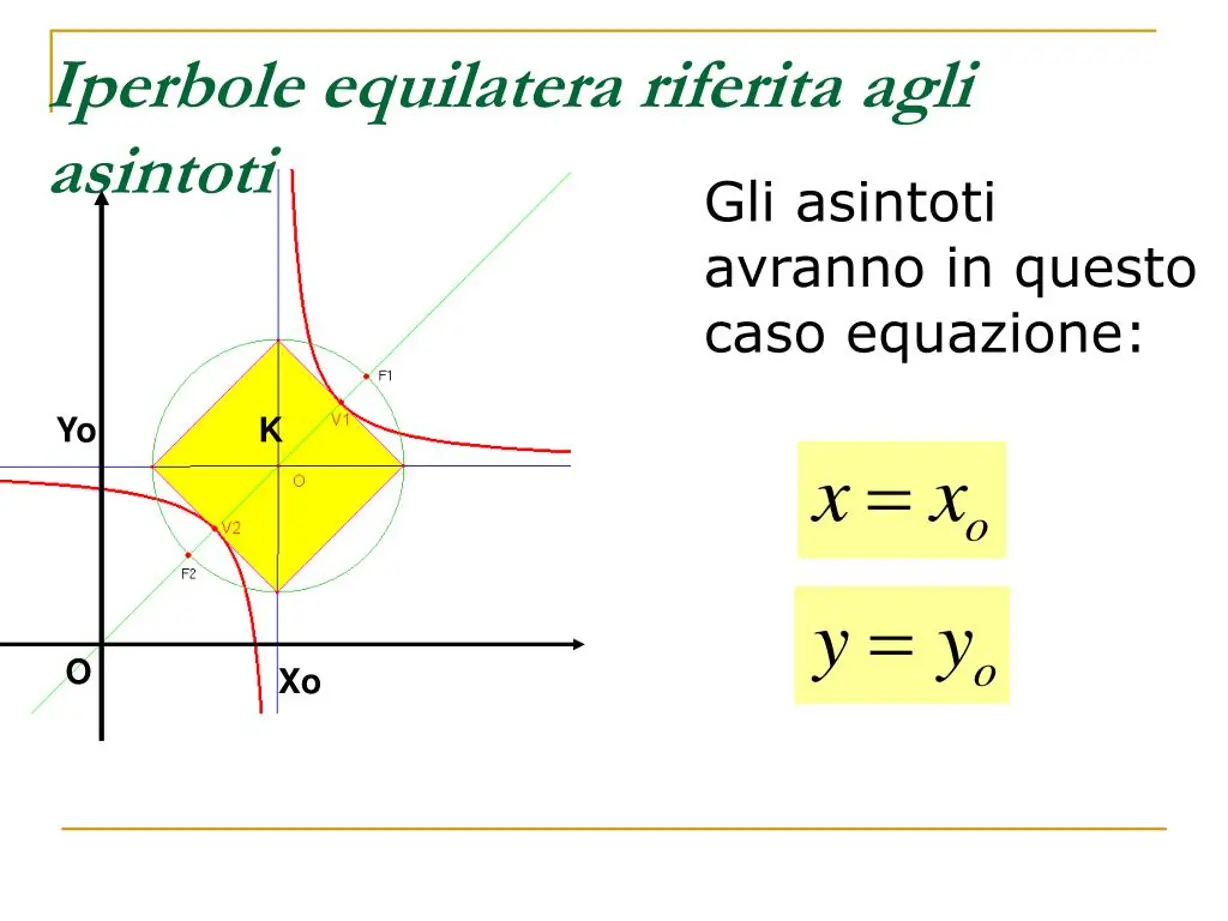
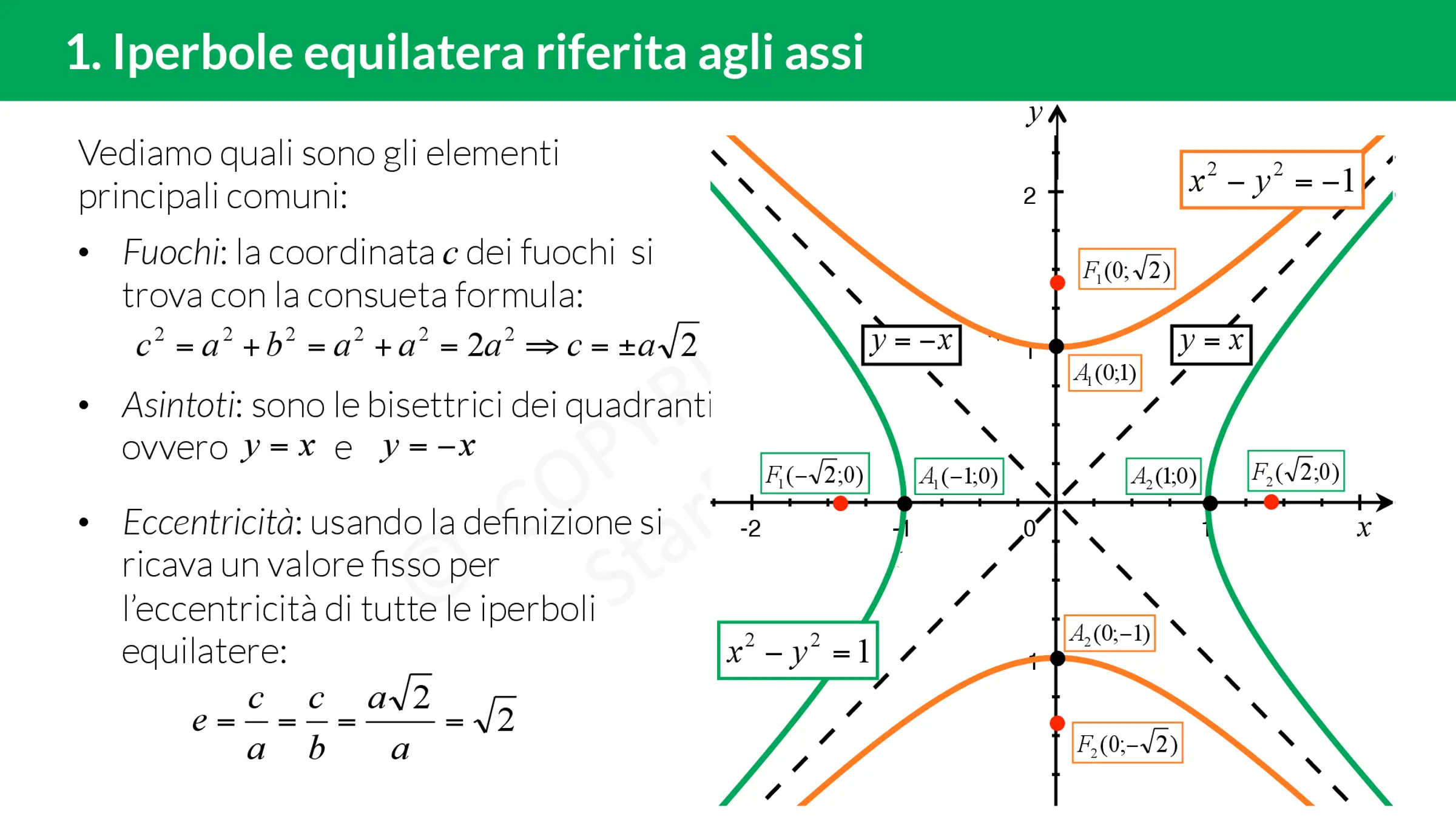
Iperbole equilatera riferita ai propri asintoti
Un’iperbole equilatera è un’iperbole in cui le misure dei semiassi coincidono, ossia a = b. Se consideriamo il centro nell’origine degli assi, può presentarsi con un’equazione della forma:
x2 – y2 = a2 ; x2 – y2 = -a2
Dalle formule degli asintoti si capisce subito che un’iperbole equilatera ha gli asintoti perpendicolari, poiché a = b, e dunque otteniamo i coefficienti angolari m = ±1. Possiamo allora decidere di considerare il piano cartesiano scegliendo come assi gli asintoti dell’iperbole equilatera. In questo contesto si parla di iperbole equilatera riferita ai propri asintoti.
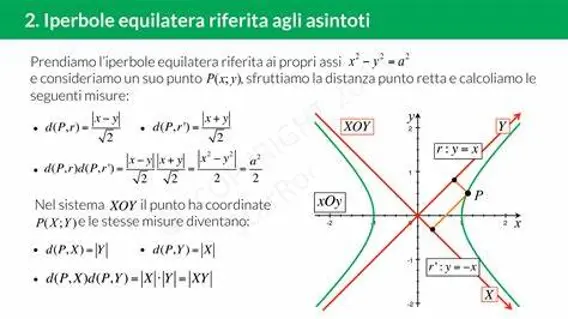
Iperbole equilatera riferita ai propri asintoti
L’iperbole equilatera è un tipo particolare di iperbole in cui i due semiassi hanno la stessa misura, ovvero $a=b$. Quando l’iperbole equilatera è riferita ai propri asintoti, la sua equazione assume la forma $xy=k$, con $k\neq 0$.
Il centro di un’iperbole equilatera riferita ai propri asintoti si trova sempre nell’origine degli assi. Gli assi di simmetria sono dati dalle due bisettrici dei quattro quadranti.
Coordinate dei fuochi
I fuochi dell’iperbole equilatera riferita ai propri asintoti hanno coordinate date da:
- $F_1 = (-\sqrt{2k}, -\sqrt{2k})$ e $F_2 = (\sqrt{2k}, \sqrt{2k})$ se $k > 0$;
- $F_1 = (-\sqrt{-2k}, \sqrt{-2k})$ e $F_2 = (\sqrt{-2k}, -\sqrt{-2k})$ se $k < 0$.
Per calcolare la semidistanza focale dell’iperbole equilatera riferita ai propri asintoti, si può usare la formula:
$$\text{semidistanza focale} = 2\sqrt{|k|}$$
Coordinate dei vertici
I vertici dell’iperbole equilatera riferita ai propri asintoti hanno coordinate date da:
- $A_1 = (-\sqrt{k}, -\sqrt{k})$ e $A_2 = (\sqrt{k}, \sqrt{k})$ se $k > 0$;
- $A_1 = (-\sqrt{-k}, \sqrt{-k})$ e $A_2 = (\sqrt{-k}, -\sqrt{-k})$ se $k < 0$.
Semiasse trasverso
La lunghezza del semiasse trasverso dell’iperbole equilatera riferita ai propri asintoti è data dalla formula:
$$\text{semiasse trasverso} = \sqrt{2|k|}$$
Fonte del contenuto: matematika.it
Stai guardando: IPERBOLE E IPERBOLE EQUILATERA